A pulsar is a rapidly rotating neutron star, the result of the gravitational collapse of an ordinary star that has used up its fuel supply. A certain pulsar has a rotational period of T=0.033sec and radius R=1/38km. The tangential speed of a point on the equator is ___________(km/s)
To find the tangential speed of a point on the equator of the pulsar, we can follow these steps:
1. Identify the given values:
- Rotational period T=0.033 seconds
- Radius R=138 km
2. Convert the radius from kilometers to meters:
R=138 km=138×1000 m=100038 m≈26.32 m
3. Calculate the angular speed ω:
The angular speed ω is given by the formula:
ω=2πT
Substituting the value of T:
ω=2π0.033 rad/s
4. Calculate ω:
ω≈6.28320.033≈190.44 rad/s
5. Calculate the tangential speed v:
The tangential speed v is given by:
v=ωR
Substituting the values of ω and R:
v≈190.44×26.32 m/s
6. Calculate v:
v≈5000.00 m/s
7. Convert v to kilometers per second:
v≈5000.001000 km/s=5.00 km/s
Final Answer:
The tangential speed of a point on the equator of the pulsar is approximately 5.00 km/s.
- Rotational period T=0.033 seconds
- Radius R=138 km
R=138 km=138×1000 m=100038 m≈26.32 m
The angular speed ω is given by the formula:
ω=2πT
Substituting the value of T:
ω=2π0.033 rad/s
ω≈6.28320.033≈190.44 rad/s
The tangential speed v is given by:
v=ωR
Substituting the values of ω and R:
v≈190.44×26.32 m/s
v≈5000.00 m/s
v≈5000.001000 km/s=5.00 km/s
The tangential speed of a point on the equator of the pulsar is approximately 5.00 km/s.
Similar Questions
A thin taut string tied at both ends and oscillating in its third harmonic has its shape described by the equation y(x,t)=(5.60cm)sin[(0.0340radcm)x]sin[(50.0rads)t], where the origin is at the left end of the string, the x-axis is along the string and the y-axis is perpendicular to the string.
(a) Draw a sketch that shows the standing wave pattern.
(b)Find the amplitude of the two travelling waves that make up this standing wave.
(c) What is the length of the string?
(d) Find the wavelength, frequency, period and speed of the travelling wave.
(e) Find the maximum transverse speed of a point on the string.
(f) What would be the equation y(x,t) for this string if it were vibrating in its eighth harmonic?View SolutionSuppose the earth increases its speed of rotation . At what new time period will the weightof a body on the equator becomes zero? Take g=10ms2 and radius of the earth R=6400km.
View Solution
Knowledge Check
- Question 1 - Select One
Certain extremely dense neutron stars are believed to be rotating at about 1 rev/sec. If such a star has a radius of 20 km, the acceleration of an object in m//sec^(2) on the equator of the star will be
A8×105B20×103C12×106D4×108
A small bead of mass m = 1 kg is free to move on a circular hoop. The circular hoop has centre at C and radius r = 1 m and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop, at the position shown in figure is : (Take g=10m/s2)
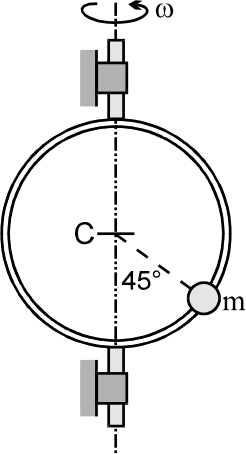 View Solution
View SolutionThe mass ofa star is 3.98×1030 kg and its radius is 106 km. It rotates.about its axis with an angular speed of 10−6 rad/s. Calculate the speed of the star when it collapses to a radius of 104 km ? Assume the moment of inertia of the star to be 25mr2.
View SolutionIf the earth has no rotational motion, the weight of a person on the equation is W. Detrmine the speed with which the earth would have to rotate about its axis so that the person at the equator will weight 34 W. Radius of the earth is 6400 km and g = 10 m/s2.
View SolutionIf the earth has no rotational motion, the weight of a person on the equation is W. Detrmine the speed with which the earth would have to rotate about its axis so that the person at the equator will weight 34 W. Radius of the earth is 6400 km and g = 10 m/s2.
View SolutionA particle is revolving in a circle of radius 1 m with an angular speed of 12 rad/s. At t = 0, it was subjected to a constant angular acceleration α and its angular speed increased to (480π) rotation per minute (rpm) in 2 sec. Particle then continues to move with attained speed. Calculate
(i) angular acceleration of the particle,
(ii) tangential velocity of the particle as a function of time.
(iii) acceleration of the particle at t = 0.5 second and at t = 3 second
(iv) angular displacement at t = 3 second.View SolutionRutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:

(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If an object of mass 2 kg and constant b=4N−sm has terminal speed vT in a liquid then time required to reach 0.63vT from start of the motion is :View Solution

