A particle P is initially at a distance c'=16m from a fixed point O. The particle P moves with a velocity →v=5∧PO+3ˆi. Where ∧PO is a unit vector from P to O at any time t. Initially ∧PO is perpendicular to ˆi. Find the time in seconds after which point P meets point O.
To solve the problem, we need to analyze the motion of the particle P as it moves towards the fixed point O. Let's break down the steps to find the time after which point P meets point O.
1. Understanding the Initial Setup:
- The particle P is initially at a distance of c'=16m from point O.
- The velocity of the particle is given by:
\(
\vec{v} = 5 \hat{PO} + 3 \hat{i}
\)
- Here, ˆPO is a unit vector pointing from P to O, and initially, ˆPO is perpendicular to ˆi (the x-axis).
2. Breaking Down the Velocity:
- The velocity has two components:
- A component of 5 directed towards O (along ˆPO).
- A constant component of 3 in the positive x-direction (along ˆi).
3. Effective Velocity Towards O:
- As the particle moves, the angle θ between the line PO and the x-axis changes. The effective velocity towards O can be expressed as:
\(
v_{\text{effective}} = 5 - 3 \cos(\theta)
\)
- Here, 3cos(θ) is the component of the x-direction velocity along the line PO.
4. Setting Up the Equation:
- The total distance d covered by the particle P towards O must equal the initial distance of 16m. Therefore, we can write:
\(
16 = \int_0^t (5 - 3 \cos(\theta)) dt
\)
5. Finding the x-component Displacement:
- The net displacement in the x-direction is zero since the particle starts at (0,16) and ends at (0,0). Thus:
\(
0 = 3t - \int_0^t 5 \cos(\theta) dt
\)
- Rearranging gives:
\(
\int_0^t \cos(\theta) dt = \frac{3t}{5}
\)
6. Substituting Back:
- Substitute the integral of cos(θ) back into the distance equation:
\(
16 = 5t - 3 \left(\frac{3t}{5}\right)
\)
- Simplifying:
\(
16 = 5t - \frac{9t}{5}
\)
\(
16 = \frac{25t - 9t}{5}
\)
\(
16 = \frac{16t}{5}
\)
7. Solving for Time t:
- Multiply both sides by 5:
\(
80 = 16t
\)
- Divide by 16:
\(
t = 5 \text{ seconds}
\)
Final Answer:
The time after which point P meets point O is 5 seconds.
- The particle P is initially at a distance of c'=16m from point O.
- The velocity of the particle is given by:
\(
\vec{v} = 5 \hat{PO} + 3 \hat{i}
\)
- Here, ˆPO is a unit vector pointing from P to O, and initially, ˆPO is perpendicular to ˆi (the x-axis).
- The velocity has two components:
- A component of 5 directed towards O (along ˆPO).
- A constant component of 3 in the positive x-direction (along ˆi).
- As the particle moves, the angle θ between the line PO and the x-axis changes. The effective velocity towards O can be expressed as:
\(
v_{\text{effective}} = 5 - 3 \cos(\theta)
\)
- Here, 3cos(θ) is the component of the x-direction velocity along the line PO.
- The total distance d covered by the particle P towards O must equal the initial distance of 16m. Therefore, we can write:
\(
16 = \int_0^t (5 - 3 \cos(\theta)) dt
\)
- The net displacement in the x-direction is zero since the particle starts at (0,16) and ends at (0,0). Thus:
\(
0 = 3t - \int_0^t 5 \cos(\theta) dt
\)
- Rearranging gives:
\(
\int_0^t \cos(\theta) dt = \frac{3t}{5}
\)
- Substitute the integral of cos(θ) back into the distance equation:
\(
16 = 5t - 3 \left(\frac{3t}{5}\right)
\)
- Simplifying:
\(
16 = 5t - \frac{9t}{5}
\)
\(
16 = \frac{25t - 9t}{5}
\)
\(
16 = \frac{16t}{5}
\)
- Multiply both sides by 5:
\(
80 = 16t
\)
- Divide by 16:
\(
t = 5 \text{ seconds}
\)
The time after which point P meets point O is 5 seconds.
Similar Questions
A particle P is moving with a constant speed of 6m/s in a direction 2ˆi−ˆj+2ˆk. When t=0,P is at a point whose position vectors is 3ˆi+4ˆj−7ˆk. Find the position vector of the particle P after 4 seconds.
View SolutionThe period of a particle executing SHM is T. There is a point P at a distance 'x' from the mean position 'O'. When the particle passes P towards OP, it has speed v. Find the time in which it returns to P again.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected at time t=0 from a point P on the ground with a speed v0, at an angle of 45∘ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem t=v0/g
Aa. mv302√2gBb. mv30√2gCc. 3mv30√2gDd. √2mv30g
A particle projected from origin moves in x-y plane with a velocity →v=3ˆi+6xˆj, where ˆi and ˆj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
View SolutionThe position of a particle is expressed as →r=(4t2ˆi+2tˆj) m, where t is time in second. Find the velocity o the particle at t = 3 s
View SolutionA particle is thrown vertically upwards from the surface of the earth. Let TP be the time taken by the particle to travel from a point P above the earth to its highest point and back to the point P. Similarly, let TQ be the time taken by the particle to travel from another point Q above the earth to its highest point and back to the same in terms of TP,TQ and H, is :-
View SolutionA particle is given a horizontal velocity u, from the point P on a smooth horizontal floor which has a vertical circular track at the end. ABC is a semicircular track of radius r in the vertical plane. If the path length PA is x=3r and the particle returns to point P, then the initial speed of the particle is
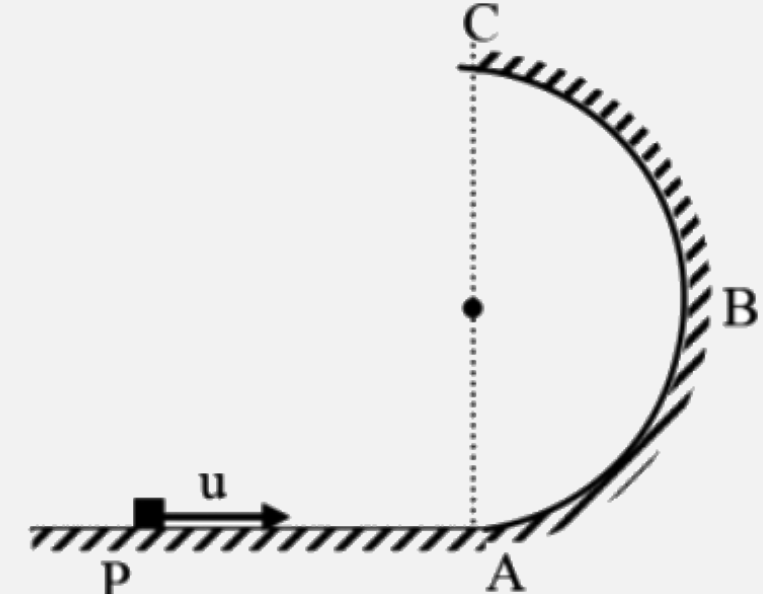 View Solution
View SolutionA particle A moves with velocity (2ˆi−3ˆj)m/s from a point (4,5m)m. At the same instant a particle B, moving in the same plane with velocity(4ˆi+ˆj)m/s passes through a point C(0,−3)m. Find the x-coordinate (in m) of the point where the particles collide.
View Solution
A particle of charge 'q' and mass 'm' enters a uniform magnetic field region →B=−Bˆk at origin 'O' with a velocity →v0=6ˆi m/s and after some time it exist the magentic field region with a velocity →v=(3ˆi+3√3)m/s as shown. The time interval for which the particle has moved in the magnetic field region isView SolutionTwo particles P and Q are moving with velocity of (ˆi+ˆj) and (−ˆi+2ˆj) respectively. At time t=0, P is at origin and Q is at a point with positive vector (2ˆi+ˆj). Then the shortest distance between P & Q is :-
View Solution

