If there is a moth sitting at point C of rolling sphere, where velocity of the centre of mass =v, calculate the velocity of the moth as seen by an oberver sitting at point D at this instant
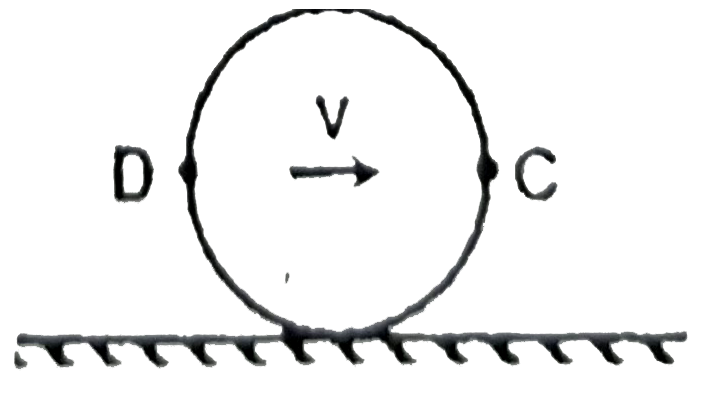
√2v at 45∘ to the horizontal
2v horizontal
v at 45∘ to horizontal
2v going down
ω=vR
vc.g=vˆi+Rωˆj=vˆi+vˆj
vD.g=vˆi+Rω(−ˆj)=vˆi−vˆj
vC.D=vc.g−vd.g=vˆi+vˆj−vˆi+vˆj=2vˆj

Similar Questions
A disc is rolling the velocity of its centre of mass is Vcm then which one will be correct : -
View SolutionA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is vCM, then true statement is

View SolutionA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is vCM, then true statement is

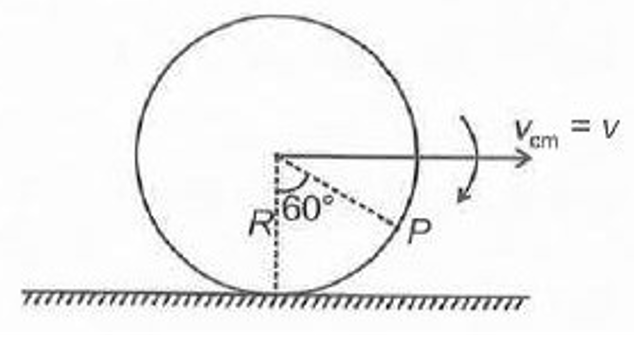
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
View SolutionA solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View Solution
Due to slipping points A and B on the rim of the disk have the velocities shown. Determine the velocities of the centre point C and point F at this instant.
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
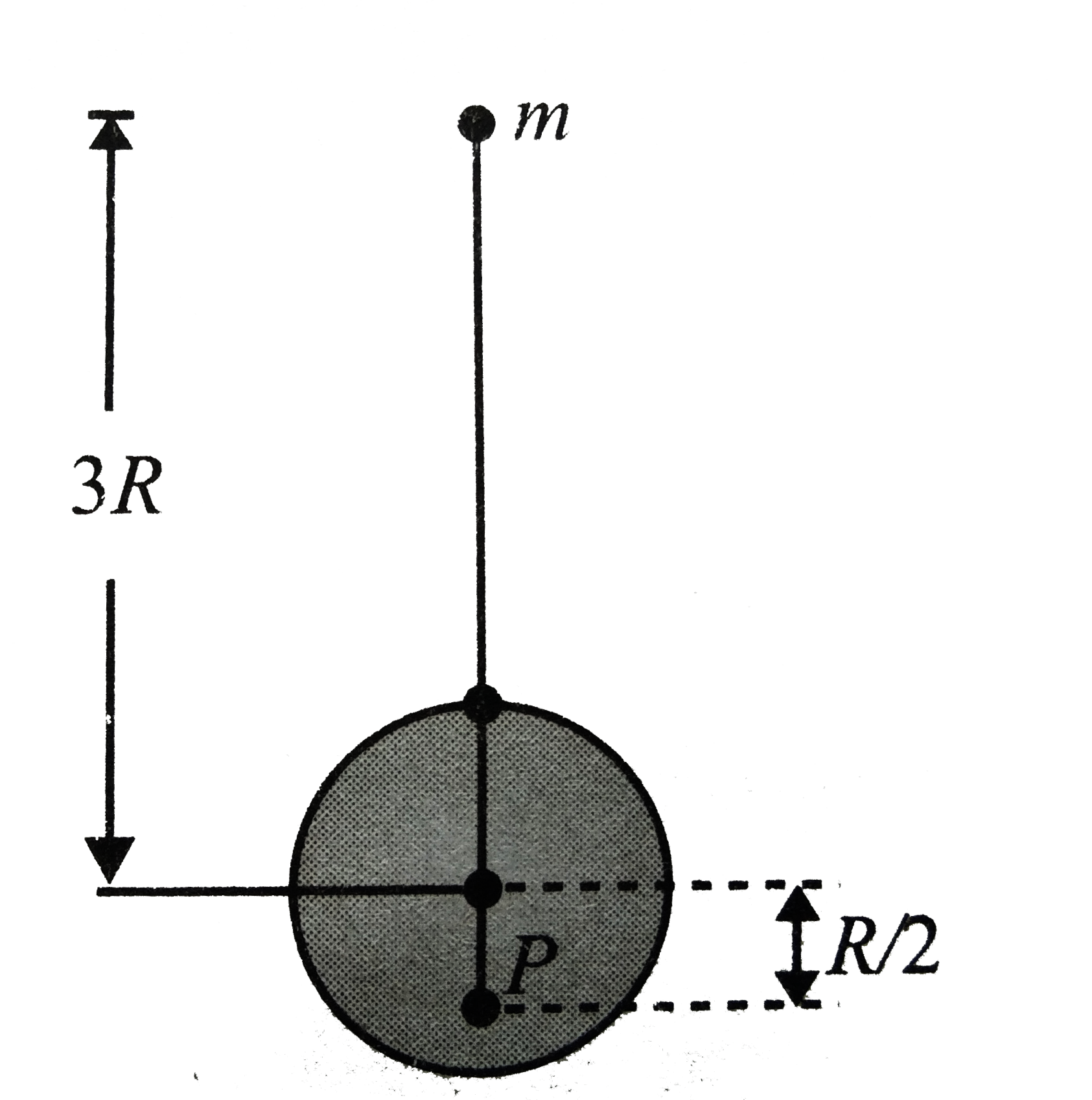
View SolutionA point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
View SolutionA solid cylinder is rolling without slipping with velocity of its centre of mass v and angular velocity about its centre of mass ω on a horizontal frictionless surface as shown in figure. If it collides with a frictionless vertical wall X, then after collision its velocity and angular velocity respectively become

View SolutionA sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.
View Solution
