A non conducting ring of radius R1 is charged such that the linear charge density is λ1cos2θ where θ is the polar angle. If the radius is increased to R2 keeping the charge constant, the linear charge density is changed to λ2cos2θ. The relation connecting R1, R2λ1 and λ2 will be
λ1/R1=λ2/R2
λ1/R2=λ2/R1
λ1λ2=R1R2
λ21R1=λ22R2
To solve the problem, we need to derive a relation connecting the initial radius R1, the new radius R2, the initial linear charge density λ1, and the new linear charge density λ2.
1. Understanding the Charge Distribution:
- The linear charge density on the ring is given as λ1cos2θ for radius R1.
- When the radius changes to R2, the linear charge density changes to λ2cos2θ.
2. Calculating the Total Charge:
- The charge dq on a small segment of the ring can be expressed as:
dq=λ⋅dL
- For a small arc length dL at angle θ, we have:
dL=Rdθ
- Therefore, the charge dq becomes:
dq=λ⋅Rdθ
3. Integrating to Find Total Charge:
- To find the total charge Q on the ring, we integrate dq over the full angle from 0 to 2π:
Q=∫2π0λ⋅Rdθ
- Substituting λ=λ1cos2θ:
Q=∫2π0λ1cos2θ⋅R1dθ
4. Using the Integral of Cosine:
- The integral of cos2θ over one complete cycle is:
∫2π0cos2θdθ=π
- Thus, the total charge Q becomes:
Q=λ1R1⋅π
5. Applying the Same Logic for the New Radius:
- For the new radius R2 and charge density λ2:
Q=λ2R2⋅π
6. Equating the Charges:
- Since the total charge remains constant when the radius changes:
λ1R1⋅π=λ2R2⋅π
- Canceling π from both sides gives:
λ1R1=λ2R2
7. Final Relation:
- Rearranging the equation, we find the relation:
λ1λ2=R2R1
- The linear charge density on the ring is given as λ1cos2θ for radius R1.
- When the radius changes to R2, the linear charge density changes to λ2cos2θ.
- The charge dq on a small segment of the ring can be expressed as:
dq=λ⋅dL
- For a small arc length dL at angle θ, we have:
dL=Rdθ
- Therefore, the charge dq becomes:
dq=λ⋅Rdθ
- To find the total charge Q on the ring, we integrate dq over the full angle from 0 to 2π:
Q=∫2π0λ⋅Rdθ
- Substituting λ=λ1cos2θ:
Q=∫2π0λ1cos2θ⋅R1dθ
- The integral of cos2θ over one complete cycle is:
∫2π0cos2θdθ=π
- Thus, the total charge Q becomes:
Q=λ1R1⋅π
- For the new radius R2 and charge density λ2:
Q=λ2R2⋅π
- Since the total charge remains constant when the radius changes:
λ1R1⋅π=λ2R2⋅π
- Canceling π from both sides gives:
λ1R1=λ2R2
- Rearranging the equation, we find the relation:
λ1λ2=R2R1
Similar Questions
Knowledge Check
An infinite cylinder of radius ro, carrying linear charge density λ. The equation of the equipotential surface for the cylinder is
Ar=r0eπε0[V(r)+V(r0)]λBr=r0e2πε0[V(r)−V(r0)]λ2Cr=r0e−2πε0[V(r)=V(r0)]λDr=r0e−2πε0[V(r)−V(r0)]λ
A ring of radius R carries a non - uniform charge of linear density λ=λ0cosθ sec in the figure) Magnitude of the net dipolement of the ring is :

View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View Solutionthe linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
View SolutionAn arc of radius r carries charge. The linear density of charge is λ and the arc subtends an angle π3 at the centre.
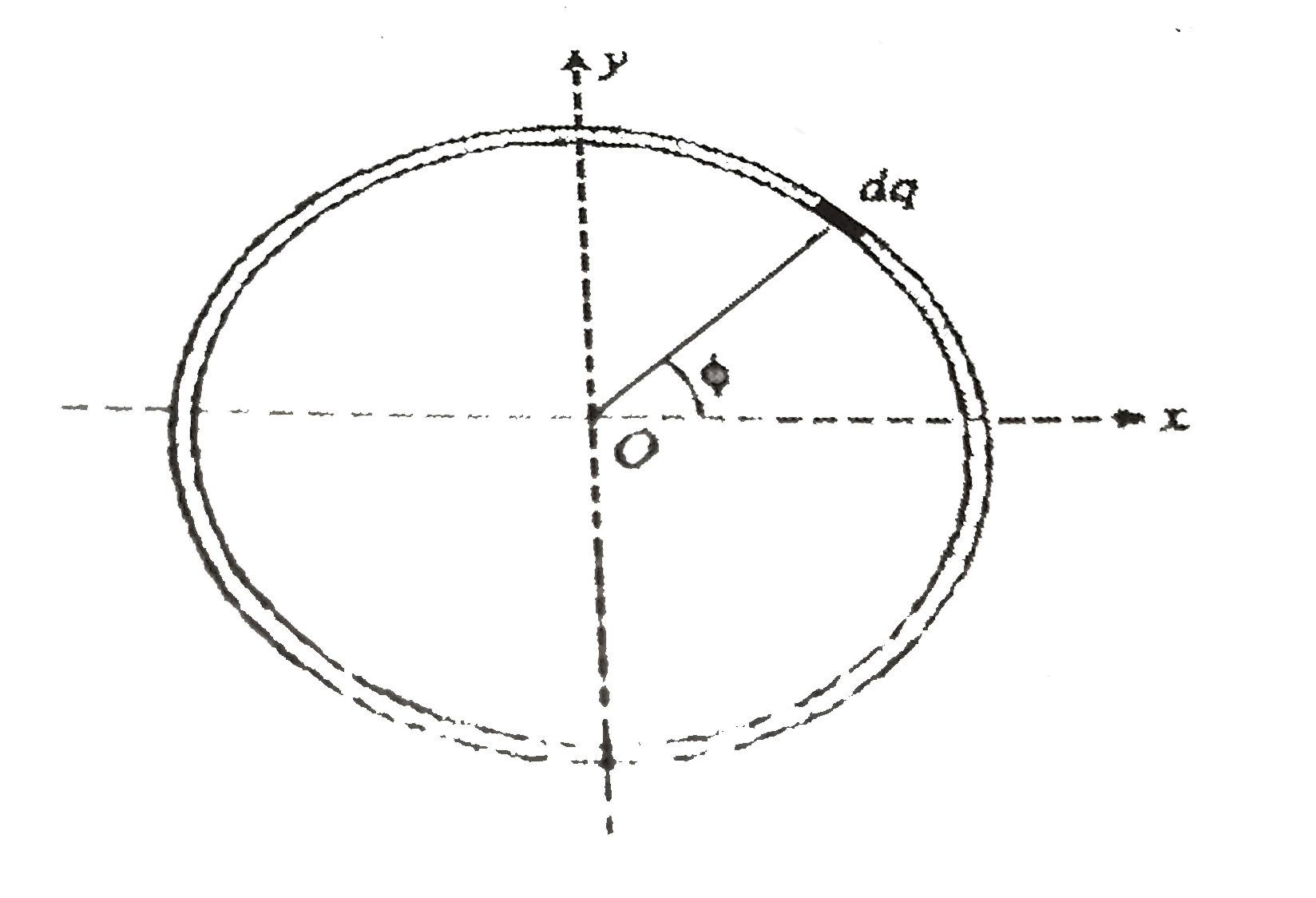
View SolutionA thin non-conducting ring or radius a has a linear charge density λ=λ0sinϕ. A uniform electric field E0ˆi+E0ˆj exist in the region . .Net torque acting on ring is given as :
View SolutionA non - conducting disc of radius R is uniformly charged with surface charge density σ. A disc of radius R2 is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be

View Solution