A non - conducting disc of radius R is uniformly charged with surface charge density σ. A disc of radius R2 is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be

πσR2ε0
σR2πε0
σR(π−1)2πε0
σR(π−1)2ε0
The correct Answer is:C
Step by step video & image solution for A non - conducting disc of radius R is uniformly charged with surface charge density sigma. A disc of radius (R )/(2) is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surface of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surface is .

View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
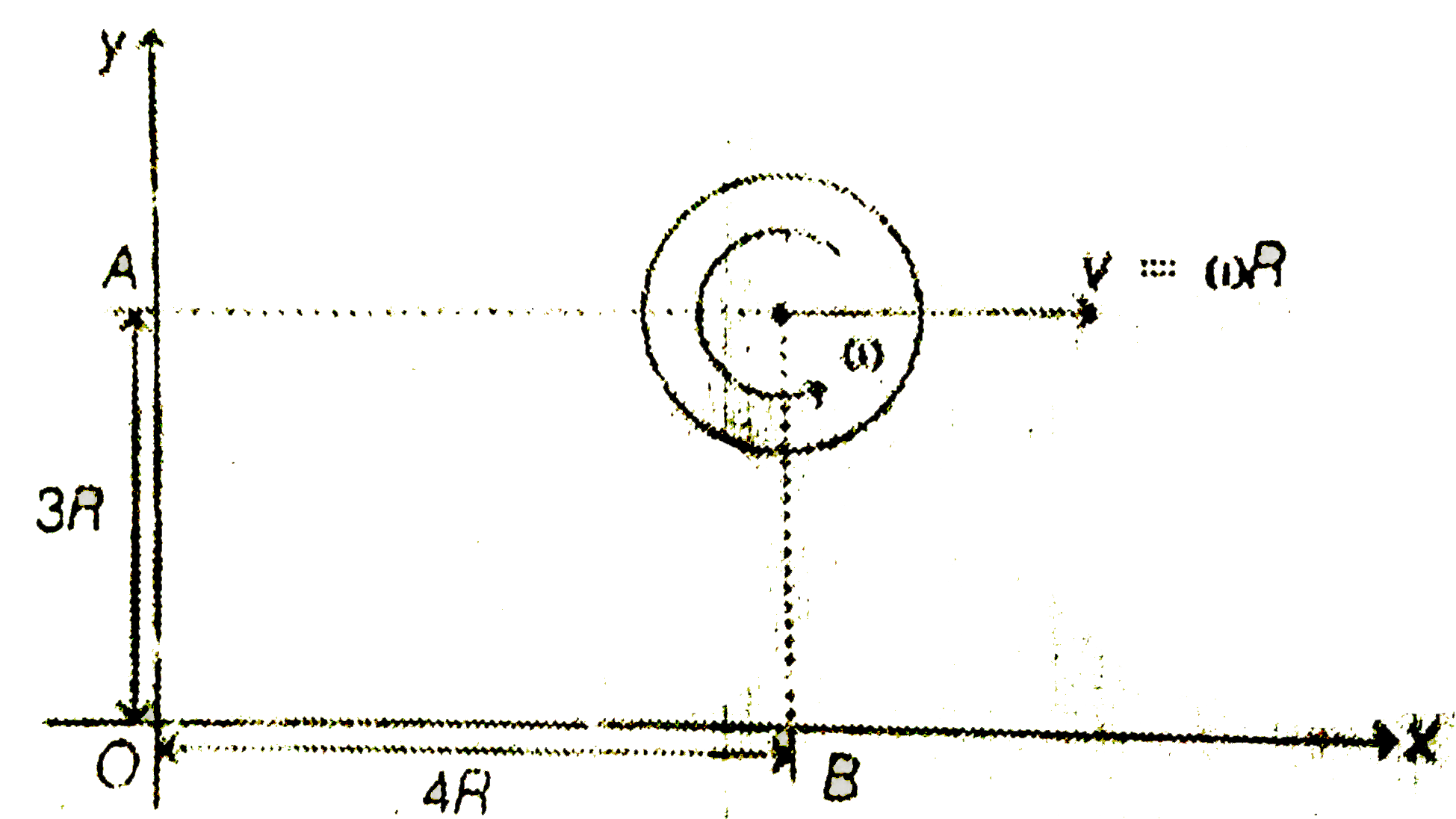
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
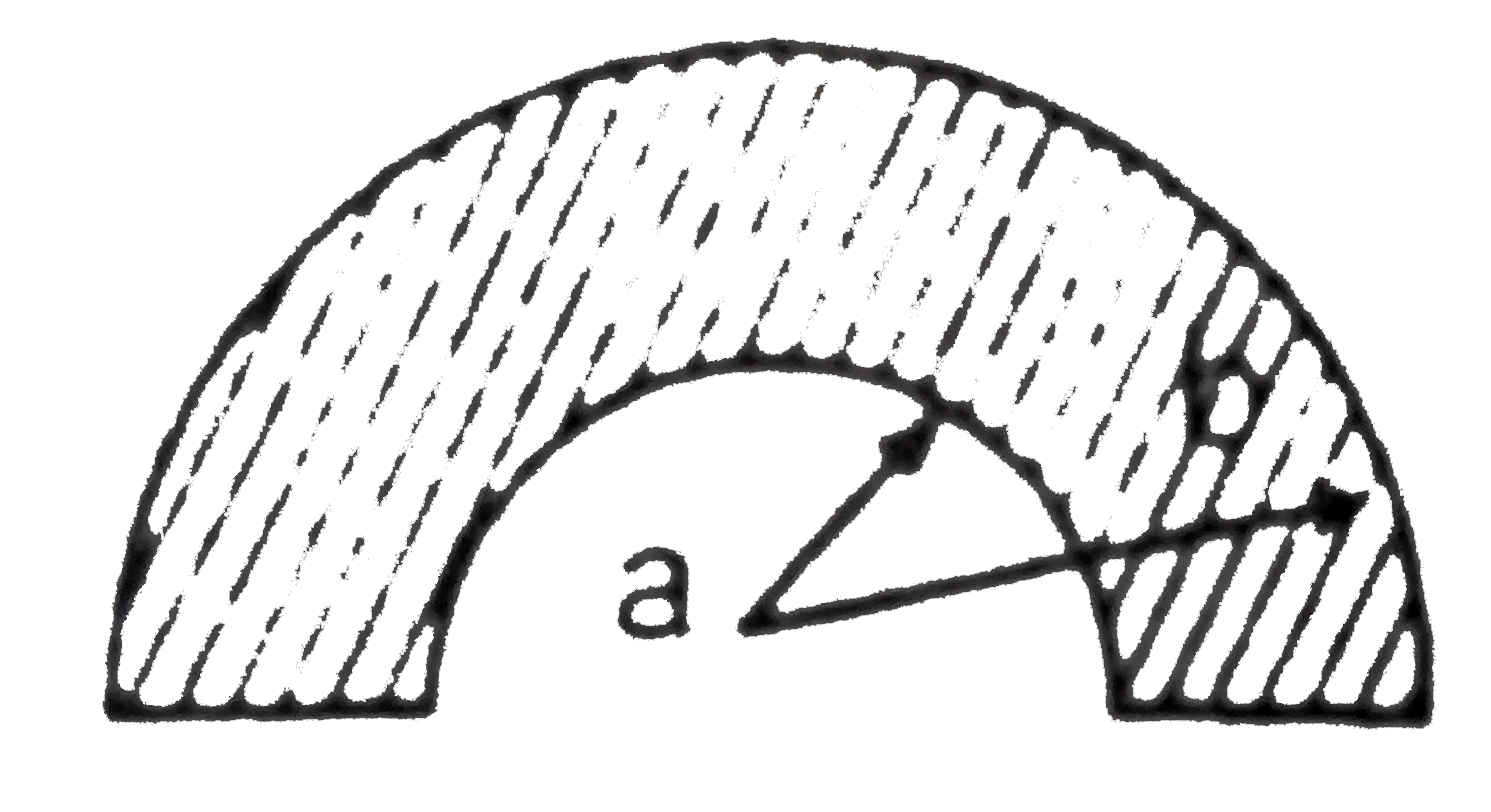
View SolutionA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
View SolutionAn annular disc of inner radius a and outer radius '2a' is uniformly charged with uniform surface charge density σ. Find the potential at a distance 'a' from the centre at a point 'P' lying on the axis.
View SolutionThe distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
View SolutionA flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density σ. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity ω. Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
View Solution
The quarter disc of radius R (see figure) has a uniform surface charge density σ.
(a) Find electric potential at a point (O,O,Z)
(b). Find the Z component of electrif field at (O,O,Z)
View Solution
