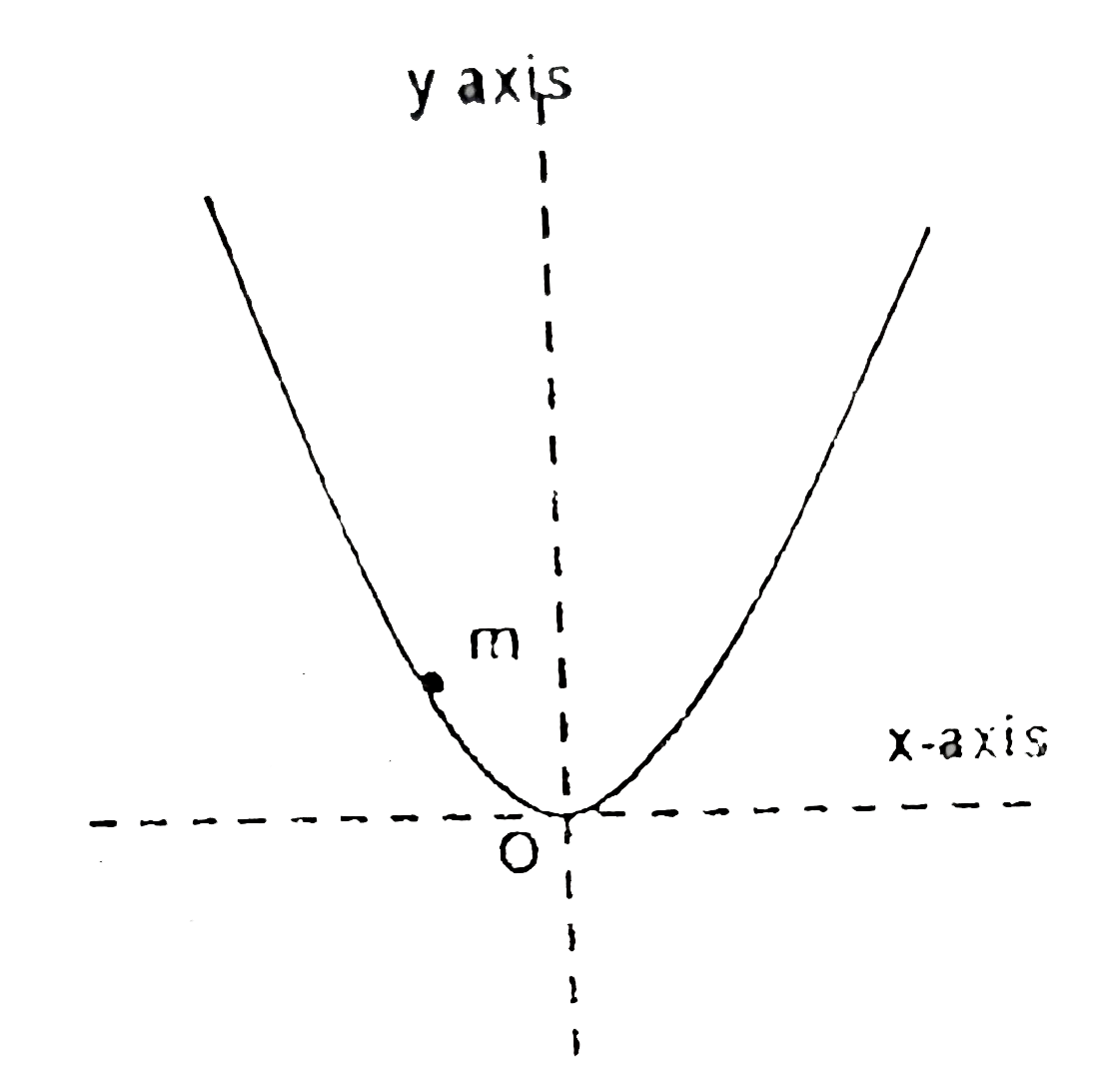
A point mass $m$ is displaced slightly from point $O$ and released. It is constrained to move along parabolic path having equation $x^{2} = k y$ then its angular frequency of oscillation is :

$\sqrt{\frac{g}{2 k}}$

$\sqrt{\frac{2 g}{k}}$

$\sqrt{\frac{g}{k}}$

$\sqrt{\frac{3 g}{2 k}}$

Video Solution

Text Solution

Verified by Experts

$F = - m g sin θ$
$sin θ = tan θ = \frac{d y}{d x} = \frac{2 x}{k}$
$F = - (\frac{2 m g}{k}) x$
$ω = \sqrt{\frac{2 g}{k}}$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

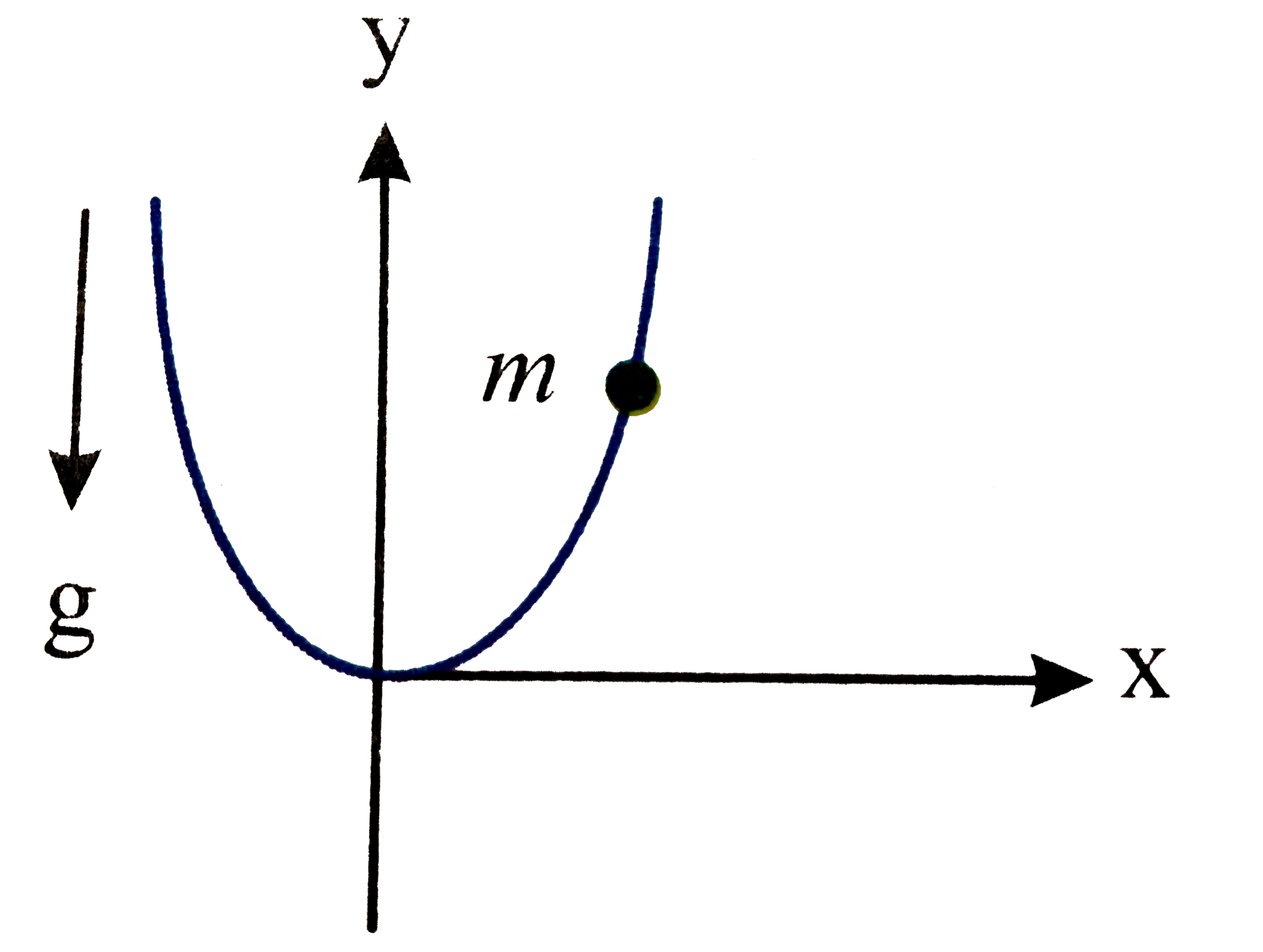
A particle of mass $m$ is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton $x^{2} = 4 a y$ . The angular frequency of small oscillation is given by

View Solution
The equation of a damped simple harmonic motion is $m \frac{d^{2} x}{{d t}^{2}} + b \frac{d x}{d t} + k x = 0$ . Then the angular frequency of oscillation is
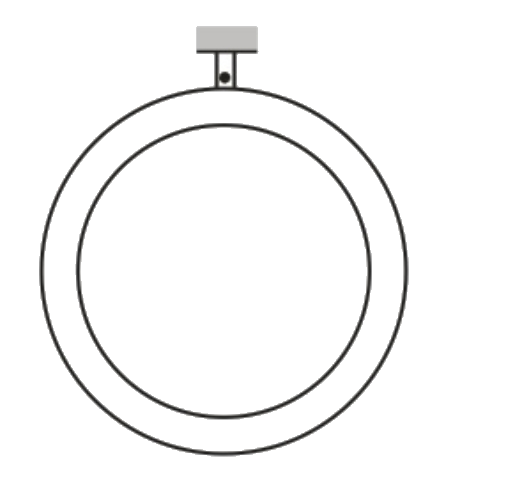
View Solution
A ring of the radius r is suspended from a point on its circumference. If the ring is made to oscillate in the plane of the figure, then the angular frequency of these small oscillations is

View Solution
A small point mass m has a charge q, which is constrained to move inside a narrow frictionless cylinder, At the bae of the cylinder is point mass of charge Q having the same sign as q. If the mass m is displaced by a small amount from its equilibrium position and released. it will exhibit simple harmonic motion. Find the angular frequency of the mass?

View Solution
A ring of radius $r$ is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

View Solution
A ring of radius $r$ is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

View Solution
A block of mass $m$ connected with a smooth prismatic wedge of mass $M$ is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

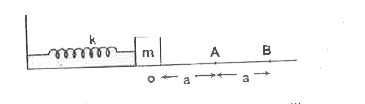
View Solution
In the shown figure, mass m rests on smooth horizontal surface, connected with an ideal spring. If mass is displaced to the point A and released from rest, it reaches the point O in time $t_{0}$ .
Now the block is displaced to the point B and released from rest. How much time it will take in travelling from point A to point O.

View Solution
A non conducting ring of radius R has uniformly distributed positive chargeq. A small particle of mass m and charge $- q$ is placed on the axis of the ring at point P and released If $R > > x$ . The particle will undergo oscillations along the axis of symmerty with an angular frequency that is equal to

View Solution
A particle is moving along a straight line with increasing speed. Its angular momentum about a fixed point on this line :
View Solution

A point mass m is displaced slightly from point O and released. It is constrained to move along parabolic path having equation x2=ky then its angular frequency of oscillation is :

F=−mgsinθ sinθ=tanθ=dydx=2xk F=−(2mgk)x ω=√2gk

Similar Questions

Recommended Questions

A point mass $m$ is displaced slightly from point $O$ and released. It is constrained to move along parabolic path having equation $x^{2} = k y$ then its angular frequency of oscillation is :

$F = - m g sin θ$
$sin θ = tan θ = \frac{d y}{d x} = \frac{2 x}{k}$
$F = - (\frac{2 m g}{k}) x$
$ω = \sqrt{\frac{2 g}{k}}$