A particle of mass m is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton x2=4ay. The angular frequency of small oscillation is given by
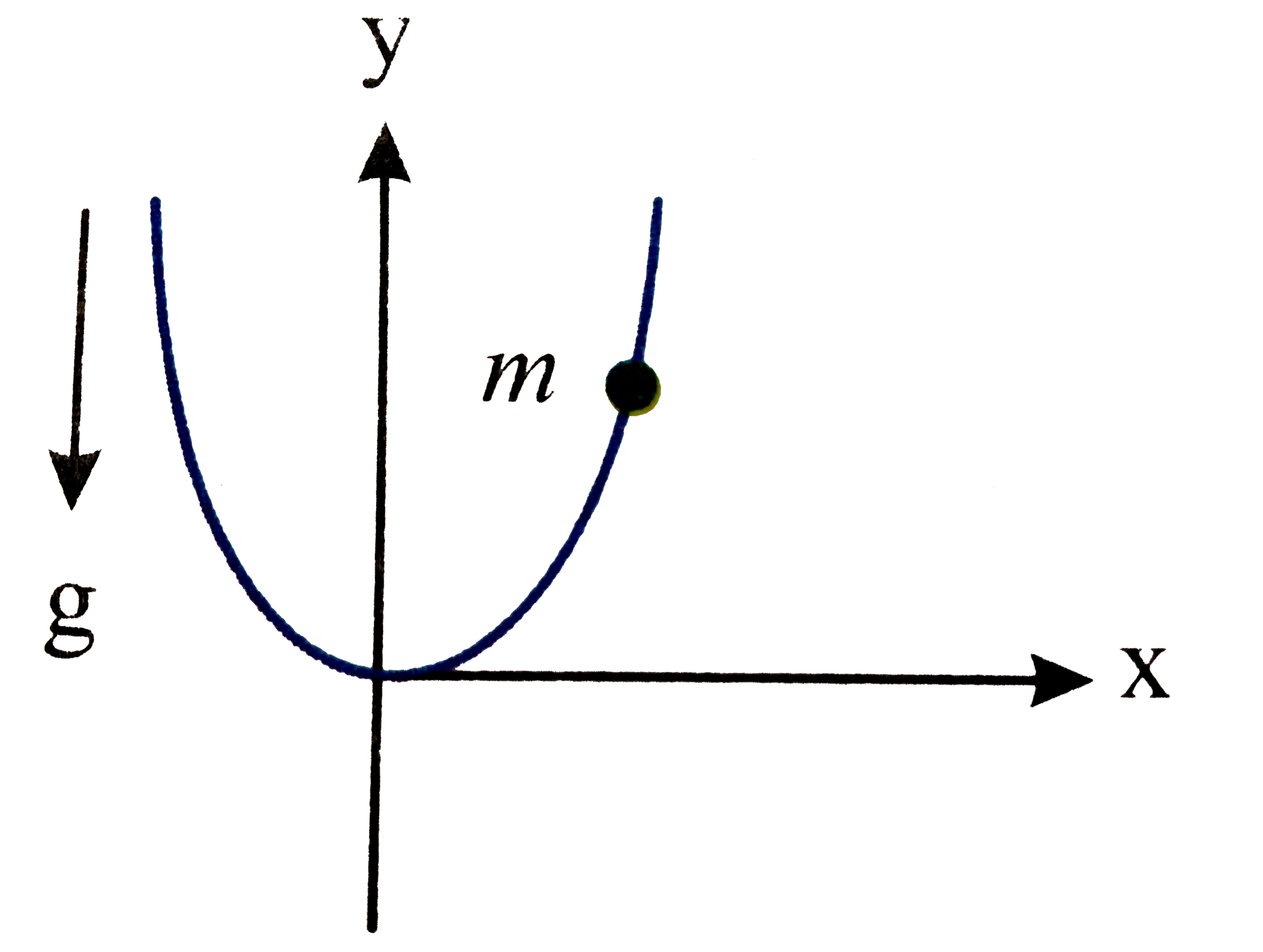
a. √ga
b. √ga
c. √g2a
d. √2ga
The correct Answer is:2
Step by step video & image solution for A particle of mass m is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton x^(2) =4ay. The angular frequency of small oscillation is given by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - EXAMPLE
21 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercise
18 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
7 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
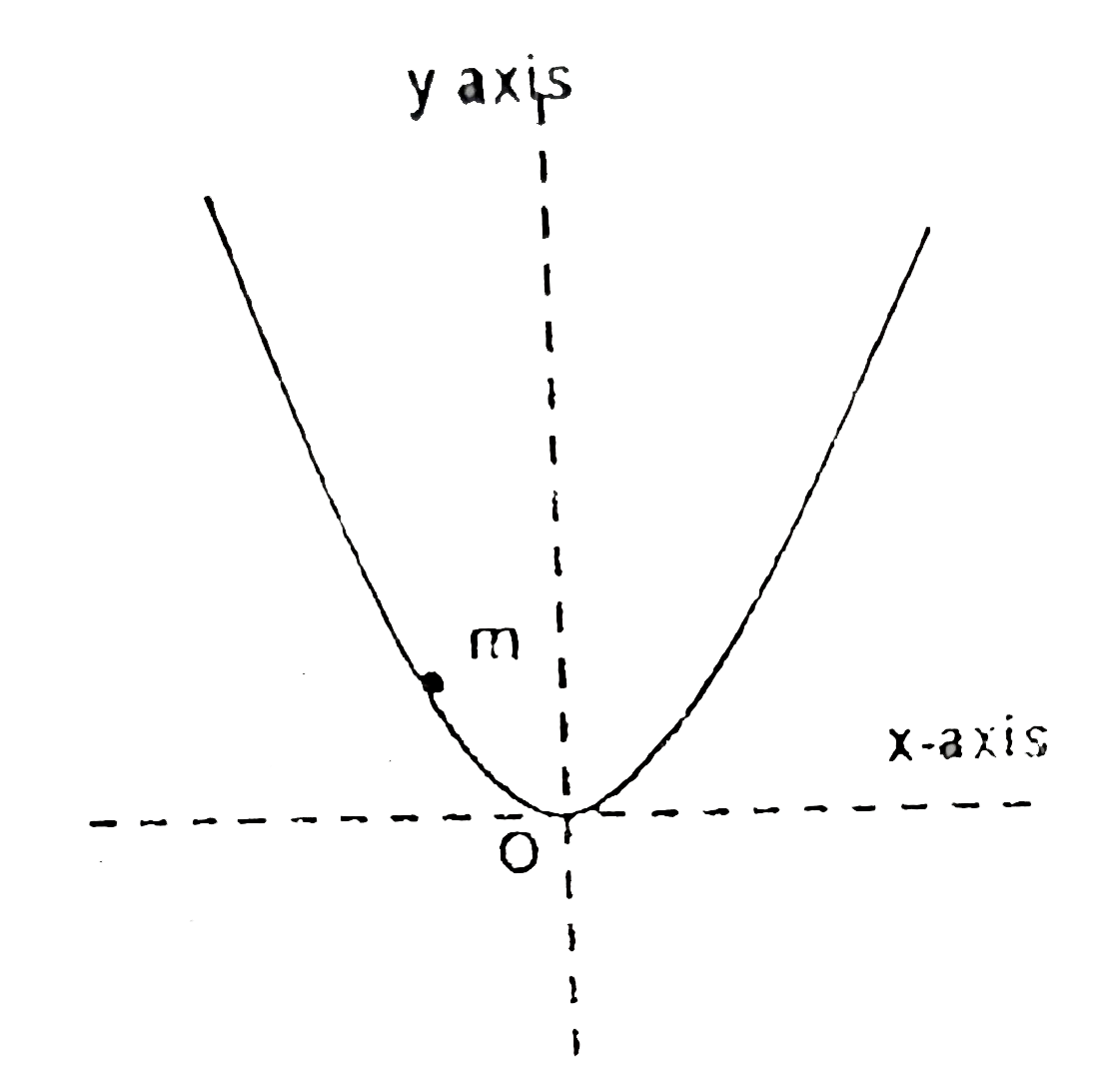
A point mass m is displaced slightly from point O and released. It is constrained to move along parabolic path having equation x2=ky then its angular frequency of oscillation is :
View SolutionA simple harmonic motion is represented by x(t)=sin2ωt−2cos2ωt. The angular frequency of oscillation is given by
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=−ax2+bx4, where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionThe equation of a damped simple harmonic motion is md2xdt2+bdxdt+kx=0. Then the angular frequency of oscillation is
View SolutionA particle executing SHM has a maximum speed of 0.5ms−1 and maximum acceleration of 1.0ms−2. The angular frequency of oscillation is
View SolutionFrom the given figure find the frequency of oscillation of the mass m

View SolutionA block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

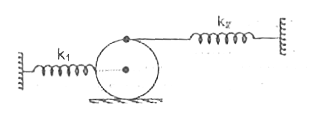
View SolutionA disk of mass m is connected to two springs of stiffness k1andk2 as shown in the figure. Find the angular frequency of the system for small oscillation. Disc can roll on the surface without slipping
View SolutionA particle is attached to a vertical spring and is pulled down a distance 4cm below its equilibrium and is released from rest. The initial upward acceleration is 0.5ms−2. The angular frequency of oscillation is
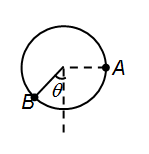
View SolutionA disc of mass M = 4 kg, radius R = 1 m is attached with two blocks A and B of masses 1 kg and 2 kg respectively on rim and is resting on a horizontal surface as shown in the figure. Find angular frequency of small oscillation of arrangement:
View Solution
