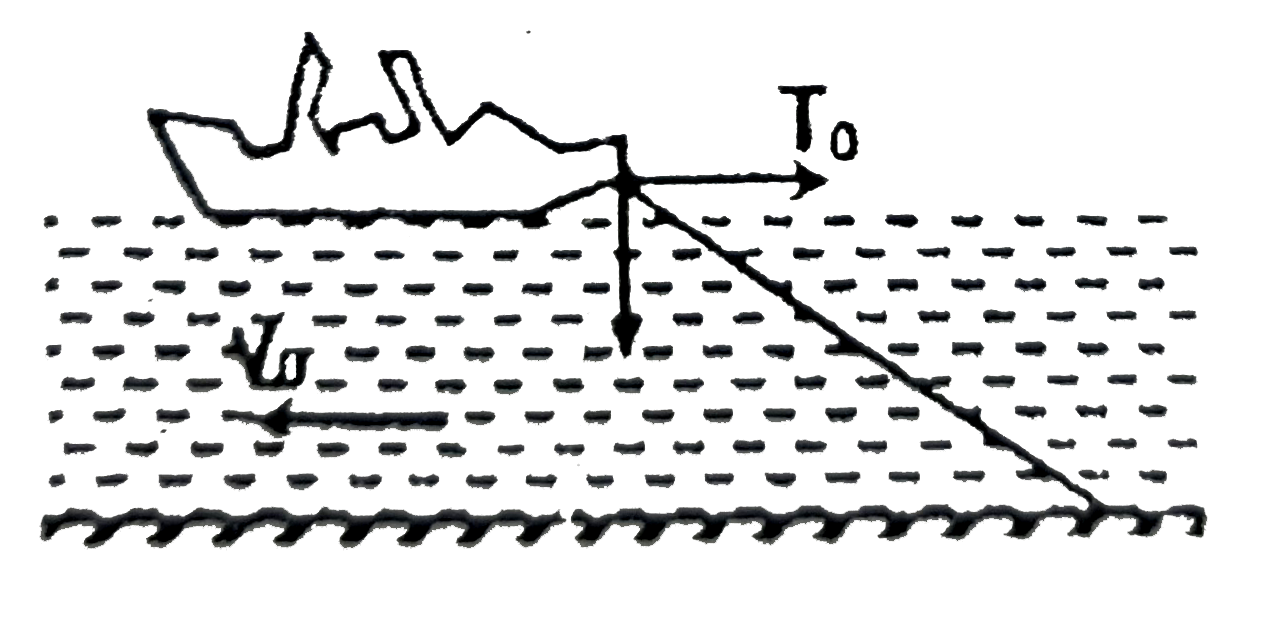
A ship of total mass m is anchored in the middle of a river and water is flowing with a constant velocity v0. The horizontal component of the force exerted on the ship by the anchor chain is T0. If the anchor chain suddenly breaks, determine the time required for the ship to attain a velocity equal to 0.5v0. Assume that the fricitional resistance of the water is proportional to the velocity of the ship relative to the water.
mv0T0ln2
mv02T0ln2
3mv02T0ln2
None of these
Step by step video & image solution for A ship of total mass m is anchored in the middle of a river and water is flowing with a constant velocity v_(0). The horizontal component of the force exerted on the ship by the anchor chain is T_(0). If the anchor chain suddenly breaks, determine the time required for the ship to attain a velocity equal to 0.5 v_(0). Assume that the fricitional resistance of the water is proportional to the velocity of the ship relative to the water. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A ship of mass 3×107 kg initially at rest is pulled by a force of 5×104N through a distance of 3 m. Assume that the resistance due to water is nigligible, the speed of the ship is
A1.5 m/sB60 m/sC0.1 m/sD5 m/s
A motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. How long the motor boat with the shut down engine.
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
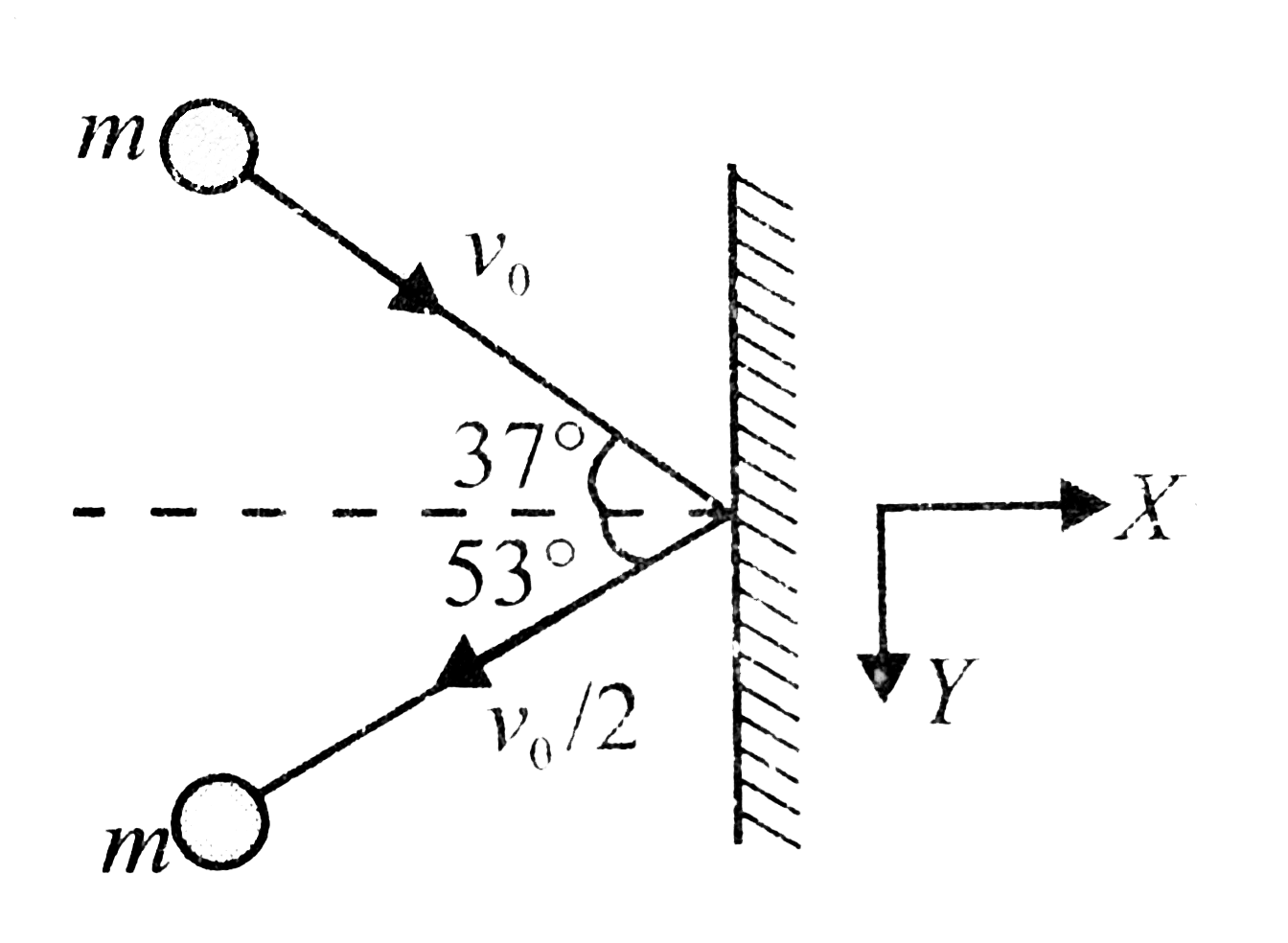
View SolutionA man is rowing a boat with a constant velocity v0 in a river. The contact area of boat is 'A' and coefficient of viscosity is η. The depth of river is 'D' . Find the force required to row the boat.
View SolutionA particle of mass m, moving in a circle of radius R, has a velocity v=v0(1−e−γt) The power delivered to tha particle by the force at t=0 is
View SolutionA ship of mass 3×107kg initially at rest, is pulled by a force of 5×105N through a distance of 3m. Assuming that the resistance due to water is negligible, the speed of the ship is
View SolutionThe angle of depression of a ship from the top a tower of height 50 m is 30∘. Find the horizontal distance between the ship and the tower.
View SolutionThe angle of depression of a ship from the top a tower of height 50 m is 30∘. Find the horizontal distance between the ship and tower.
View Solution

