A motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. How long the motor boat with the shut down engine.
2rv0
rv0
r2v0
∞
To solve the problem, we need to analyze the motion of the motorboat after the engine is shut down. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Forces Acting on the Boat
When the engine is shut down, the only force acting on the motorboat is the resistance of the water, which is given by the equation:
→F=−r→v
where r is a constant of proportionality and →v is the velocity of the boat.
Step 2: Apply Newton's Second Law
According to Newton's second law, the force can also be expressed as:
F=mdvdt
Setting the two expressions for force equal gives:
mdvdt=−rv
Step 3: Rearrange the Equation
Rearranging the equation allows us to separate the variables:
dvv=−rmdt
Step 4: Integrate Both Sides
Now, we will integrate both sides. The left side will be integrated from the initial velocity V0 to 0, and the right side will be integrated from 0 to T:
∫0V0dvv=−rm∫T0dt
This results in:
(lnv)0V0=−rm(t)T0
This simplifies to:
ln(0)−ln(V0)=−rmT
Step 5: Solve for the Constant
Since ln(0) approaches negative infinity, we can express the equation as:
−ln(V0)=−rmT
This implies:
ln(vV0)=−rmT
Step 6: Exponentiate to Solve for Velocity
Exponentiating both sides gives:
v=V0e−rmT
Step 7: Determine Time When Velocity Reaches Zero
As T approaches infinity, the term e−rmT approaches zero. Therefore, the velocity v will reach zero when:
T→∞
Conclusion
Thus, the motorboat will take an infinite amount of time to come to a complete stop after the engine is shut down.
Final Answer
The time taken for the motorboat to come to rest is T=∞.
---
When the engine is shut down, the only force acting on the motorboat is the resistance of the water, which is given by the equation:
→F=−r→v
where r is a constant of proportionality and →v is the velocity of the boat.
According to Newton's second law, the force can also be expressed as:
F=mdvdt
Setting the two expressions for force equal gives:
mdvdt=−rv
Rearranging the equation allows us to separate the variables:
dvv=−rmdt
Now, we will integrate both sides. The left side will be integrated from the initial velocity V0 to 0, and the right side will be integrated from 0 to T:
∫0V0dvv=−rm∫T0dt
This results in:
(lnv)0V0=−rm(t)T0
This simplifies to:
ln(0)−ln(V0)=−rmT
Since ln(0) approaches negative infinity, we can express the equation as:
−ln(V0)=−rmT
This implies:
ln(vV0)=−rmT
Exponentiating both sides gives:
v=V0e−rmT
As T approaches infinity, the term e−rmT approaches zero. Therefore, the velocity v will reach zero when:
T→∞
Thus, the motorboat will take an infinite amount of time to come to a complete stop after the engine is shut down.
The time taken for the motorboat to come to rest is T=∞.
Similar Questions
A motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. The velocity (v) of the motor boat as a function of the distance (s) covered with the shutdown engine is
View SolutionA motor boat of mass m moves along a lake with velocity v0. At t = 0, the engine of the boat is shut down. Resistance offered to the boat is equal to σv2. Then distance covered by the boat when its velocity becomes v0/2 is
View SolutionA motor boat of mass m moves along a lake with velocity V0. At t=0, the engine of the boat is shut down. Magnitude of resistance force offered to the boat is equal to rV. (V is instantaneous speed). What is the total distance covered till it stops completely? [Hint: F(x)=mVdVdx=−rV]
View SolutionA body of mass m is thrown straight up with velocity v0(v0<<ve) Find the velocity v with which the body comes down if the air drag equals kv2, where k is a positive constant and v is the velocity of the body.
View SolutionA boat takes 4 hr upstream and 2 hr down the stream for covering the same distance. The ratio of velocity of boat to the water in river is
View SolutionA ship of total mass m is anchored in the middle of a river and water is flowing with a constant velocity v0. The horizontal component of the force exerted on the ship by the anchor chain is T0. If the anchor chain suddenly breaks, determine the time required for the ship to attain a velocity equal to 0.5v0. Assume that the fricitional resistance of the water is proportional to the velocity of the ship relative to the water.
View SolutionA body of mass m = 4 kg starts moving with velocity v0 in a straight line is such a way that on the body work is being done at the rate which is proportional to the square of velocity as given by P=βv2 where β=0.6932. Find the time elapsed in seconds before velocity of body is doubled.
View SolutionThe force of resistance encountered by water on a motor boat of mass m going in still water with velocity v is proportional to the velocity v. At t=0 when its velocity is v0, then engine shuts off. Find an expression for the position of motor boat at time t and also the distance travelled by the boat before it comes to rest. Take the proportionality constant as k>0.
View SolutionA particle of mass m is moving with constant velocity v0 along the line y=b. At time t=0 it was at the point (0,b). At time t=bv0, the

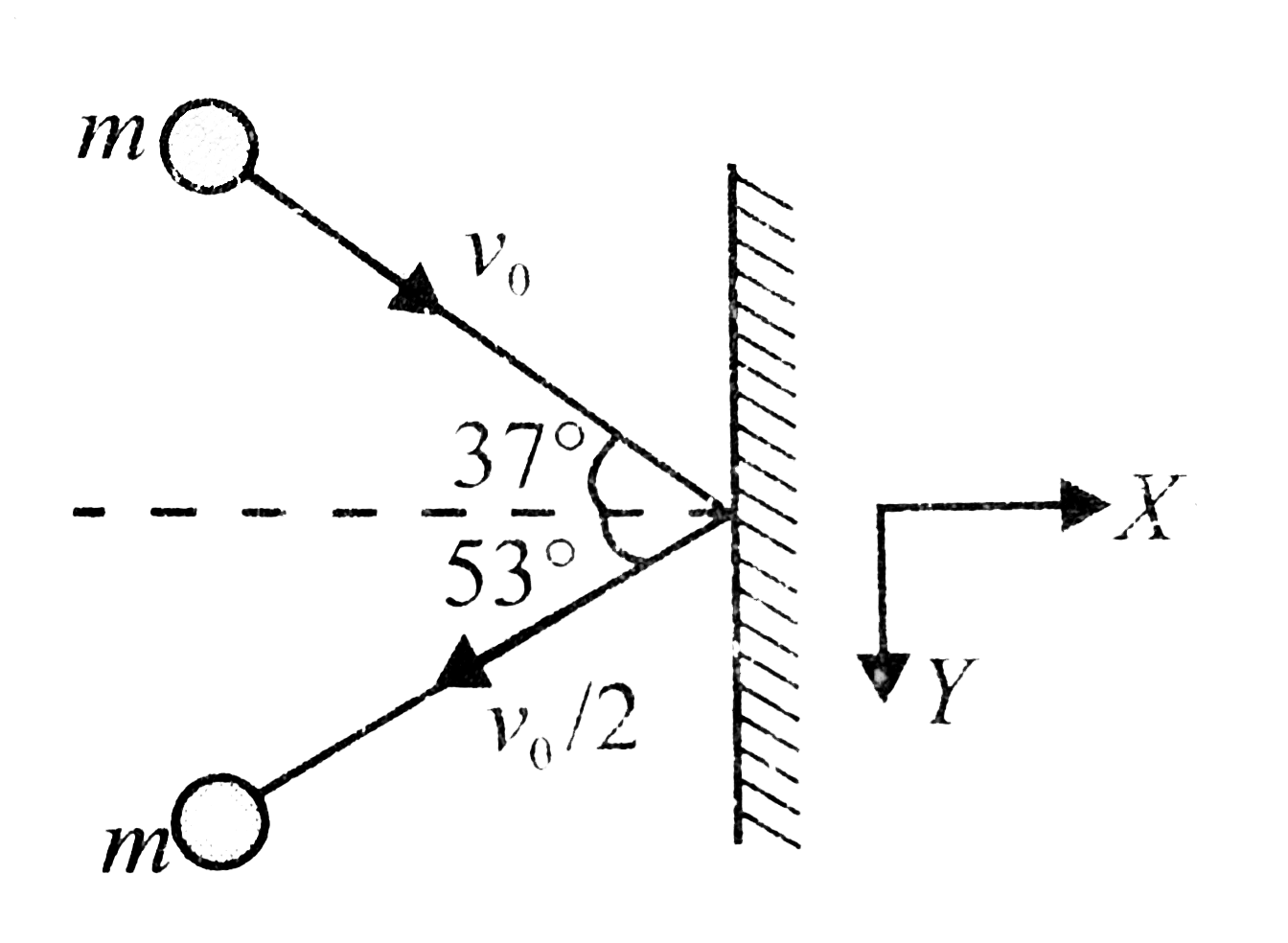
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
View Solution
