Ten litres of a liquid of specific gravity 1.3 is mixed with 6 litres of a liquid of specific gravity 0.8 the specific gravity of mixture is
2.21
1.11
1.15
none of these
To find the specific gravity of the mixture of two liquids, we can follow these steps:
Step 1: Understand the Concept of Specific Gravity
Specific gravity (SG) is defined as the ratio of the density of a substance to the density of water. The density of water is typically taken as 1kg/L.
Step 2: Calculate the Density of Each Liquid
1. Liquid A:
- Specific gravity of liquid A = 1.3
- Density of liquid A (ρA) = Specific gravity × Density of water = 1.3×1kg/L=1.3kg/L
2. Liquid B:
- Specific gravity of liquid B = 0.8
- Density of liquid B (ρB) = Specific gravity × Density of water = 0.8×1kg/L=0.8kg/L
Step 3: Calculate the Mass of Each Liquid
1. Mass of Liquid A:
- Volume of liquid A (VA) = 10 liters
- Mass of liquid A (mA) = Density × Volume = ρA×VA=1.3kg/L×10L=13kg
2. Mass of Liquid B:
- Volume of liquid B (VB) = 6 liters
- Mass of liquid B (mB) = Density × Volume = ρB×VB=0.8kg/L×6L=4.8kg
Step 4: Calculate the Total Mass and Total Volume of the Mixture
1. Total Mass (M):
M=mA+mB=13kg+4.8kg=17.8kg
2. Total Volume (V):
V=VA+VB=10L+6L=16L
Step 5: Calculate the Density of the Mixture
Density of the mixture (ρmix) is given by:
ρmix=MV=17.8kg16L=1.1125kg/L
Step 6: Calculate the Specific Gravity of the Mixture
Specific gravity of the mixture is:
SGmix=ρmixDensity of water=1.1125kg/L1kg/L=1.1125
Final Answer
The specific gravity of the mixture is approximately 1.11.
---
Specific gravity (SG) is defined as the ratio of the density of a substance to the density of water. The density of water is typically taken as 1kg/L.
1. Liquid A:
- Specific gravity of liquid A = 1.3
- Density of liquid A (ρA) = Specific gravity × Density of water = 1.3×1kg/L=1.3kg/L
- Specific gravity of liquid B = 0.8
- Density of liquid B (ρB) = Specific gravity × Density of water = 0.8×1kg/L=0.8kg/L
1. Mass of Liquid A:
- Volume of liquid A (VA) = 10 liters
- Mass of liquid A (mA) = Density × Volume = ρA×VA=1.3kg/L×10L=13kg
- Volume of liquid B (VB) = 6 liters
- Mass of liquid B (mB) = Density × Volume = ρB×VB=0.8kg/L×6L=4.8kg
1. Total Mass (M):
M=mA+mB=13kg+4.8kg=17.8kg
V=VA+VB=10L+6L=16L
Density of the mixture (ρmix) is given by:
ρmix=MV=17.8kg16L=1.1125kg/L
Specific gravity of the mixture is:
SGmix=ρmixDensity of water=1.1125kg/L1kg/L=1.1125
The specific gravity of the mixture is approximately 1.11.
Similar Questions
The specific gravity of ammonia is ………………… .
View Solutionwood with specific gravity of less than 0.2 is
View SolutionWhen equal volumes of two substance are mixed, the specific gravity of the mixurie is 4. When equal weights of the same substance are mixed, the specific gravity of the mixture is 3. The soecufuc gravities of the two substance could be
View Solution40% (w/v) of NaCl solution (specific gravity = 1.12) is equivalent to
View SolutionA cylindrical vessel of diameter 0.3m and height 0.6m is filled two thirds with a liquid of specific gravity 0.8. The vessel is rotated about its axis. a. Determine the speed of rotation when the liquid just starts spilling. b.Find the speed of rotation when the base is just visible. c. What is the percentate of liquid left in the vessel?
View SolutionWhen two substances of specific gravities d1 and d2 are mixed in equal volumes the specific garvity of mixture is found to be ρ1. When they are mixed in equal masses, the specific gravity of the mixture is found to be ρ2.(d1≠d2)
View SolutionA U-tube of uniform cross section (see figure) is partially filled with a liquid I. Another liquid II which does not mix with liquid I is poured into one side. It is found that the liquid levels of the two sides of the tube are the same, while the level of liquid I has risen by 2cm. If the specific gravity of liquid I is 1.1, the specific gravity of liquid II must be
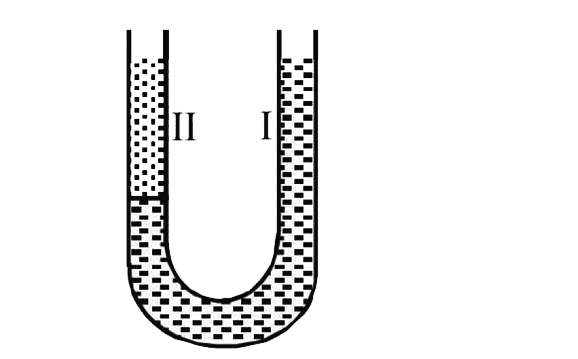 View Solution
View SolutionA solution of acid having 62% by mass of acid has specific gravity of 1.8 g. If the solution is to be diluted to attain a specific gravity of 1.2 then what volume of water should be added to 100 ml of this solution?
View Solutionwood with specific gravity of less than 0.05 occurs in
View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids [The specific gravity of the upper liquid is γ/2 and that of the lower liquid is 2γ, where γ is th especific gracity of the solid ball.] The fraction of the volume of the ball that will be in upper liquid is
View Solution

