A solid uniform ball of volume V floats on the interface of two immiscible liquids [The specific gravity of the upper liquid is γ/2 and that of the lower liquid is 2γ, where γ is th especific gracity of the solid ball.] The fraction of the volume of the ball that will be in upper liquid is
23V
13V
V4
3V4
The correct Answer is:A
To solve the problem of determining the fraction of the volume of a solid uniform ball that floats on the interface of two immiscible liquids, we can follow these steps:
Step 1: Define Variables
Let:
- V = total volume of the ball
- V′ = volume of the ball submerged in the upper liquid
- V′′ = volume of the ball submerged in the lower liquid
- The specific gravity of the solid ball = γ
- The specific gravity of the upper liquid = γ2
- The specific gravity of the lower liquid = 2γ
Step 2: Relate Volumes
Since the ball is floating, the total volume of the ball can be expressed as:
V=V′+V′′
Step 3: Express Weight of the Ball
The weight of the ball W can be expressed in terms of its specific gravity:
W=Specific Gravity×Volume×g=γVg
Step 4: Calculate Buoyant Forces
The buoyant force from the upper liquid F1 is given by:
F1=Density of upper liquid×V′×g=(γ2)V′g
The buoyant force from the lower liquid F2 is given by:
F2=Density of lower liquid×V′′×g=(2γ)V′′g
Step 5: Set Up the Equation for Equilibrium
For the ball to float, the total buoyant force must equal the weight of the ball:
F1+F2=W
Substituting the expressions we derived:
(γ2)V′g+(2γ)V′′g=γVg
Step 6: Simplify the Equation
Cancelling g from both sides, we have:
γ2V′+2γV′′=γV
Dividing through by γ:
12V′+2V′′=V
Step 7: Substitute V′′
From V=V′+V′′, we can express V′′ as:
V′′=V−V′
Substituting this into the buoyancy equation:
12V′+2(V−V′)=V
Expanding and simplifying:
12V′+2V−2V′=V
2V−32V′=V
Rearranging gives:
2V−V=32V′
V=32V′
Step 8: Solve for V′
Now, solving for V′:
V′=23V
Step 9: Find the Fraction of Volume in Upper Liquid
The fraction of the volume of the ball that is in the upper liquid is:
Fraction=V′V=23VV=23
Final Answer
The fraction of the volume of the ball that will be in the upper liquid is 23.
---
Let:
- V = total volume of the ball
- V′ = volume of the ball submerged in the upper liquid
- V′′ = volume of the ball submerged in the lower liquid
- The specific gravity of the solid ball = γ
- The specific gravity of the upper liquid = γ2
- The specific gravity of the lower liquid = 2γ
Since the ball is floating, the total volume of the ball can be expressed as:
V=V′+V′′
The weight of the ball W can be expressed in terms of its specific gravity:
W=Specific Gravity×Volume×g=γVg
The buoyant force from the upper liquid F1 is given by:
F1=Density of upper liquid×V′×g=(γ2)V′g
F2=Density of lower liquid×V′′×g=(2γ)V′′g
For the ball to float, the total buoyant force must equal the weight of the ball:
F1+F2=W
Substituting the expressions we derived:
(γ2)V′g+(2γ)V′′g=γVg
Cancelling g from both sides, we have:
γ2V′+2γV′′=γV
Dividing through by γ:
12V′+2V′′=V
From V=V′+V′′, we can express V′′ as:
V′′=V−V′
Substituting this into the buoyancy equation:
12V′+2(V−V′)=V
Expanding and simplifying:
12V′+2V−2V′=V
2V−32V′=V
Rearranging gives:
2V−V=32V′
V=32V′
Now, solving for V′:
V′=23V
The fraction of the volume of the ball that is in the upper liquid is:
Fraction=V′V=23VV=23
The fraction of the volume of the ball that will be in the upper liquid is 23.
Similar Questions
A solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the u of upper liquid is

View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the upper liquid is

View SolutionA solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.

View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
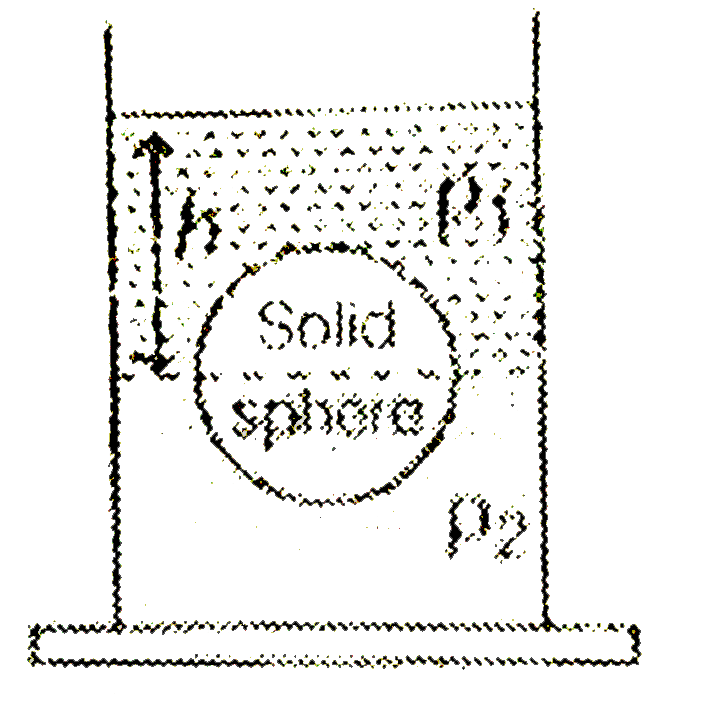
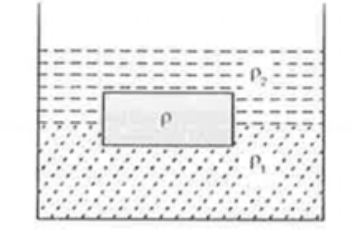
View SolutionA cube of density p is just balanced at interface of two unmixable liquid A and B having density p1 and p2 respectively as shown, then the fraction of volume of cube in the upper liquid is (p2<p<p1)
View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densites ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View SolutionA block of ice is floating in a liquid of specific gravity 1.2 contained in the beaker. What will be the effect on the level of liquid in the beaker when the whole ice melts?
View Solution10 mL of liquid carbon disulphide (specific gravity 2.63) is burnt in oxygen. Find the volume of the resulting gases measured at STP.
View SolutionUniform speed of 2 cm diameter ball is 20cm/s in a viscous liquid. Then, the speed of 1 cm diameter ball in the same liquid is
View SolutionThe speed of a ball of radius 2 cm in a viscous liquid is 20 cm/s. Then the speed of ball of radius I cm in the same liquid is
View Solution