A gun is mounted on a trolley which can move uniformly with speed along the -axis. Two shots are find from the origin with the gun making an angle with the horizontal such that in the first case the trolley is moving along the positive -axis and in the second case moving along the negative - axis. The respective range of the projectile is and , along the axis. Find the velocity of the trolley in . (Assume height of the trolley to be negligible)(given ).
To solve the problem step by step, we will use the principles of projectile motion and the effects of the trolley's movement on the projectile's range.
Step 1: Understand the Problem
We have a gun mounted on a trolley that can move along the x-axis. The gun fires at an angle of 30 degrees to the horizontal. The trolley moves in two different directions, and we need to find its speed based on the ranges of the projectile.
Step 2: Define Variables
- Let v be the speed of the trolley (in m/s).
- Let u be the speed of the projectile (in m/s).
- The angle of projection θ=30∘.
- The range when the trolley moves in the positive x-direction R1=250m.
- The range when the trolley moves in the negative x-direction R2=200m.
- The acceleration due to gravity g=10m/s2.
Step 3: Write the Range Equations
For the first case (trolley moving in the positive x-direction):
R1=(ucos30∘+v)t
250=(u√32+v)t(1)
For the second case (trolley moving in the negative x-direction):
R2=(ucos30∘−v)t
200=(u√32−v)t(2)
Step 4: Find Time of Flight
The time of flight t for a projectile is given by:
t=2usinθg
Substituting θ=30∘:
t=2u⋅1210=u10(3)
Step 5: Substitute t into Range Equations
Substituting equation (3) into equations (1) and (2):
From equation (1):
250=(u√32+v)u10
2500=u√32u+vu10
2500=√32u2+vu10(4)
From equation (2):
200=(u√32−v)u10
2000=u√32u−vu10
2000=√32u2−vu10(5)
Step 6: Solve the Equations
Now, we have two equations (4) and (5):
1. 2500=√32u2+vu10
2. 2000=√32u2−vu10
Adding these two equations:
2500+2000=(√32u2+vu10)+(√32u2−vu10)
4500=√3u2
u2=4500√3(6)
Step 7: Substitute u2 back to find v
Substituting u2 from equation (6) into either equation (4) or (5). Let's use equation (4):
2500=√32(4500√3)+vu10
2500=2250+vu10
250=vu10
vu=2500(7)
Step 8: Substitute u from equation (6) into (7)
From equation (6), u=√4500√3:
v√4500√3=2500
v=2500√3√4500=2500√330√5=250√33√5≈50m/s
Final Answer
The velocity of the trolley v is approximately 5m/s.
We have a gun mounted on a trolley that can move along the x-axis. The gun fires at an angle of 30 degrees to the horizontal. The trolley moves in two different directions, and we need to find its speed based on the ranges of the projectile.
- Let v be the speed of the trolley (in m/s).
- Let u be the speed of the projectile (in m/s).
- The angle of projection θ=30∘.
- The range when the trolley moves in the positive x-direction R1=250m.
- The range when the trolley moves in the negative x-direction R2=200m.
- The acceleration due to gravity g=10m/s2.
For the first case (trolley moving in the positive x-direction):
R1=(ucos30∘+v)t
250=(u√32+v)t(1)
R2=(ucos30∘−v)t
200=(u√32−v)t(2)
The time of flight t for a projectile is given by:
t=2usinθg
Substituting θ=30∘:
t=2u⋅1210=u10(3)
Substituting equation (3) into equations (1) and (2):
250=(u√32+v)u10
2500=u√32u+vu10
2500=√32u2+vu10(4)
200=(u√32−v)u10
2000=u√32u−vu10
2000=√32u2−vu10(5)
Now, we have two equations (4) and (5):
1. 2500=√32u2+vu10
2. 2000=√32u2−vu10
2500+2000=(√32u2+vu10)+(√32u2−vu10)
4500=√3u2
u2=4500√3(6)
Substituting u2 from equation (6) into either equation (4) or (5). Let's use equation (4):
2500=√32(4500√3)+vu10
2500=2250+vu10
250=vu10
vu=2500(7)
From equation (6), u=√4500√3:
v√4500√3=2500
v=2500√3√4500=2500√330√5=250√33√5≈50m/s
The velocity of the trolley v is approximately 5m/s.
Similar Questions
A ball is thrown from the origin in the x-y plane with velocity 28.28 m/s at an angle 45∘ to the x-axis. At the same instant a trolley also starts moving with uniform velocity of 10 m/s along the positive x-axis. Initially rear end of the trolley is located at 38 m from the origin. Determine the time and position at which the ball hits the trolley.
View SolutionA mass m moving horizontally (along the x-axis) with velocity v collides and stricks to a mass of 3 m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is
View SolutionA plank fitted with a gun is moving on a horizontal surface with speed of 4m//s along the positive x-axis. The z-axis is in vertically upward direction. The mass of the plank including the mass of the gun is 50 kg. When the plank reaches the origin, a shell of mass 10 kg is fired at an angle of 60^@ with the positive x-axis with a speed of v = 20m//s with respect to the gun in x-z plane. Find the position vector of the shell at t=2 s after firing it. Take g = 9.8 m//s^2 .
05:31View SolutionA proton is moving along the negative direction of X-axis in a magnetic field directed along the positive direction of Y-axis. The proton will be deflected along the negative direction of
02:17View Solutionसमान द्रव्यमान का एक आदमी व एक तख्ता समान वेग v से धनात्मक x -अक्ष के अनुदिश चल रहे है। उसी समय आदमी धरातल के सापेक्ष v वेग से ऋणात्मक x अक्ष के अनुदिश कूदता है तो तख्ते की चाल होगी।
 02:39View Solution
02:39View SolutionA railway flatcar whose mass together with the artillery gun is M moves at a speed V along the x-axis
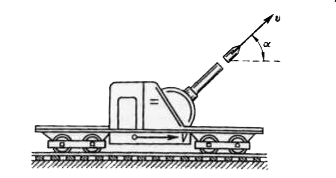
The gun barrel makes an angle a with this axis. A projectile of mass m leaves the gun at speed v (relative to the gun) in the direction of the flatcar's motion. Find the speed of the flatcar after the gun has been fired. What should the speed of the flatcar be for it to stop after the firing? Neglect friction.
Put M = 10 tons, m = 120 kg, V = 6.0 mis, v = 900 m/s, α=30°.View SolutionOn a frictionless horizontal surface , assumed to be the x-y plane , a small trolley A is moving along a straight line parallel to the y- axis ( see figure) with a constant velocity of (sqrt(3)-1) m//s . At a particular instant , when the line OA makes an angle of 45(@) with the x - axis , a ball is thrown along the surface from the origin O . Its velocity makes an angle phi with the x - axis and it hits the trolley . (a) The motion of the ball is observed from the frame of the trolley . Calculate the angle theta made by the velocity vector of the ball with the x- axis in this frame . (b) Find the speed of the ball with respect to the surface , if phi = (4 theta )//(3) .
05:44View Solutionक्षैतिज (x- अक्ष के अनुदिश )v वेग से गति करता हुआ द्रव्यमान m उर्ध्वाधरतः2v वेग से ऊपर की और गति (y अक्ष के अनुदिश ) करते हुए 3m द्रव्यमान से टकराकर उससे जुड़ जाता है संयुक्त द्रव्यमान का अंतिम वेग है
03:14View Solution

