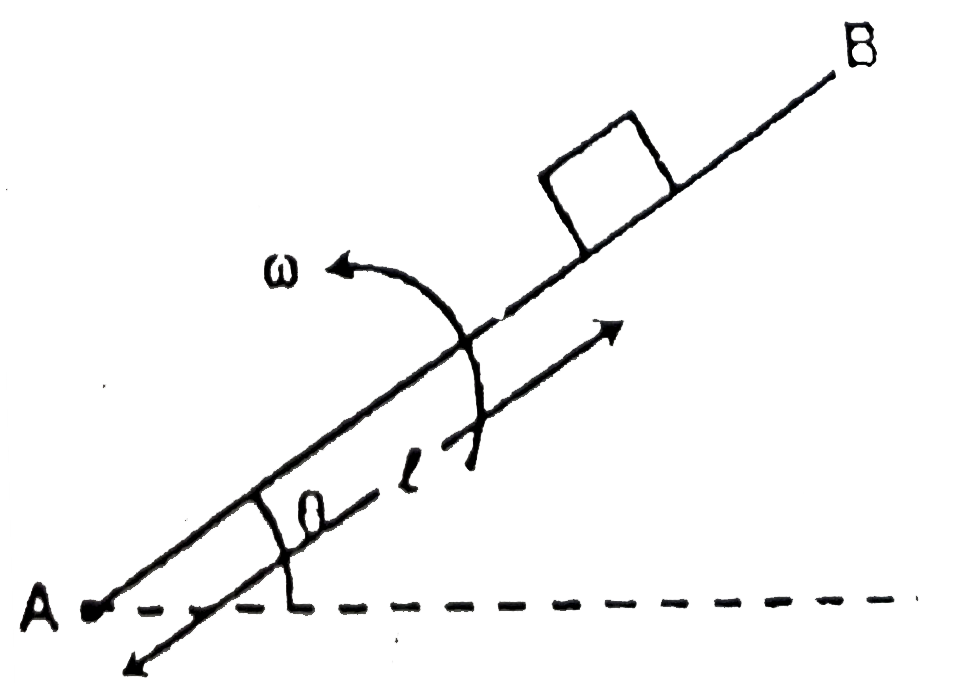
A plank is rotating in a vertical plane about one of its ends with a constant angular velocity ω=√2rad/s. A block of mass m=2kg is placed at a distance l=1m from its end A (see figure) which is hinged. The block starts sliding down when the plank makes an angle θ=30∘ with the horizontal. If coefficient of friction between the plank and the block is μ and given that μ2=k/25. Find the value of k.
1v−1u=1f
v−u=x,
1u+x−1u=1f
⇒1u+x=1u+1f
u+x=ufu+f
x=ufu+f−u=u[fu+f−1]
x=−u2u+f
differentiating w.r.t. x,
∴δx=[−2uu+f+u2(u+f)2]δu
=−2u(u+f)+u2(u+f)2δu
=−u2+2uf(u+f)2δu
δx=(u+f)2+f2(u+f)2=[(fu+f)−1]δu
δu=a<<|u|=|3f|
δx=[(f−3f+f)2−1]a=−34a
Amplitude =|δx|=34a
Similar Questions
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
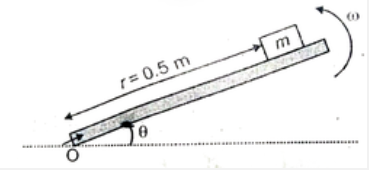
View SolutionA wooden plank OA rotates in vertical plane about horizontal axis through O with a constant angular velocity ω=3rad/s . As it passes the position θ=0 , a small mass m is placed upon it at a radial distance r=0⋅5 m . If the mass m starts sliding at θ=37∘ , find the coefficient of friction between mass and the plane .
 View Solution
View SolutionA block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
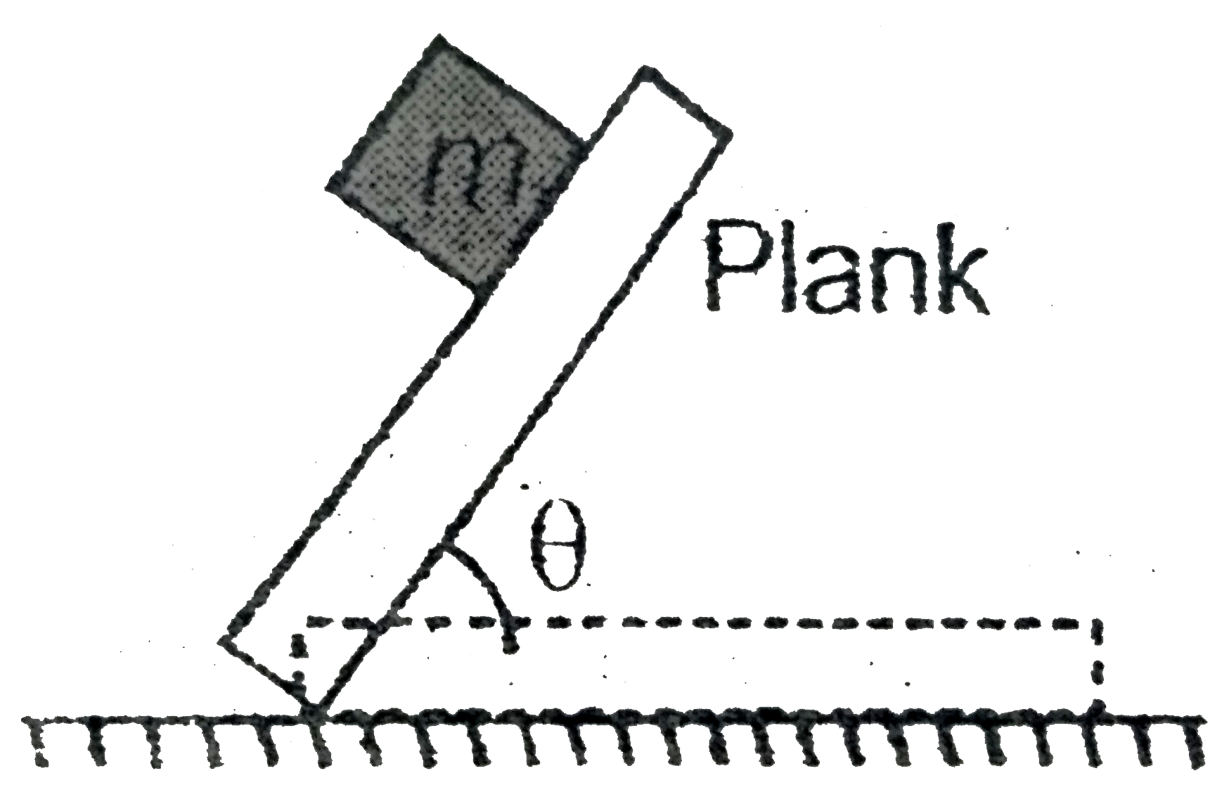
View SolutionA block of mass m is kept on a plank . The coefficient of friction between the plank and block is 1. The plank is slowly raised from one end so that it makes angle θ with horizontal . The forces of friction acting on the plank , when θ=30∘andθ60∘ are respectively,
 View Solution
View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is
 View Solution
View Solution

