A laser beam propagates through a spherically symmetric medium, as shown in the figure. The refractive index varies with the distance to the symmetry centre C by the law μ(r)=μ0rr0, where μ0=1, r0=3cm, r0≤r<∞. The beam's trajectory lies in the plane that includes C. At distance r1=8√2cm the beam makes an angle ϕ=30∘ with →r1 as shown in the figure. Find the minimum distance (in cm) the beam reach relative to the symmetry centre C.

μ1sinϕ=μ2sinθ
r1sinθ'=r2sinθ
sinϕ=r2r1sinθ'
μ1sinϕ=μ2r2r1sinθ'
r1μ1sinϕ=r2μ2sinθ'
r1μ0r1r0sin30∘=μ0r2minr0sin90∘ (At minimum separation)
rmin=r1√sin30∘=8cm

Similar Questions
Variation of μr (relative permeability) with magnetizing field as shown in figure is for

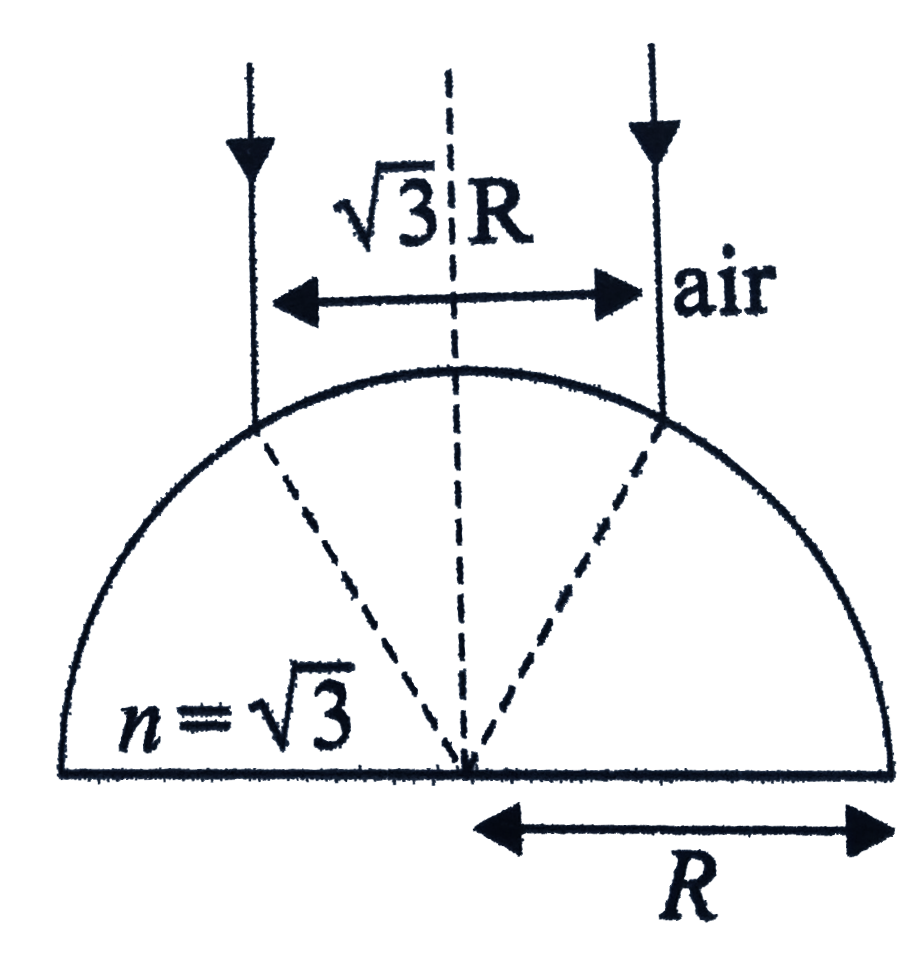
View SolutionA light beam of diameter √3R is incident symmetrically on a glass hemispher of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemispher.
View SolutionThe mass density of a planet of radius R varie with the distance r form its centre as ρ(r)=p0(1−r2R2). Then the graviational field is maximum at :
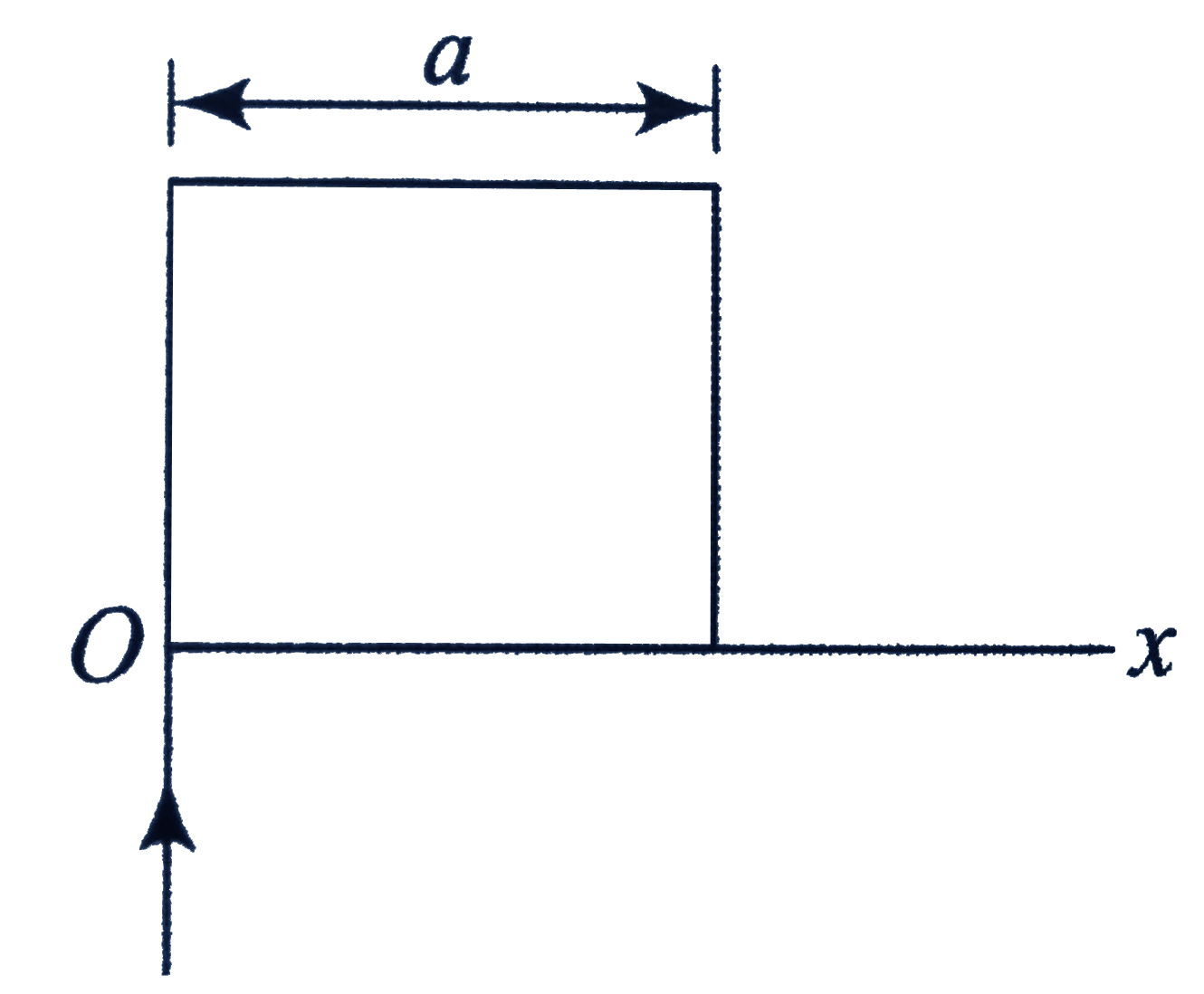
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View SolutionA light beam of diameter √3R is incident symmetrically on a glass hemisphere of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemisphere.

View SolutionLet there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
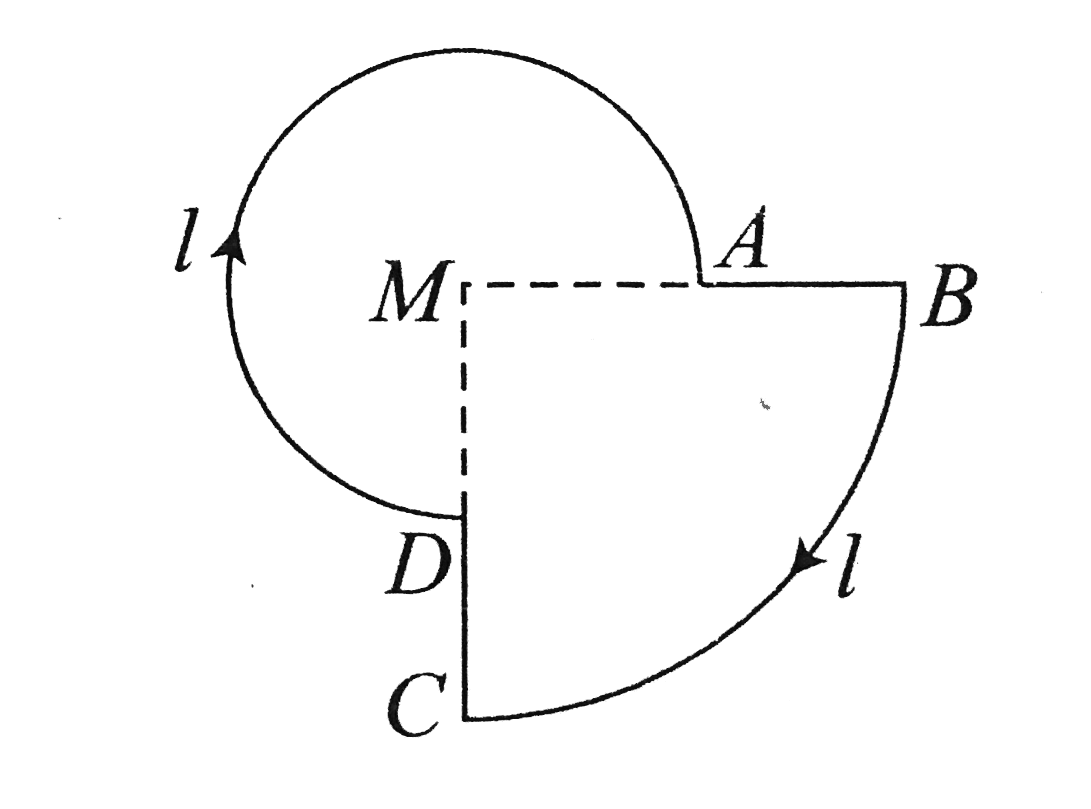
View SolutionA current I is flowing thorugh the loop. The direction of the current and the shpae of the loop are as the shown in the figure. The magnetic fild at the centre of the loop is μ0IR times
(MA=R,MB=2R,∠DMA=90∘)
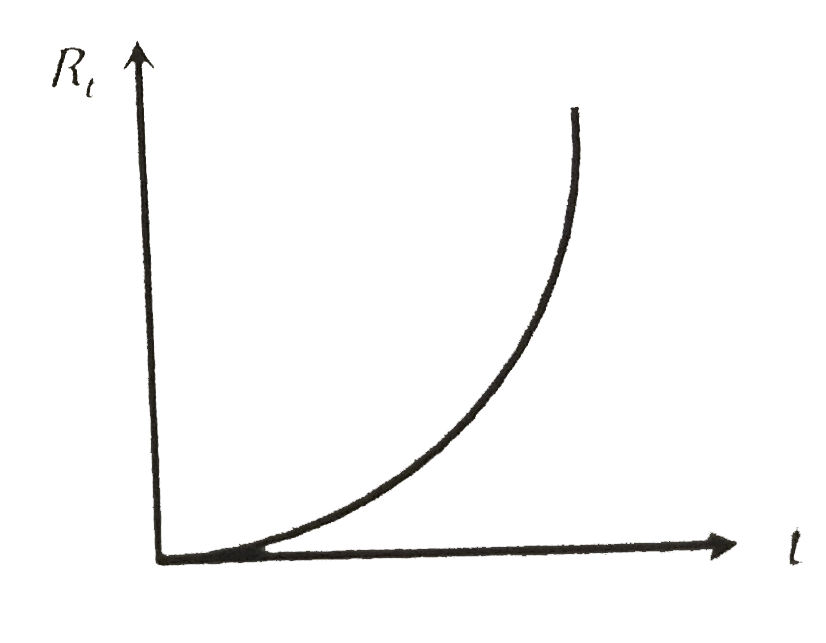
View SolutionThe resistance R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
View SolutionTwo identical plano-convex lenses L1(μ1−1.4) and L2(μ2−1.5)
of radii of curvature R=20cm are placed as shown in Figure.
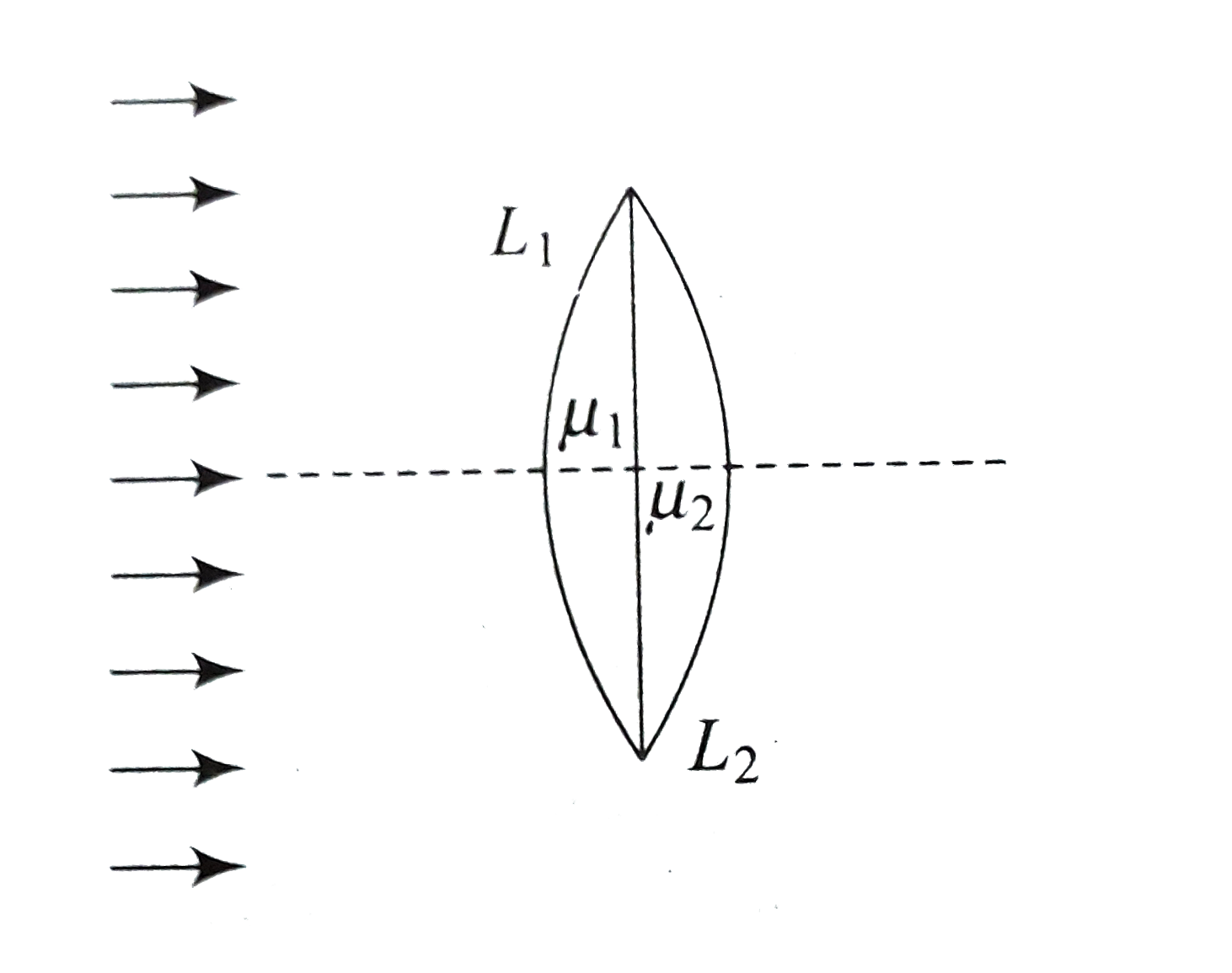
Q. Find the position of the image of the parallel beam of light relative to the common principal axis.
View SolutionIn the curcuit shown in figure R1=R2=R3=10Ω. Find the currents through R1 and R2
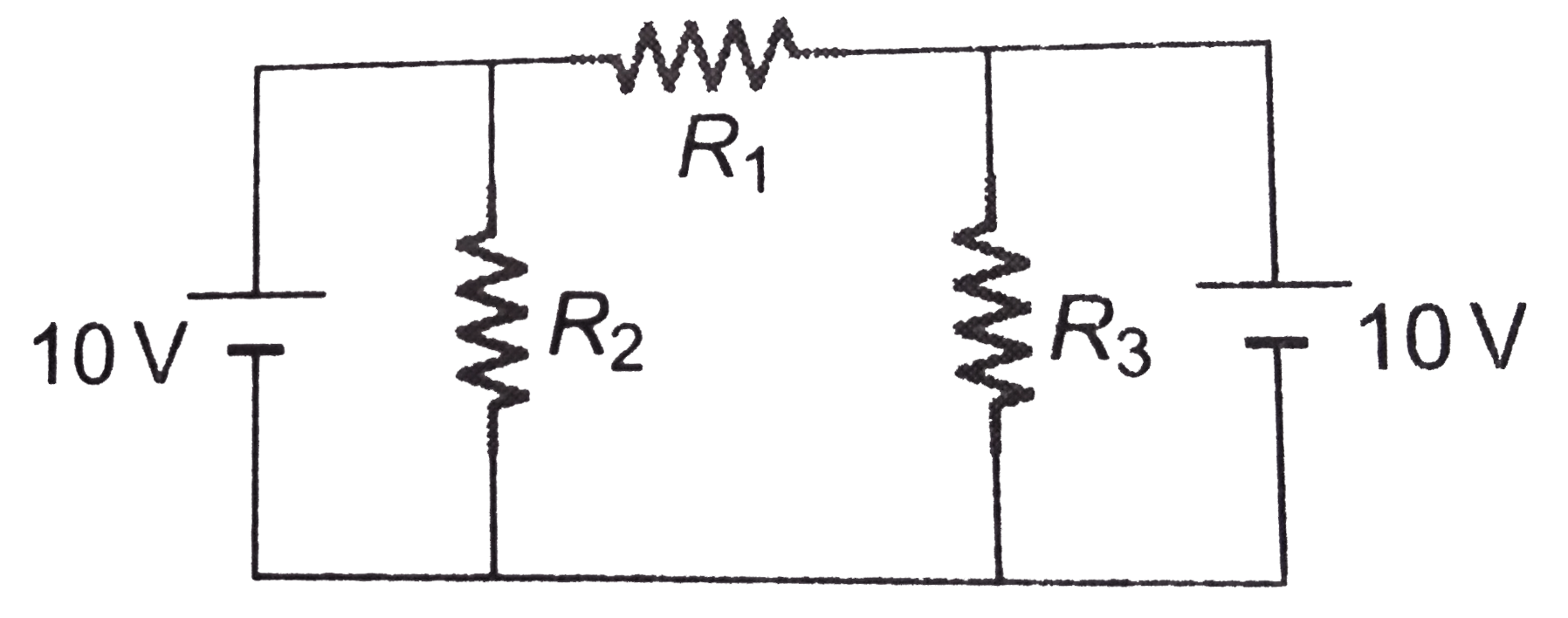
View Solution
