A particle is projected from the mid - point of the line joining two fixed particles each of mass m. If the separation between the fixed particles is l, the minimum velocity of projection of the particle so as to escape is equal to
The gravitational potential at the mid-point
The gravitational potential energy , mass of particle
When it is projected with a speed , it just escapes to infinity, and the potential and kinetic energy will become zero.

Topper's Solved these Questions
Similar Questions
A particle is projected at an angle of elevation α and after t second it appears to have an elevation of β as seen from the point of projection. Find the initial velocity of projection.
View SolutionA particle P is to be projected from a fixed point A on the ground with a fixed speed u. Another particle Q is also to be projected from a point B which is directly above the point A. The trajectory of the particle Q touches all possible trajectories (for different angle of projection) of the particle P in the vertical x−y plane. Find the equation of trajectory of the particle Q. (Take the point A as origin, horizontal axis x− axis and vertical axis y−axis Consider the figure.)

View Solution
Knowledge Check
A particle is projected from the ground with an initial speed v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectory is [EAM2013]
AucosθBu2√1+cos2θCu2√1+2cos2θDu2√1+3cos2θThe escape velocity of a particle of mass 'm'
Avaries as m2Bvaries as mCvaries as m−1Dis independent of mass
The escape velocity of a particle of mass m varies as
View SolutionA particle of mass 1kg and charge 1/3μC is projected toward a nonconducing fixed spherical shell of radius r=1mm having the same charge uniformly distributed on its surface. Find th minimum initial velocity of projection requires if the particle just grazes the shell.
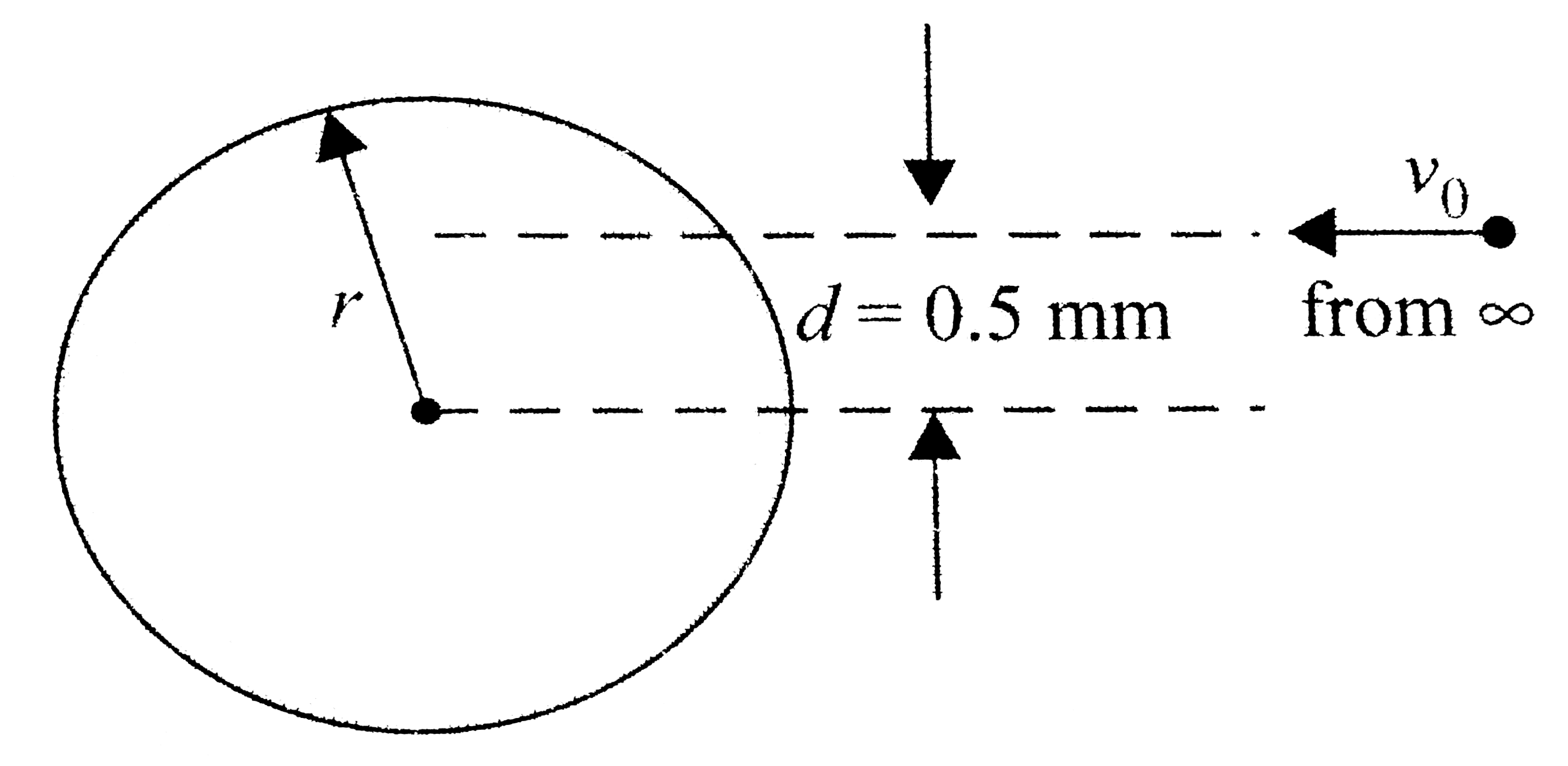 .
.
View SolutionA smooth hoop lie as on a smooth horizontal table and is fixed. A particle is projected on the table form a point A on the inner circumference of the hoop at angle θ with radius vector . If e be the coefficient of restitution and the particle returns to the point of projection after two successive impacts. The final angle θ' made by velocity vector with radius of hoop is

View SolutionA particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution
