![A closed of length l containing a liquid of variable density rho(x)=rho(0)(1+alphax) find the net force exerted by the liquid on the axis of rotation. (take the cylinder to be massless and A= cross sectional area of cylinder) (a). rho(0)Aomega^(2)l^(2)[(1)/(2)+(1)/(3)alphal] (b). rho(0)Aomega^(2)l^(2)[(1)/(2)+(2)/(3)alphal] (c). rho(0)Aomega^(2)l^(2)[(1)/(2)+alphal] (d). rho(0)Aomega^(2)l^(2)[(1)/(2)+(4)/(3)alphal]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_C08(I)_S01_064_Q01.png)
A closed of length l containing a liquid of variable density ρ(x)=ρ0(1+αx) find the net force exerted by the liquid on the axis of rotation. (take the cylinder to be massless and A= cross sectional area of cylinder)
(a). ρ0Aω2l2[12+13αl]
(b). ρ0Aω2l2[12+23αl]
(c). ρ0Aω2l2[12+αl]
(d). ρ0Aω2l2[12+43αl]
ρ0Aω2l2[12+13αl]
ρ0Aω2l2[12+23αl]
ρ0Aω2l2[12+αl]
ρ0Aω2l2[12+43αl]
∫df=∫dmω2x
⇒F=∫l0ρ0(1+αx)Adx.ω2x=ρ0Aω2∫l0(1+αx)xdx=ρ0Aω2[x22+αx33]l0
F=ρ0Aω2l2[12+αl3]

Topper's Solved these Questions
Similar Questions
Knowledge Check
A body floats in a liquid A of density ρ1 with a part of it submerged inside liquid while in liquid B of density ρ2 totally submerged inside liquid. The densities ρ1 and ρ2 are related as :
Aρ1=ρ2Bρ1<ρ2Cρ1>ρ2Dnothing can be said
A body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View SolutionA U- tube shown in Fig. containing two liquids of specific gravities ρ1 and ρ2 is given an acceleration a in the horizontal direction. What is the ratio ρ1:ρ2?
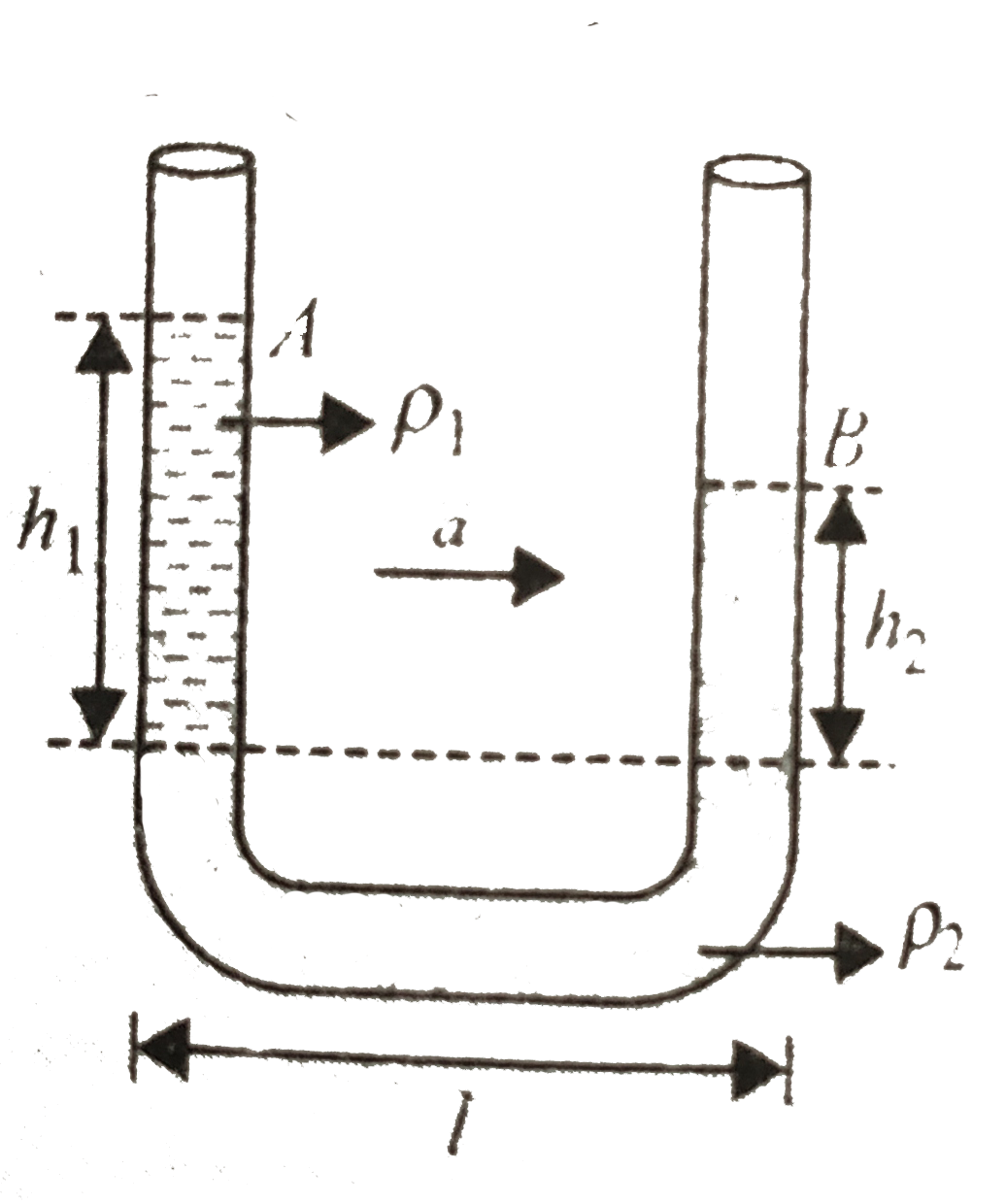
View SolutionA Solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid then density of liquid is– (r is distance from centre of sphere)
View SolutionIf two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View SolutionA rod of length L and cross section area A has variable density according to the relation ρ(x)=ρ0+kx for 0≤x≤L2 and ρ(x)=2x2 for L2≤x≤L where ρ0 and k are constants. Find the mass of the rod.
View SolutionA ball of volume V and density ρ1 is moved downwards by a distance 'd' in liquid of density ρ2. Find total change in potential energy of the system.

View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.

View Solution
