Find equivalent resistance between points A and B in the circuit shown. All resistances are equal toR.

Video Solution
Text Solution
We will solve this using symmetry about the dotted line. From this we can deduce that the centre in a branch will be equal to the current in its mirror image. For example current in AC= current in CB=i1.
This implies that even if we break the junction at C, the currents in the circuit will not be affected. Now, the circuit is simplified which can be easily solved using series parallel combination.
RAB=2R in parallel to (2R+R2)=109R
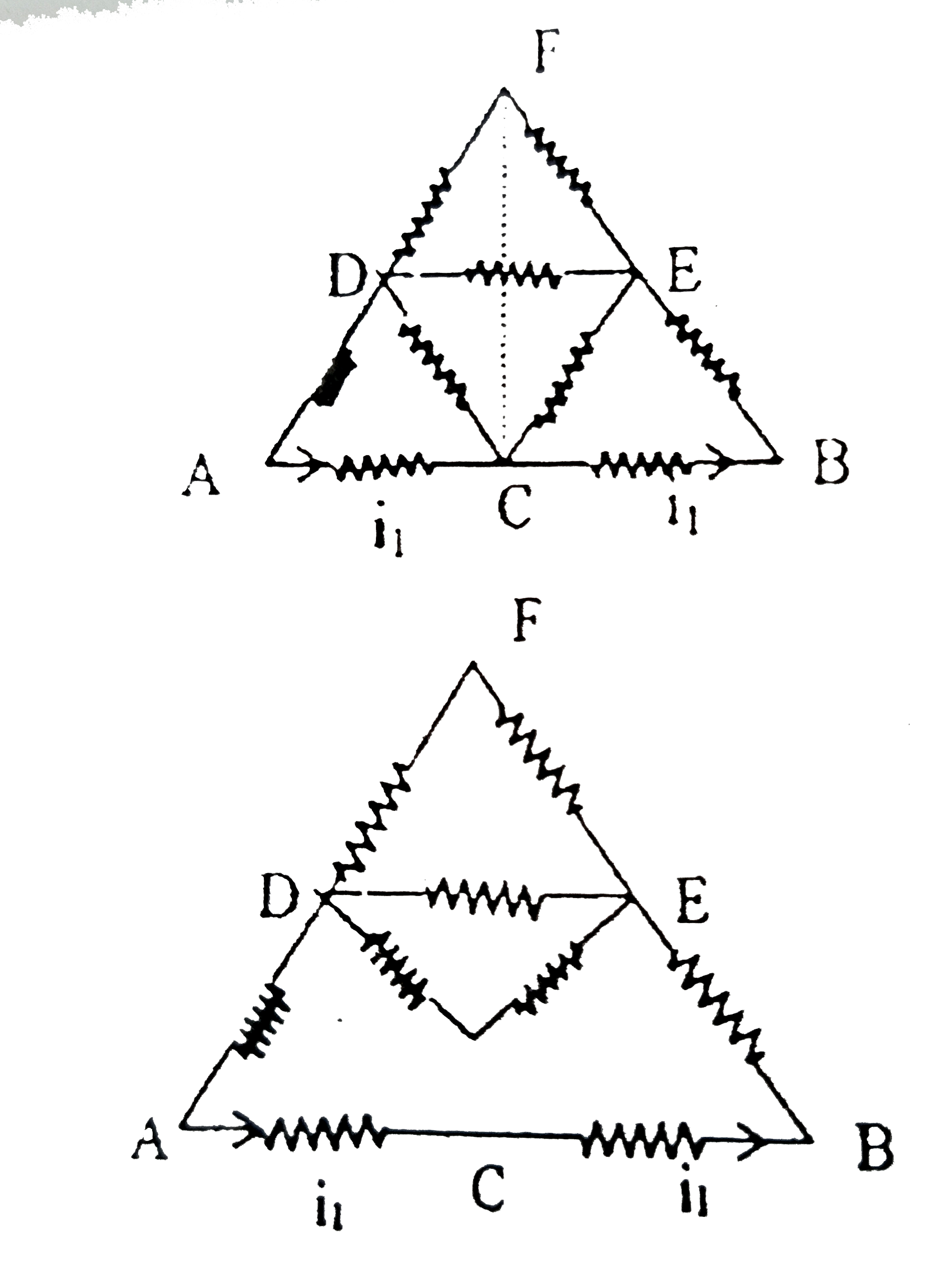
|
Similar Questions
The equivalent resistance between points A and B
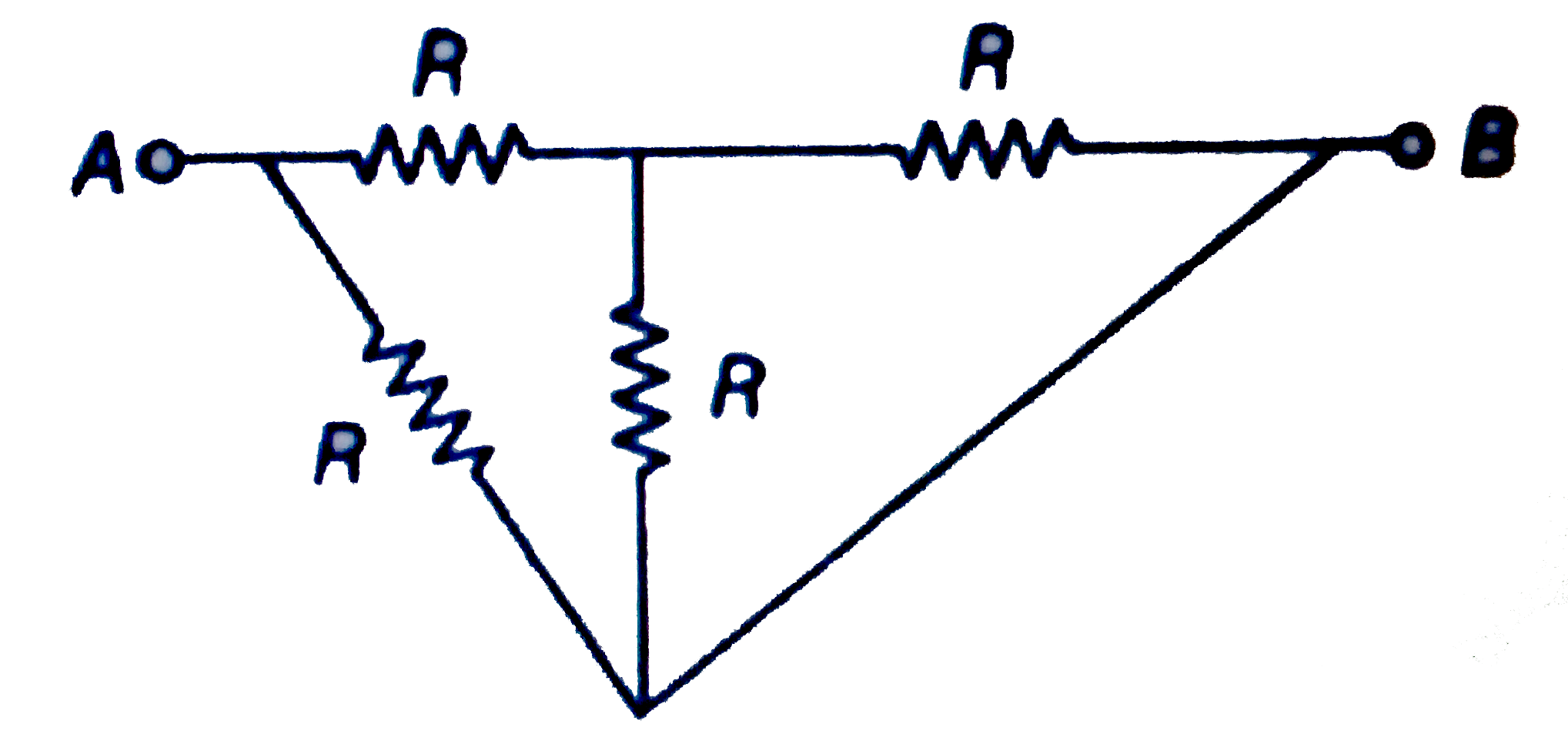
View SolutionThe equivalent resistance between points A and B

View SolutionFind the equivalent resistance between points A and B

View SolutionThe equivalent resistance between points A and B is

View SolutionThe equivalent resistance between points A and B is

View SolutionFind the equivalent resistance between points A and B.
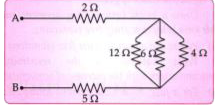
View SolutionFind the equivalent resistance between points A and B.
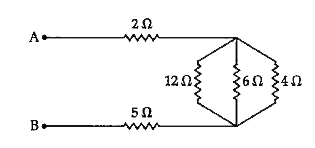
View SolutionEquivalent resistance between points A and B is
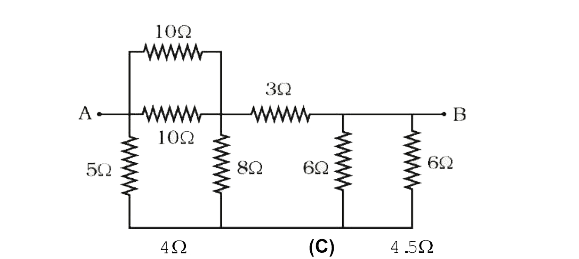
View SolutionThe equivalent resistance between point A and B in the circuit shown in figure is
_PHY_E05_041_Q01.png)
View SolutionThe equivalent resistance between points A and B in the circuit shown in figure is
_PHY_E05_095_Q01.png)
View Solution