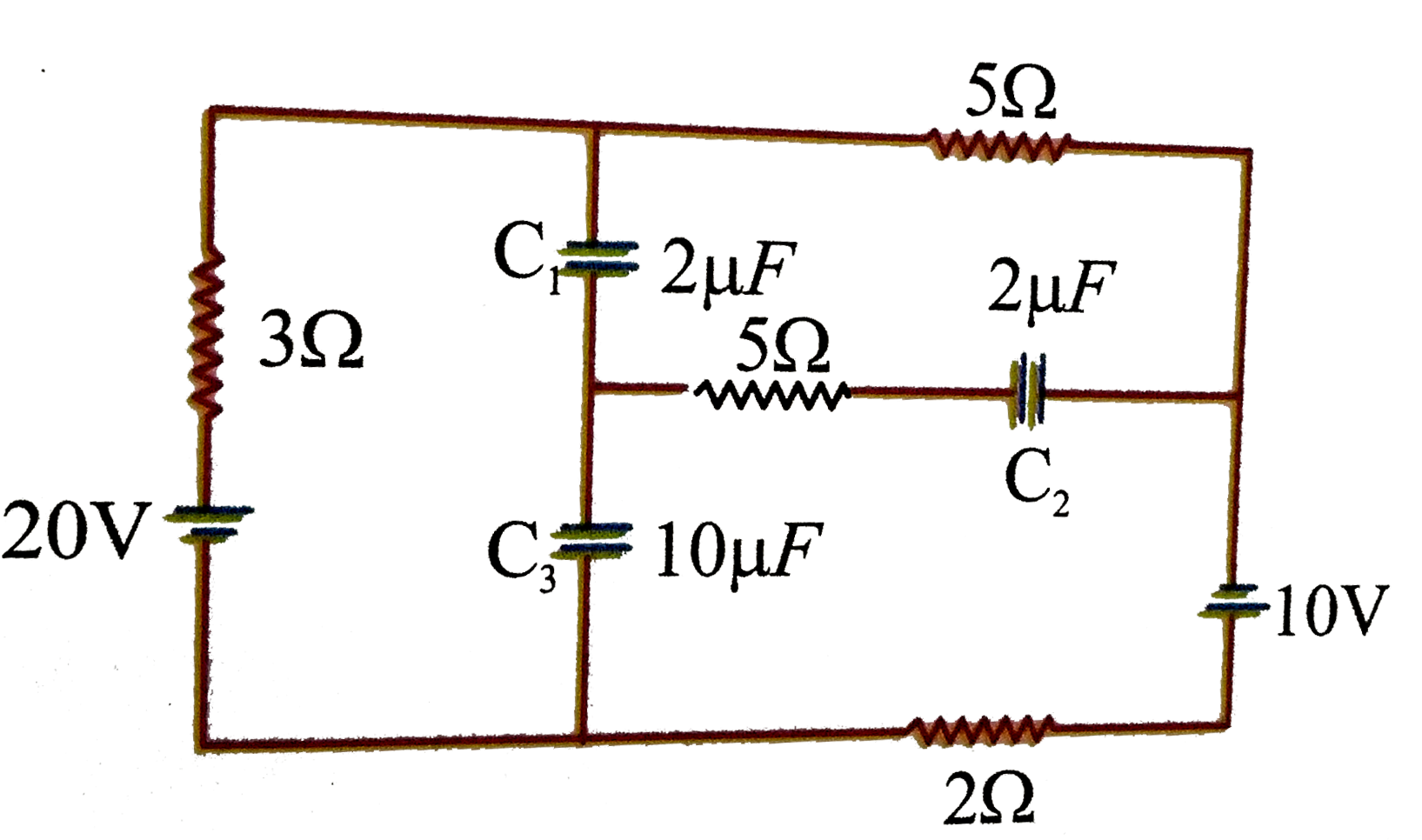
Find the charge on capacitor in steady state.
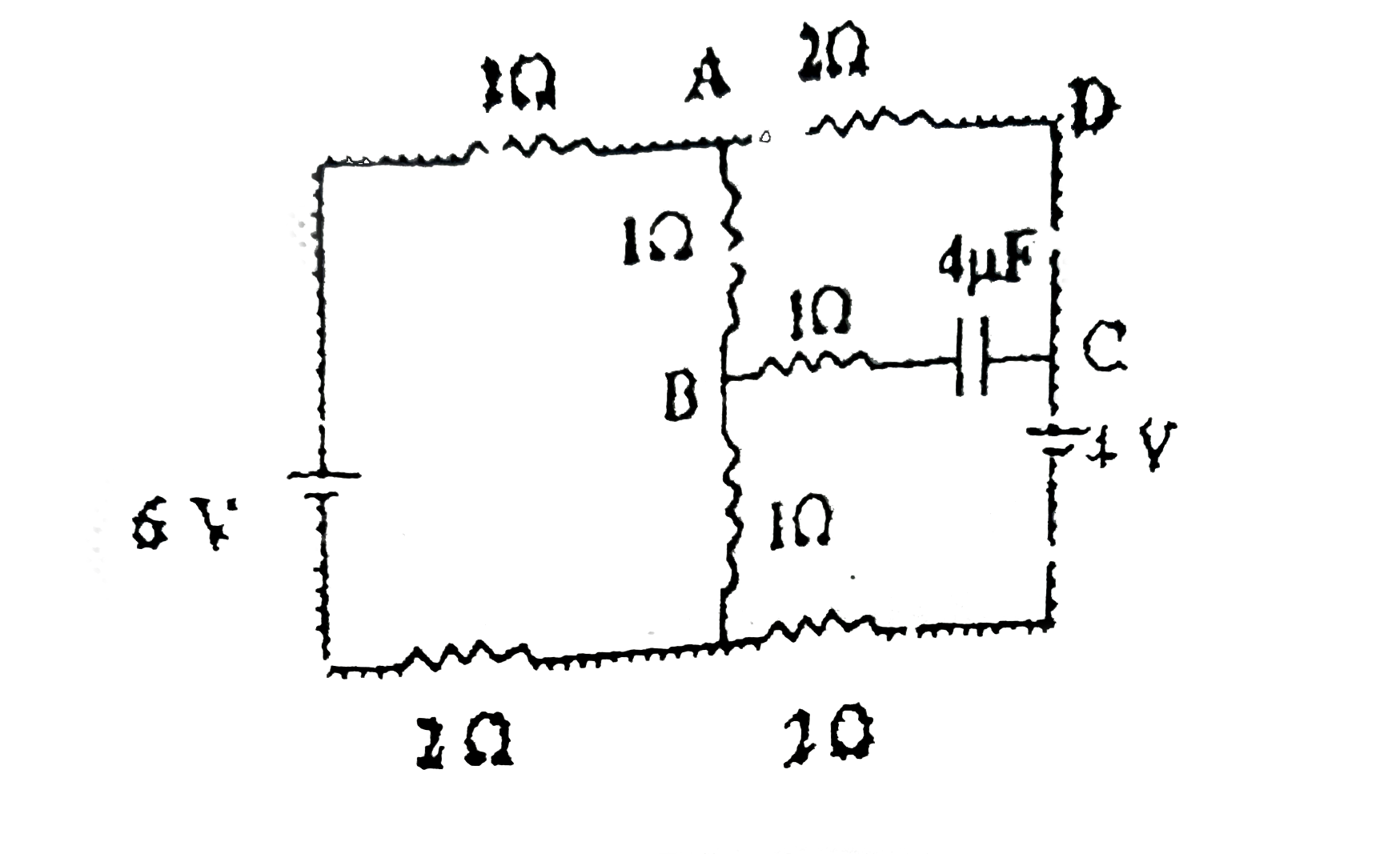
In steady state the equivalent circuit is
5i1−2i2=6
6i2−2i1=−4
13i2=14
i1=1413Amp, i2=−413 Amp
∴ Potential difference across BC
VA=6−1413=6413V
VD=6413−2(−4/13)=7213V
VB=6413−1×{1413+413}=4613V
∴VDB=72−4613=2613=2volt
∴ Charge on capacitor =CVBD=4×10−6×2=8μC

Similar Questions
For the circuit shown in the figure determine the charge on capacitor in steady state.
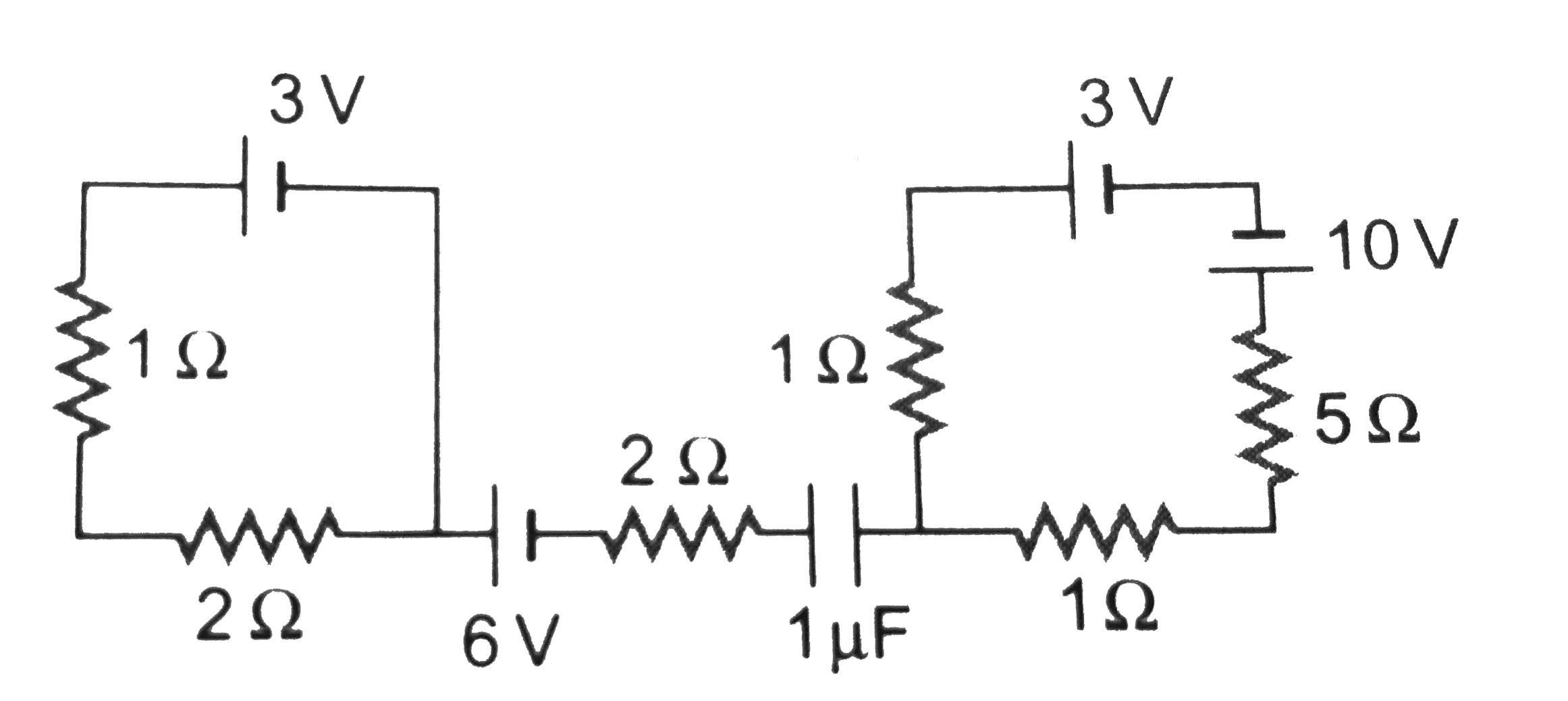
View Solution_2019_CBT3_E01_052_Q01.png)
Determine the charge on capacitor in steady state:
View SolutionFor the circuit shown in the figure, determine the charge of capacitor in steady state.
View SolutionThe circuit consists of two resistors (of resistance R1=20Ω and R2=10Ω), a capacitor (of capacitance C=10μF) and two ideal cells. In the circuit shown the capacitor is in steady state and the switch S is open
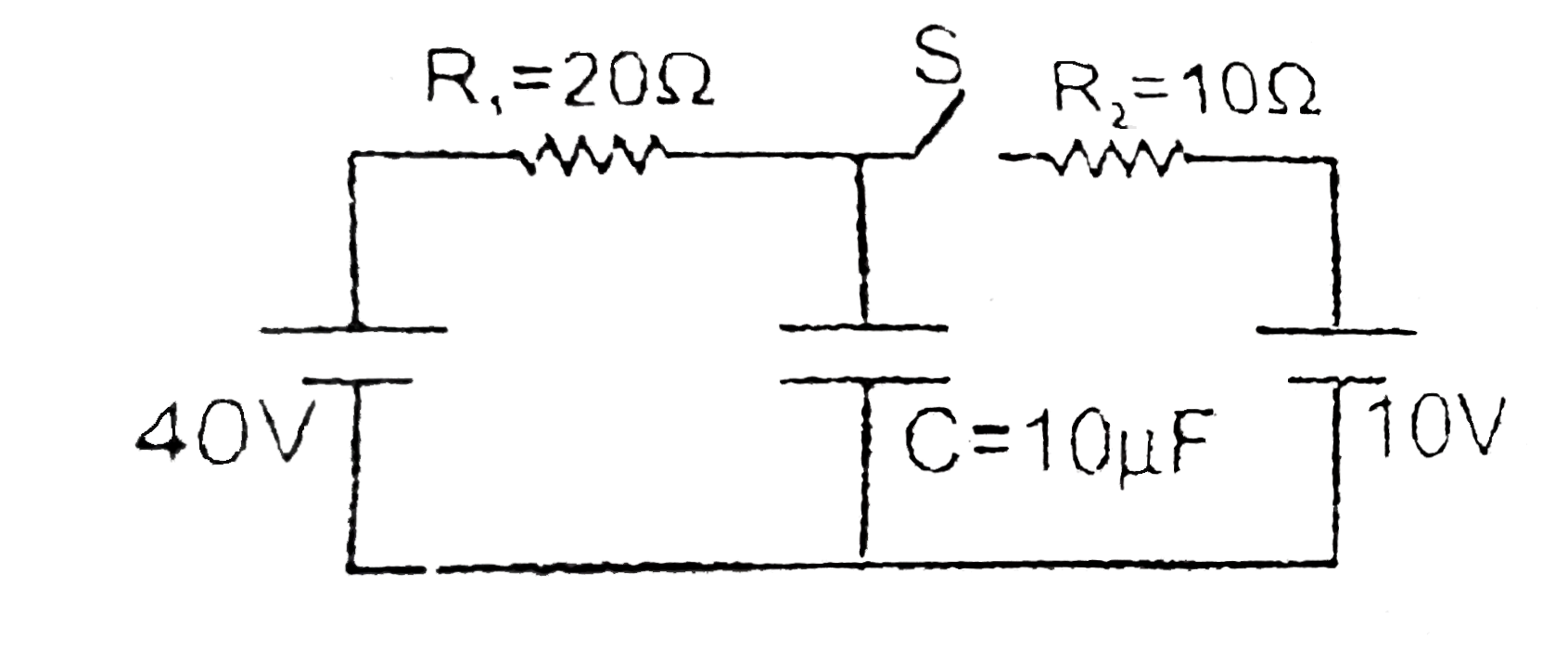
The charge on capacitor in steady state with switch S closed.
View SolutionFor the circuit shown in the figure, find the charge stored on capacitor in steady state.
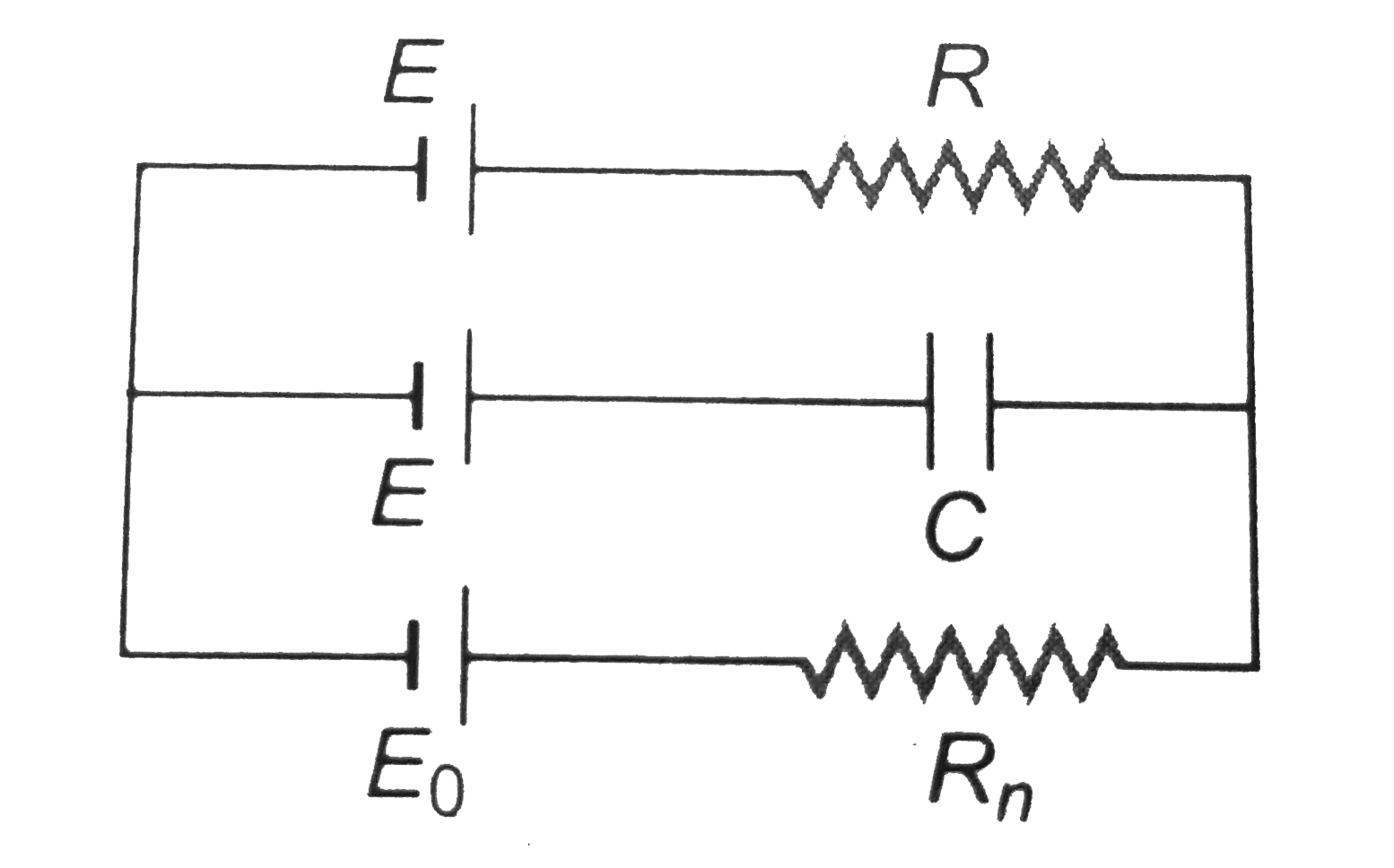
View SolutionCalculate charge on capacitor in steady state.
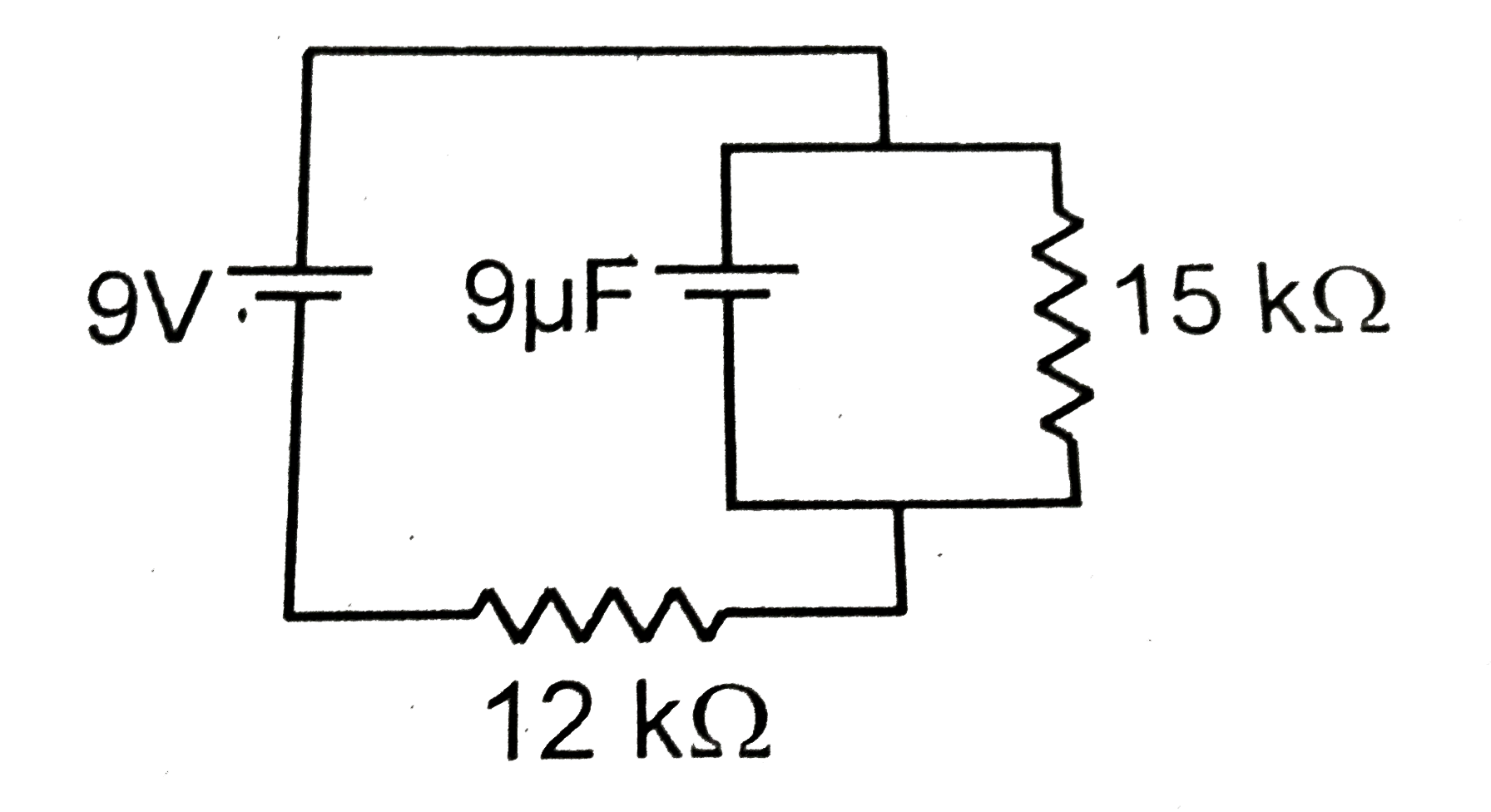
View SolutionThe charge on the capacitor in steady state in the circuit shown is
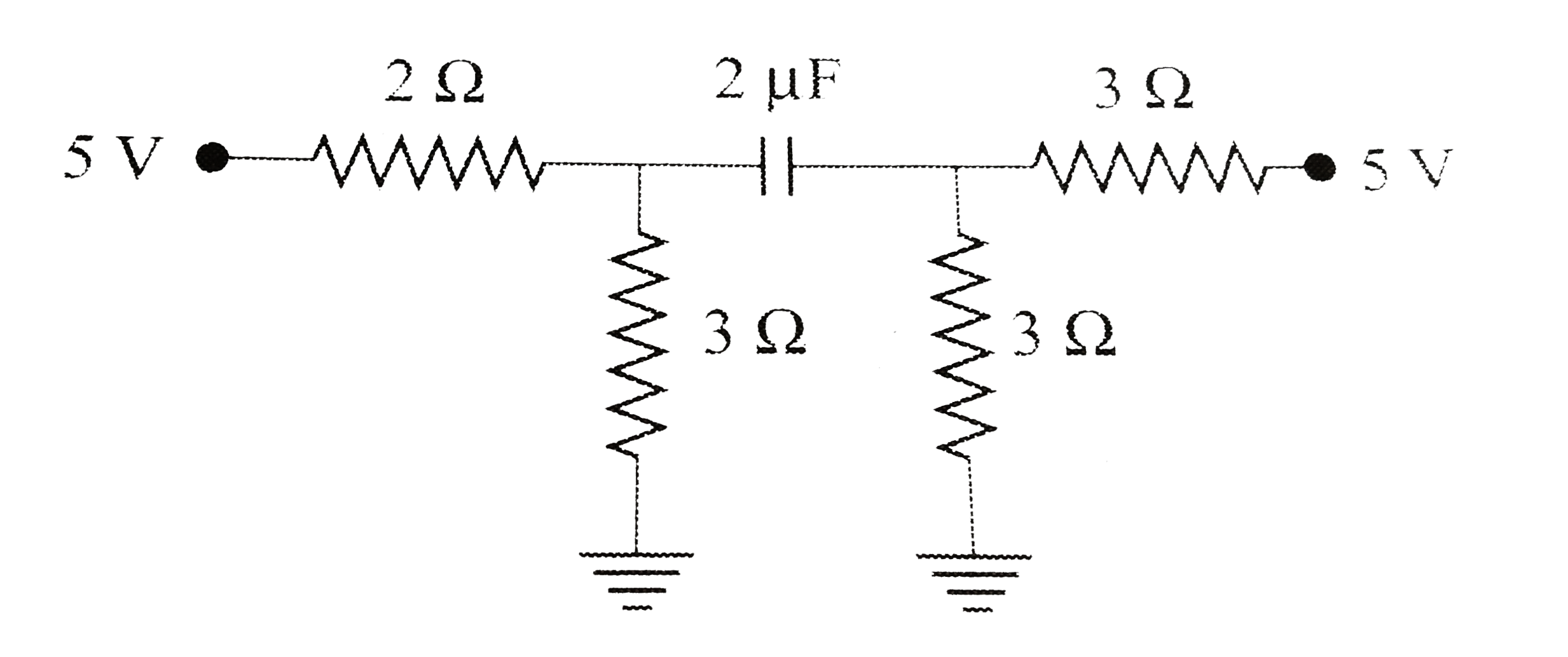
View SolutionIn the circuit shown in figure, R(1)=1Ω,R2=2Ω,C1=1μF,C2=2μF and E=6V. Calculate charge on each capacitor in steady state
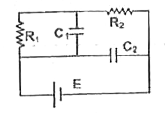
View SolutionIn the circuit shown in figure, if the charge on capacitor C2 in steady state is 10x3μC, then find value of x.
 .
.
View SolutionA capacitor of capacity 1μF is connected in a closed series circuit with a resistance or 107 ohms, an open key and a cell of 2 V with negligible internal resistance :
(i) When the key is switched on at time t=0, find,
(a) The time constant for the circuit.
(b) The charge on the capacitor at steady state.
(c) Time taken to deposit charge equal to half of charge that will deposit at steady state.
(ii) If after completely charging the capacitor, the cell is shorted by zero resistance at time t=0, find the charge on the capacitor at t=50 s. (Given : e−5=6.73×10−3,ln2=0.693)
View Solution