Write the converse of the following satement: If the two lines are parallel, then they do not intersect in the same plane.
To find the converse of the given statement, we will follow these steps:
Step 1: Identify the original statement
The original statement is: "If the two lines are parallel, then they do not intersect in the same plane."
Step 2: Break down the statement into two parts
We can denote:
- P: The two lines are parallel.
- Q: They do not intersect in the same plane.
Step 3: Write the converse
The converse of a statement of the form "If P, then Q" is "If Q, then P." However, since we want to express the converse in terms of negation, we will negate both parts:
- Negation of P: The two lines are not parallel.
- Negation of Q: They intersect in the same plane.
Step 4: Formulate the converse statement
Thus, the converse of the original statement can be written as:
"If the two lines are not parallel, then they intersect in the same plane."
Final Answer
The converse of the statement "If the two lines are parallel, then they do not intersect in the same plane" is:
"If the two lines are not parallel, then they intersect in the same plane."
---
The original statement is: "If the two lines are parallel, then they do not intersect in the same plane."
We can denote:
- P: The two lines are parallel.
- Q: They do not intersect in the same plane.
The converse of a statement of the form "If P, then Q" is "If Q, then P." However, since we want to express the converse in terms of negation, we will negate both parts:
- Negation of P: The two lines are not parallel.
- Negation of Q: They intersect in the same plane.
Thus, the converse of the original statement can be written as:
"If the two lines are not parallel, then they intersect in the same plane."
The converse of the statement "If the two lines are parallel, then they do not intersect in the same plane" is:
"If the two lines are not parallel, then they intersect in the same plane."
Similar Questions
Lines are parallel, if they do not intersect' is stated in the form of
View SolutionWrite the contrapositive and converse of the following statements.(i) If x is a prime number, then x is odd.(ii) If the two lines are parallel, then they do not intersect in the same plane, (iii) Something is cold implies that it has low temperature.(iv) You cannot comprehend geometry if you do not know how to reason deductively.(v) x is an even number implies that x is divisible by 4.
View Solution
Knowledge Check
The converse of the statement If two lines are parallel , then they do not intersect in the plane is
A1. If two lines do not intersect in the same plane then they are parallel.B2. If two lines are not parallel then they do not intersect in the same plane.C3. If two lines are not parallel then they intersect in the same plane.D4. none of the above
Write the contrapositive of the following statements: (i)If x is prime number then x is odd (ii)If two lines re parallel then they do not intersect in the same plane. (iii)x is even number implies that x is divisible by 4.
View SolutionWrite the converse of the following statements: (i)If two integers a and b are such that a>b then a−b is always a positive integer. (ii)If x is prime number, then x is odd. (iii)If two lines are parallel, then they do not intersect in the same place.
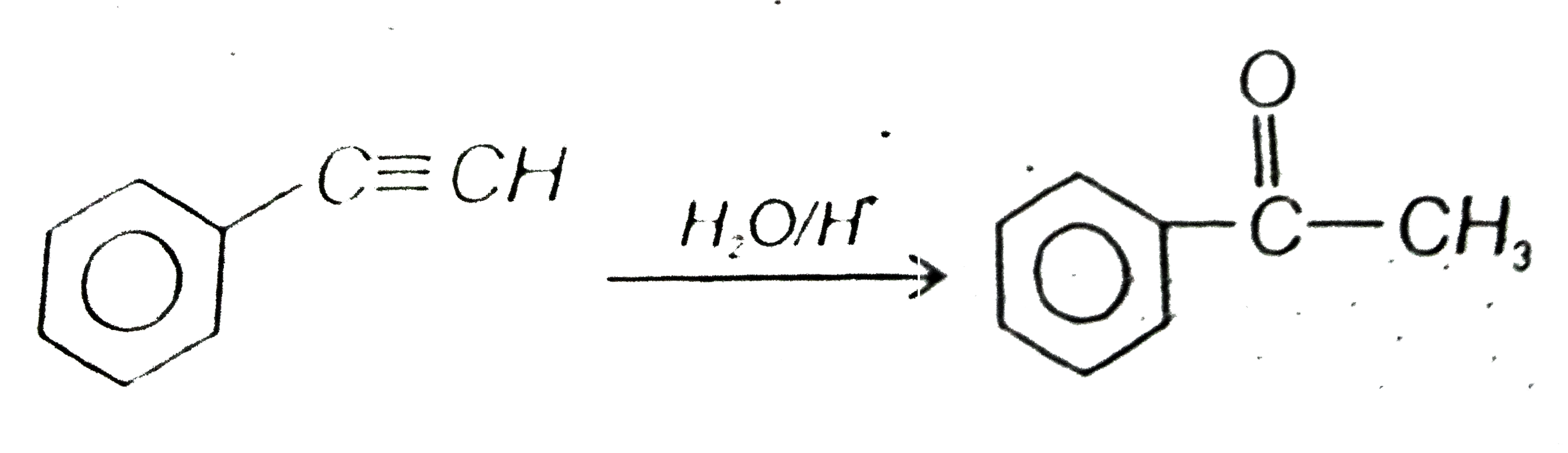
View SolutionWrite the mechanism for following conversion:
View SolutionIf there are nine straight lines of which five are concurrent at a point and the other four are concurrent at another point and no two of these nine lines are parallel, then the number of points of intersection is equal to
View SolutionWrite the negatin of each of the statement :
Two lines are parallel if and only if they have the same slope.
View SolutionState which of the following statements are true (T) or which are false (F) If two lines in the same plane do not intersect, then they must be parallel.
Distance between two parallel lines is not same everywhere.
If m⊥l, n ⊥ l and m ≠n, then mn
Two non-intersecting coplanar rays are parallel.
No two parallel segments intersect.
Every pair of lines is a pair of coplanar lines.
Two lines perpendicular to the same line are parallel.
A line perpendicular to one of two parallel lines is perpendicular to the other.
View SolutionX -axis is the intersection of two planes.
View Solution
