In a certain town 25% families own a phone and 15% own a car, 65% families own neither a phone nor a car, 2000 families own both a car and a phone . How many families live in the town ?
The correct Answer is:40,000
To solve the problem step by step, we will use the information provided about the families owning phones, cars, both, or neither.
Step 1: Define the total number of families
Let the total number of families in the town be denoted by x.
Step 2: Calculate the number of families owning a phone
According to the problem, 25% of families own a phone. Therefore, the number of families that own a phone (denoted as P) can be calculated as:
P=25100×x=0.25x
Step 3: Calculate the number of families owning a car
Similarly, 15% of families own a car. Thus, the number of families that own a car (denoted as C) is:
C=15100×x=0.15x
Step 4: Calculate the number of families owning neither a phone nor a car
The problem states that 65% of families own neither a phone nor a car. Therefore, the number of families that own neither (denoted as N) is:
N=65100×x=0.65x
Step 5: Calculate the number of families owning both a phone and a car
We are given that 2000 families own both a phone and a car. We denote this number as B:
B=2000
Step 6: Use the principle of inclusion-exclusion
According to the principle of inclusion-exclusion, the total number of families can be expressed as:
x=P+C−B+N
Substituting the values we have:
x=0.25x+0.15x−2000+0.65x
Step 7: Simplify the equation
Combining the terms on the right side:
x=(0.25+0.15+0.65)x−2000
x=1.05x−2000
Step 8: Rearranging the equation
Now, we can rearrange the equation to isolate x:
x−1.05x=−2000
−0.05x=−2000
0.05x=2000
Step 9: Solve for x
Now, divide both sides by 0.05:
x=20000.05=40000
Conclusion
Thus, the total number of families living in the town is:
40000
Let the total number of families in the town be denoted by x.
According to the problem, 25% of families own a phone. Therefore, the number of families that own a phone (denoted as P) can be calculated as:
P=25100×x=0.25x
Similarly, 15% of families own a car. Thus, the number of families that own a car (denoted as C) is:
C=15100×x=0.15x
The problem states that 65% of families own neither a phone nor a car. Therefore, the number of families that own neither (denoted as N) is:
N=65100×x=0.65x
We are given that 2000 families own both a phone and a car. We denote this number as B:
B=2000
According to the principle of inclusion-exclusion, the total number of families can be expressed as:
x=P+C−B+N
Substituting the values we have:
x=0.25x+0.15x−2000+0.65x
Combining the terms on the right side:
x=(0.25+0.15+0.65)x−2000
x=1.05x−2000
Now, we can rearrange the equation to isolate x:
x−1.05x=−2000
−0.05x=−2000
0.05x=2000
Now, divide both sides by 0.05:
x=20000.05=40000
Thus, the total number of families living in the town is:
40000
Similar Questions
In a certain town, 25% families own a phone and 15% own a car, 65% families own neither a phone nor a car. 2000 families own both a car and a phone, then
View SolutionIn a certain town 25% families own a cellphone, 15% families own a scooter and 65% families own neither a cellphone nor a scooter. If 500 families own both a cellphone and scooter, then total umber of families in the town is
View Solution
Knowledge Check
In the town of windsor, 250 families have at leat one car while 60 families have at least two cars. How many families have exactly one car?
A30B190C280D310
In a certain town 25% families own a cellphone, 15% families own a scooter and 65% families own neither a cellphone nor a scooter. If 500 families own both a cellphone and scooter, then total number of families in the town is
View SolutionA survey shows that in a city 60% familes own a car, 80% families have a scooter, and 40% have a bicycle. Also 30% own both a Car and scooter, 35% Car and bicycle and 25% scooter and bicycle, and some families owns all the three. Now the families who have neither of the three can be
View SolutionIn a town of 10000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10 % families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4 % buy a and C. If 2% families buy all the three newspaper. Find
(i) the number of families which buy newspaper A only.
(ii) the number of families which buy none of A , B and C.
View SolutionThe following bar graph gives the data about the pets owned by families in a colony.
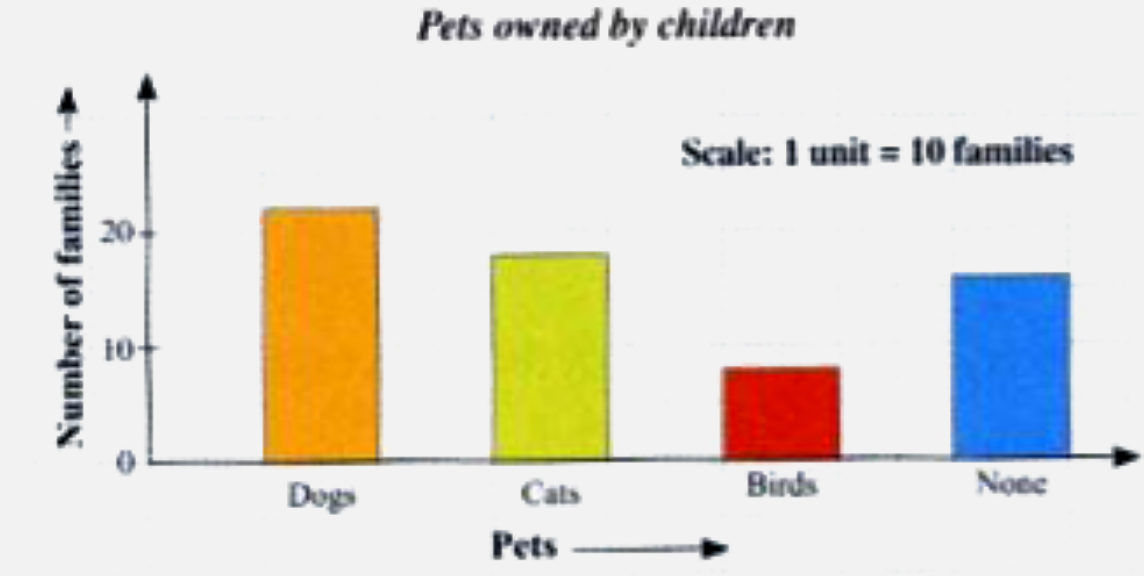
Read the graph and answer the following.
How many families do not have any pets?
View SolutionIn a certain town, 40% of the people have brown hair, 25% have brown eyes, and 15% have both brown hair and brown eyes. If a person selected at random from the town has brown hair, the probability that he also has brown eyes is 1/5 b. 3/8 c. 1/3 d. 2/3
View SolutionIn a certain city of 15000 families, 3.5% of families who read A but not B look into advertisements, 25% of the families who read B but not A look into advertisements and 50% of the families, who read both A and B look into advertisements. It is known that 8000 families read A, 4000 read B and 1000 read both A and B. The Number of families who look into advertisements are
View SolutionIn a certain city of 15000 families, 3.5% of families who read A but not B look into advertisements, 25% of the families who read B but not A look into advertisements and 50% of the families, who read both A and B look into advertisements. It is known that 8000 families read A, 4000 read B and 1000 read both A and B. The number of families who read none of the newspaper are
View Solution