In a certain town 25% families own a cellphone, 15% families own a scooter and 65% families own neither a cellphone nor a scooter. If 500 families own both a cellphone and scooter, then total umber of families in the town is
10000
20000
30000
40000
The correct Answer is:C
To solve the problem step by step, we will use the information provided about the families in the town.
Step 1: Define the Variables
Let x be the total number of families in the town.
Step 2: Calculate the Percentages
From the problem, we know:
- 25% of families own a cellphone:
n(A)=25100×x=25x100
- 15% of families own a scooter:
n(B)=15100×x=15x100
- 65% of families own neither a cellphone nor a scooter:
n(neither)=65100×x
Step 3: Calculate Families Owning Either or Both
Since 65% own neither, the percentage of families that own either a cellphone or a scooter (or both) is:
n(A∪B)=x−n(neither)=x−65100x=35100x
Step 4: Use the Information About Families Owning Both
We are given that 500 families own both a cellphone and a scooter:
n(A∩B)=500
Step 5: Apply the Formula for Union of Two Sets
Using the formula for the union of two sets:
n(A∪B)=n(A)+n(B)−n(A∩B)
Substituting the values we have:
35100x=25100x+15100x−500
Step 6: Simplify the Equation
Combine the terms on the right:
35100x=40100x−500
Step 7: Rearranging the Equation
Rearranging gives:
35100x−40100x=−500
−5100x=−500
Step 8: Solve for x
Multiplying both sides by -1:
5100x=500
Now, multiply both sides by 100:
5x=50000
Finally, divide by 5:
x=10000
Final Answer
The total number of families in the town is 10000.
Let x be the total number of families in the town.
From the problem, we know:
- 25% of families own a cellphone:
n(A)=25100×x=25x100
- 15% of families own a scooter:
n(B)=15100×x=15x100
- 65% of families own neither a cellphone nor a scooter:
n(neither)=65100×x
Since 65% own neither, the percentage of families that own either a cellphone or a scooter (or both) is:
n(A∪B)=x−n(neither)=x−65100x=35100x
We are given that 500 families own both a cellphone and a scooter:
n(A∩B)=500
Using the formula for the union of two sets:
n(A∪B)=n(A)+n(B)−n(A∩B)
Substituting the values we have:
35100x=25100x+15100x−500
Combine the terms on the right:
35100x=40100x−500
Rearranging gives:
35100x−40100x=−500
−5100x=−500
Multiplying both sides by -1:
5100x=500
Now, multiply both sides by 100:
5x=50000
Finally, divide by 5:
x=10000
The total number of families in the town is 10000.
Topper's Solved these Questions
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Section I - Solved Mcqs
24 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test
59 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Chapter Test
34 Videos
Similar Questions
In a certain town, 25% families own a phone and 15% own a car, 65% families own neither a phone nor a car. 2000 families own both a car and a phone, then
View SolutionIn a certain town 25% families own a phone and 15% own a car, 65% families own neither a phone nor a car, 2000 families own both a car and a phone . How many families live in the town ?
View Solution
Knowledge Check
Tamark Street has 30 families, each family owns dogs amongst three different breeds - Alsatian, Spitz ad Golden - retriever . A family , can have dogs of multiple breeds but at most one dog of any breed. There are 11 families having an Alsation and 14 families having a Spitz. There are 10 families who dogs of exactly two different breeds and 2 families own dogs of all three breeds. What is the total number of dogs on Tamarak street ?
A30B35C36D44
A survey shows that in a city 60% familes own a car, 80% families have a scooter, and 40% have a bicycle. Also 30% own both a Car and scooter, 35% Car and bicycle and 25% scooter and bicycle, and some families owns all the three. Now the families who have neither of the three can be
View SolutionIn a town of 10000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10 % families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4 % buy a and C. If 2% families buy all the three newspaper. Find
(i) the number of families which buy newspaper A only.
(ii) the number of families which buy none of A , B and C.
View SolutionIn a certain city of 15000 families, 3.5% of families who read A but not B look into advertisements, 25% of the families who read B but not A look into advertisements and 50% of the families, who read both A and B look into advertisements. It is known that 8000 families read A, 4000 read B and 1000 read both A and B. The Number of families who look into advertisements are
View SolutionIn a certain city of 15000 families, 3.5% of families who read A but not B look into advertisements, 25% of the families who read B but not A look into advertisements and 50% of the families, who read both A and B look into advertisements. It is known that 8000 families read A, 4000 read B and 1000 read both A and B. The number of families who read none of the newspaper are
View SolutionIn a certain town, 40% of the people have brown hair, 25% have brown eyes, and 15% have both brown hair and brown eyes. If a person selected at random from the town has brown hair, the probability that he also has brown eyes is 1/5 b. 3/8 c. 1/3 d. 2/3
View SolutionIn a town of 10,000 families it was found that 40% family buy newspaper A, 20% buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2%families buy all the three newspapers, then find the number of families which buy A only
View SolutionThe following bar graph gives the data about the pets owned by families in a colony.
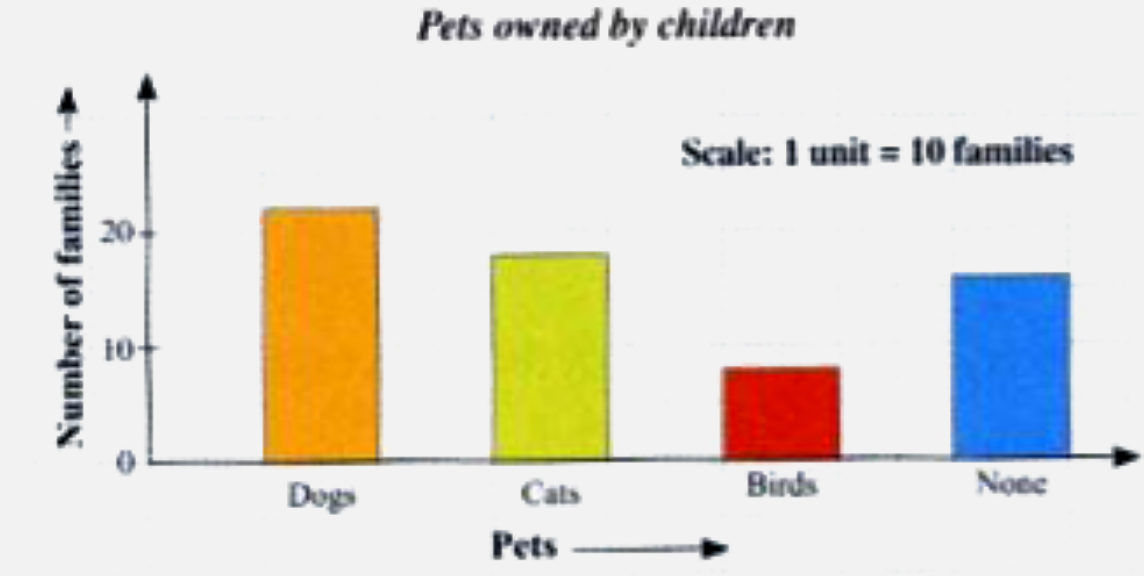
Read the graph and answer the following.
How many families do not have any pets?
View Solution
