Intensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
A) E=(14πε0)λr
B) E=(14πε0)2λr
C) E=(14πε0)λr2
D) E=(14πε0)2λr2
The correct Answer is:B
To find the intensity of the electric field at a point at a perpendicular distance r from an infinite line charge with linear charge density λ, we can use Gauss's Law. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have an infinite line charge with a linear charge density λ. We want to find the electric field intensity E at a distance r from this line charge.
Step 2: Choose a Gaussian Surface
To apply Gauss's Law, we choose a cylindrical Gaussian surface of radius r and length L that is coaxial with the line charge. The symmetry of the problem suggests that the electric field will be uniform and directed radially outward from the line charge.
Step 3: Apply Gauss's Law
Gauss's Law states:
ΦE=∮→E⋅d→A=qenclosedϵ0
where ΦE is the electric flux through the Gaussian surface, qenclosed is the charge enclosed by the surface, and ϵ0 is the permittivity of free space.
Step 4: Calculate the Electric Flux
The electric field E is constant over the curved surface of the cylinder, and there is no contribution from the ends of the cylinder (the electric field is perpendicular to the area vector at those points). Thus, the electric flux through the curved surface is:
ΦE=E⋅(2πrL)
where 2πrL is the surface area of the curved side of the cylinder.
Step 5: Calculate the Charge Enclosed
The charge enclosed by the Gaussian surface is given by:
qenclosed=λ⋅L
where λ is the linear charge density.
Step 6: Substitute into Gauss's Law
Substituting the expressions for electric flux and charge enclosed into Gauss's Law gives:
E⋅(2πrL)=λLϵ0
Step 7: Solve for Electric Field E
Now, we can solve for E:
E=λ2πϵ0r
Conclusion
Thus, the intensity of the electric field at a point at a perpendicular distance r from an infinite line charge with linear charge density λ is given by:
E=λ2πϵ0r
We have an infinite line charge with a linear charge density λ. We want to find the electric field intensity E at a distance r from this line charge.
To apply Gauss's Law, we choose a cylindrical Gaussian surface of radius r and length L that is coaxial with the line charge. The symmetry of the problem suggests that the electric field will be uniform and directed radially outward from the line charge.
Gauss's Law states:
ΦE=∮→E⋅d→A=qenclosedϵ0
where ΦE is the electric flux through the Gaussian surface, qenclosed is the charge enclosed by the surface, and ϵ0 is the permittivity of free space.
The electric field E is constant over the curved surface of the cylinder, and there is no contribution from the ends of the cylinder (the electric field is perpendicular to the area vector at those points). Thus, the electric flux through the curved surface is:
ΦE=E⋅(2πrL)
where 2πrL is the surface area of the curved side of the cylinder.
The charge enclosed by the Gaussian surface is given by:
qenclosed=λ⋅L
where λ is the linear charge density.
Substituting the expressions for electric flux and charge enclosed into Gauss's Law gives:
E⋅(2πrL)=λLϵ0
Now, we can solve for E:
E=λ2πϵ0r
Thus, the intensity of the electric field at a point at a perpendicular distance r from an infinite line charge with linear charge density λ is given by:
E=λ2πϵ0r
Similar Questions
Intensity of electric field at a perpendicular distance of 0.5 m from an infinitely long line charge having linear charge density (λ) is 3.6×103Vm−1 . Find the value of λ
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View SolutionThe dimensional formula of linear charge density λ is
View SolutionFind the electric flux crossing the wire frame ABCD of length l, width b, and center at a distance OP = d from an infinite line of charge with linear charge density λ. Consider that the plane of the frame is perpendicular to the line OP

View SolutionTwo infinite line charges with uniform linear charge densities +λ&−λ are kept in such a way that the angle between them is 30∘. The electric field at the symmetric point P at a perpendicular distance r from each line charge is given by:
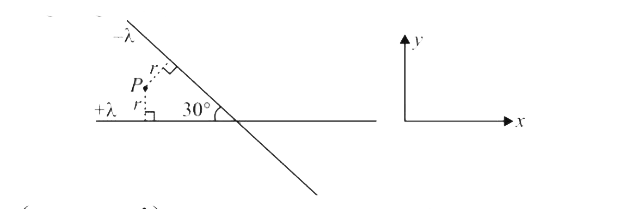
View SolutionTwo infinite line charges with uniform linear charge densities +λ&−λ are kept in such a way that the angle between them is 30∘. The electric field at the symmetric point P at a perpendicular distance r from each line charge is given by:

View SolutionLet E1(r), E2(r) and E3(r) be the respectively electric field at a distance r from a point charge Q, an infinitely long wire with constant linear charge density λ, and an infinite plane with uniform surface charge density σ. If E1(r0)=E2(r0)=E3(r0) at a given distance r0, then
View SolutionElectric field at centre O of semicircule of radius 'a' having linear charge density λ given is given by

View SolutionThe magnitude electric potential difference between A and B for a given infinite line charge having uniform density λ is approximately (Given loge2=0.7 , λ=10−8Cm)
View Solution