Two concentric shells of radii R and 2R are shown in the figure. Initially a charge q is imparted to the inner shell. After the keys $K_{1} & K_{2}$ are alternately closed n times each, find the potential difference between the shells.

Video Solution

Text Solution

Verified by Experts

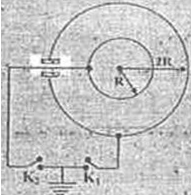
When $K_{1}$ is closed first time, outer sphere is earthed and its potential becomes zero. Let the charge on it be $q_{1}$ .
$V_{1}$ '= Potential due to charge on inner sphere and that due to charge on outer sphere.
$0 = \frac{1}{4 π ε_{0}} [\frac{q}{2 R} + \frac{q_{1}}{2 R}]$
$\Rightarrow q_{1}' = q$
When $K_{2}$ is closed first time, the potential $V_{2}'$ on inner sphere becomes zero as it is earthed.
Let the new charge on inner sphere be $q_{2}$ '
$0 = \frac{1}{4 π ε_{0}} \frac{q_{2}}{R} + \frac{1}{4 π ε_{0}} \frac{(- q)}{(2 R)}$
$\Rightarrow q_{2}' = q / 2$
Now when $K_{1}$ will be closed second time charge on outer sphere will be $- q_{2}$ ' i.e. $- q / 2$
Similarly when $K_{1}$ will be closed nth time, charge on outer sphere will be $- \frac{q}{2^{n - 1}}$ as each time.
Charge will be reduced to half the previous value.
After closing $K_{2}$ nth time charge on inner shell will be negative to half the charge on outer shell.
i.e. $(- \frac{q}{2^{n}})$ and potential on it will be zero.
For potential of outer shell
$V_{0} = \frac{1}{4 π ε_{0}} \frac{(- q / 2^{n})}{2 R} + \frac{1}{4 π ε_{0}} \frac{(\frac{q}{2^{n - 1}})}{2 R}$
$V_{0} = \frac{q [- 1 + 2]}{4 π ε_{0} 2^{n + 1} R} = + \frac{q}{4 π ε_{0} 2^{n + 1} R}$
Potential difference = $V_{0} - V_{1} = \frac{q}{4 π ε_{0} 2^{n + 1} R} - 0 = \frac{q}{4 π ε_{0} 2^{n + 1} R}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile