A spherical Gaussian surface surrounds a point charge q. If the charge is moved to another location inside the surface? Then total flux_____________
To solve the question, we will apply Gauss's Law, which relates the electric flux through a closed surface to the charge enclosed by that surface.
1. Understanding Gauss's Law:
Gauss's Law states that the total electric flux (Φ) through a closed surface is equal to the charge (q) enclosed by that surface divided by the permittivity of free space (ε₀). Mathematically, it is expressed as:
Φ=qenclosedϵ0
2. Identifying the Scenario:
In this problem, we have a spherical Gaussian surface that surrounds a point charge q. Initially, the charge is at a certain position inside the Gaussian surface.
3. Moving the Charge:
The problem states that the charge q is moved to another location inside the same Gaussian surface. It is important to note that even though the position of the charge changes, the total charge enclosed by the Gaussian surface remains the same.
4. Applying Gauss's Law:
Since the charge q is still enclosed by the Gaussian surface after being moved, we can use Gauss's Law again:
Φ=qϵ0
Here, q is still the same charge, and ϵ0 is a constant.
5. Conclusion:
Therefore, the total electric flux through the Gaussian surface remains unchanged regardless of the position of the charge inside the surface. The total flux is determined solely by the amount of charge enclosed.
Final Answer:
The total flux remains the same.
---
Gauss's Law states that the total electric flux (Φ) through a closed surface is equal to the charge (q) enclosed by that surface divided by the permittivity of free space (ε₀). Mathematically, it is expressed as:
Φ=qenclosedϵ0
In this problem, we have a spherical Gaussian surface that surrounds a point charge q. Initially, the charge is at a certain position inside the Gaussian surface.
The problem states that the charge q is moved to another location inside the same Gaussian surface. It is important to note that even though the position of the charge changes, the total charge enclosed by the Gaussian surface remains the same.
Since the charge q is still enclosed by the Gaussian surface after being moved, we can use Gauss's Law again:
Φ=qϵ0
Here, q is still the same charge, and ϵ0 is a constant.
Therefore, the total electric flux through the Gaussian surface remains unchanged regardless of the position of the charge inside the surface. The total flux is determined solely by the amount of charge enclosed.
The total flux remains the same.
Similar Questions
Consider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
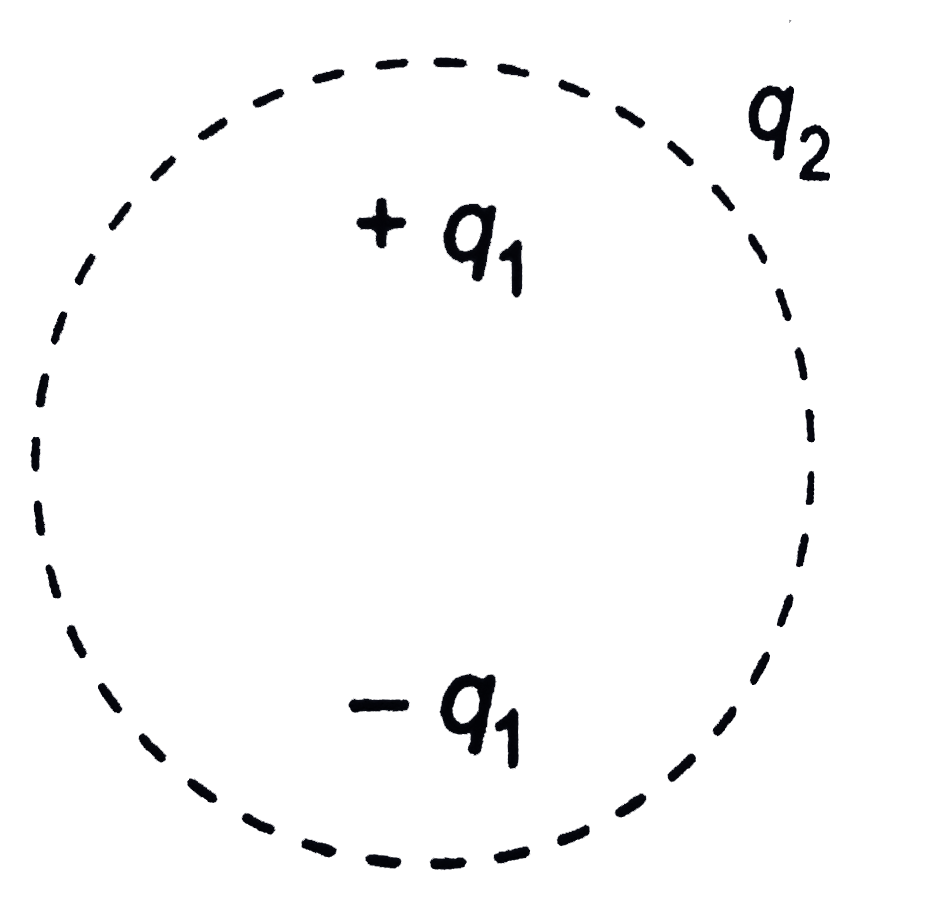
View SolutionConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.

View SolutionA point charge causes an electric flux of −1.0×103Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface ? (b) What is the is the value of the point charge ?
View SolutionA point charge causes an electric flux of −1.0×103Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface ? (b) What is the is the value of the point charge ?
View SolutionConsider a Gaussian spherical surface covering a dipole of charge q and -q, then

View SolutionIf net flux through a Gaussian surface is zero, then find whether the following statements are correct or not.
The net charge inside the surface is zero.
View SolutionFind the total flux due to charge q associated with the given hemispherical surface
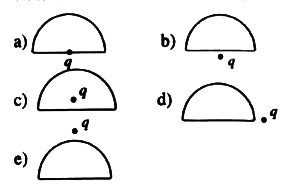
View SolutionStatement-1 : A hollow metallic sphere of inner radius a and outer radius b has charge q at the centre. A negatively charged moves from inner surface outer surface. Then total work done will be zero.
Statement-2: Potential is constant inside the metallic sphere.
View SolutionA point charge is placed at the centre of spherical Gaussian surface. Is electric flux ϕE changed if
(a) The sphere is replaced by a cube of same or different volume ?
(b) The charge is moved off-centre in the original sphere, still remaining inside ?
( c ) The charge is moved just outside the original sphere ?
(d) A second charge is placed near the outside to the origianl sphere ?
(e) A second charge is placed inside the Gaussian surface ?
View SolutionWhen a 10 μC charge is enclosed by a closed surface, the flux passing through the surface is ϕ. Now another 10 µC charge is placed inside the closed surface, then the flux passing through the surface is ______.
View Solution
