A conducting ball is given a certain charge and fixed at point P. An another point charge of mass 1 gm and charge 20μC when kept at Q (3m, 9m) starts moving with acceleration →a=(1.08ˆi+1.44ˆj)ms−2. The potential at Q is +720 volt. Calculate charge given to ball
To solve the problem step by step, we will use the given information about the charges, potential, and acceleration to find the charge given to the conducting ball.
Step 1: Understand the Given Information
- Mass of the point charge m=1g=0.001kg
- Charge of the point charge Q2=20μC=20×10−6C
- Acceleration →a=(1.08^i+1.44^j)m/s2
- Electric potential at point Q VQ=720V
Step 2: Calculate the Force Acting on the Charge
Using Newton's second law, the force F acting on the charge can be calculated as:
F=m⋅a
Substituting the values:
F=0.001kg⋅(1.08^i+1.44^j)m/s2
Calculating the magnitude of the force:
F=0.001⋅√(1.082+1.442)N
Calculating √(1.082+1.442):
=√(1.1664+2.0736)=√3.24≈1.8N
Thus,
F≈0.001⋅1.8=0.0018N
Step 3: Relate Force to Electric Field
The force on the charge Q2 due to the electric field E is given by:
F=Q2⋅E
Thus, we can express the electric field as:
E=FQ2
Substituting the values:
E=0.0018N20×10−6C=0.00180.00002=90N/C
Step 4: Relate Electric Field to Potential
The electric field E is related to the potential V by the equation:
E=−dVdr
In this case, the potential VQ at point Q is given, and we can express the potential due to the charge Q1 at point P as:
VQ=k⋅Q1r
where k is Coulomb's constant (8.99×109N m2/C2).
Step 5: Calculate Charge Q1
From the potential equation:
VQ=k⋅Q1r
We can rearrange this to find Q1:
Q1=VQ⋅rk
We also know that the electric field E can be expressed in terms of Q1 as:
E=k⋅Q1r2
Setting the two expressions for E equal gives:
90=k⋅Q1r2
Now we can substitute r from VQ:
r=k⋅Q1VQ
Substituting r into the equation for E:
90=k⋅Q1(k⋅Q1VQ)2
Solving this will give us Q1.
Final Calculation
After substituting and simplifying, we find:
Q1=V2Q⋅Q2k⋅m⋅a
Substituting the known values:
Q1=(720)2⋅(20×10−6)(8.99×109)⋅(0.001)⋅(1.8)
Calculating this gives:
Q1≈6.4×10−7C
Conclusion
The charge given to the conducting ball is approximately 6.4×10−7C.
- Mass of the point charge m=1g=0.001kg
- Charge of the point charge Q2=20μC=20×10−6C
- Acceleration →a=(1.08^i+1.44^j)m/s2
- Electric potential at point Q VQ=720V
Using Newton's second law, the force F acting on the charge can be calculated as:
F=m⋅a
Substituting the values:
F=0.001kg⋅(1.08^i+1.44^j)m/s2
Calculating the magnitude of the force:
F=0.001⋅√(1.082+1.442)N
Calculating √(1.082+1.442):
=√(1.1664+2.0736)=√3.24≈1.8N
Thus,
F≈0.001⋅1.8=0.0018N
The force on the charge Q2 due to the electric field E is given by:
F=Q2⋅E
Thus, we can express the electric field as:
E=FQ2
Substituting the values:
E=0.0018N20×10−6C=0.00180.00002=90N/C
The electric field E is related to the potential V by the equation:
E=−dVdr
In this case, the potential VQ at point Q is given, and we can express the potential due to the charge Q1 at point P as:
VQ=k⋅Q1r
where k is Coulomb's constant (8.99×109N m2/C2).
From the potential equation:
VQ=k⋅Q1r
We can rearrange this to find Q1:
Q1=VQ⋅rk
We also know that the electric field E can be expressed in terms of Q1 as:
E=k⋅Q1r2
Setting the two expressions for E equal gives:
90=k⋅Q1r2
Now we can substitute r from VQ:
r=k⋅Q1VQ
Substituting r into the equation for E:
90=k⋅Q1(k⋅Q1VQ)2
Solving this will give us Q1.
After substituting and simplifying, we find:
Q1=V2Q⋅Q2k⋅m⋅a
Substituting the known values:
Q1=(720)2⋅(20×10−6)(8.99×109)⋅(0.001)⋅(1.8)
Calculating this gives:
Q1≈6.4×10−7C
The charge given to the conducting ball is approximately 6.4×10−7C.
Similar Questions
The potential at a point 0.1 m from an isolated point charge is + 100 volt. The nature of the point charge is
View SolutionFind out potential energy of the two point charge system having charges q1 and q2 separated by distance r.
View SolutionFind out electric field intensity at point A (0, 1m, 2m) due to a point charge −20μC situated at point B(√2m,0,1m).
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionA positive charge .Q. is fixed at a point, A negatively charged of mass .m. and charge .q. is revolving in a circular path of radius radius r1 with .Q. as the centre. The change in potential energy to change the radius of the circular path from r1andr2 in joule is
View SolutionWhat work is required to bring a charge q=3.00μC originally a distance of 1.50 m from a charge Q=20.0μC until it is 0.50 m away ?
View SolutionA point charge q1=q is placed at point P. Another point charge q2=−q is placed at point Q. At some point R(R≠P,R≠Q), electric potential due to q−1isV1 and electric potential due to q2 is V2. Which of the following is correct
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View SolutionFind out the points on the line joining two charges +qand−3q(kept at as distance of 1.0m) where electric potential is zero.
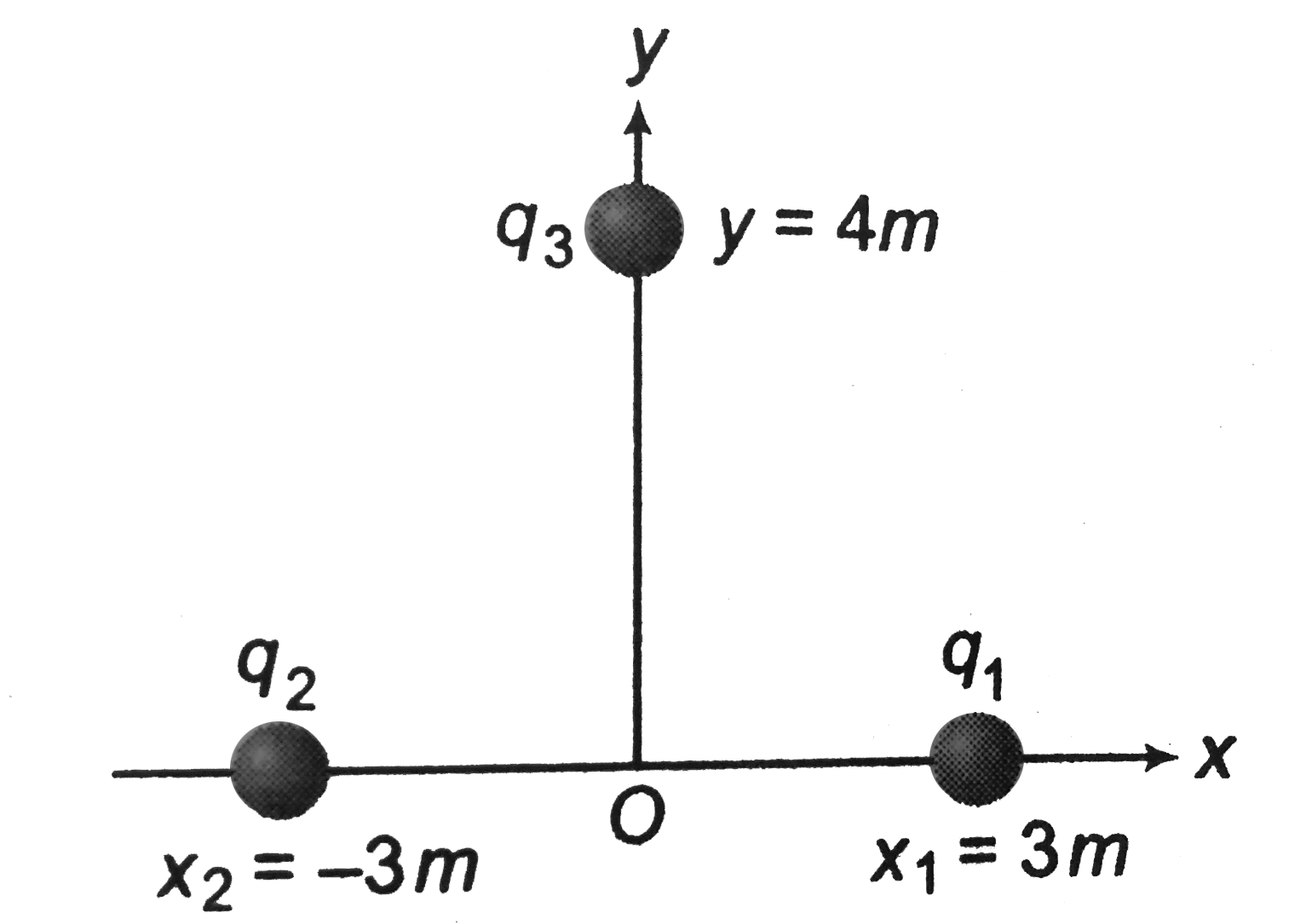
View SolutionTwo point charges q1=q2=2μC are fixed at x1=+3m and x2=−3m as shown in figure. A third particle of mass 1 g and charge q3=−4μC are released from rest at y=4.0m.Find the speed of the particle as it reaches the origin.
 View Solution
View Solution

