Figure shows three concentric thin spherical shells A, B and C of radii a, b, and c. The shells A and C are given charge q and -q, respectively, and shell B is earthed. Then,
the charge q will be there at outer surface A
the charge −bqc will be there at inner surface of C
the charge −q will be at inner surface of B
the charge q(1−b/c) will be there at outer surface of C
The correct Answer is:A, B, C
To solve the problem regarding the three concentric spherical shells A, B, and C, we will analyze the charge distribution and electric potential step by step.
Step 1: Understanding the Configuration
We have three concentric spherical shells:
- Shell A with radius a and charge +q
- Shell B with radius b which is earthed (potential = 0)
- Shell C with radius c and charge −q
Step 2: Electric Field Inside the Conductors
Since A, B, and C are conductors, the electric field inside each conductor must be zero. Therefore, the charge on each shell will redistribute itself such that the electric field inside each shell is null.
Step 3: Charge Distribution on Shell B
Since shell B is earthed, its potential must be zero. The potential at shell B due to the charges on shells A and C must balance out to maintain this condition.
Step 4: Potential at Shell B
The potential VB at shell B due to shell A and shell C can be expressed as:
VB=VA+VC
Where:
- VA=q4πϵ0b (due to shell A)
- VC=−q4πϵ0b+Q′4πϵ0b (due to shell C and the induced charge Q′ on shell B)
Setting VB=0:
q4πϵ0b+(−q+Q′4πϵ0b)=0
Step 5: Solving for Induced Charge on Shell B
From the equation above, we can simplify:
q+Q′−q4πϵ0b=0
This leads to:
Q′=−qbc
Thus, the charge induced on the inner surface of shell B is −Q′=qbc.
Step 6: Charge on the Outer Surface of Shell C
The charge on the outer surface of shell C can be calculated as:
Qouter_C=−q+Q′=−q+qbc
This simplifies to:
Qouter_C=q(bc−1)
Step 7: Charge on the Inner Surface of Shell C
The charge on the inner surface of shell C will be the negative of the charge induced on shell B:
Qinner_C=−Q′=−qbc
Final Charge Distribution Summary
1. Charge on the outer surface of shell A: +q
2. Charge on the inner surface of shell B: −qbc
3. Charge on the inner surface of shell C: −qbc
4. Charge on the outer surface of shell C: q(bc−1)
Conclusion
Based on the calculations:
- The charge on the outer surface of shell A is +q (Correct).
- The charge on the inner surface of shell C is −qbc (Correct).
- The charge on the inner surface of shell B is −q (Correct).
- The charge on the outer surface of shell C is q(bc−1) (Incorrect).
We have three concentric spherical shells:
- Shell A with radius a and charge +q
- Shell B with radius b which is earthed (potential = 0)
- Shell C with radius c and charge −q
Since A, B, and C are conductors, the electric field inside each conductor must be zero. Therefore, the charge on each shell will redistribute itself such that the electric field inside each shell is null.
Since shell B is earthed, its potential must be zero. The potential at shell B due to the charges on shells A and C must balance out to maintain this condition.
The potential VB at shell B due to shell A and shell C can be expressed as:
VB=VA+VC
Where:
- VA=q4πϵ0b (due to shell A)
- VC=−q4πϵ0b+Q′4πϵ0b (due to shell C and the induced charge Q′ on shell B)
q4πϵ0b+(−q+Q′4πϵ0b)=0
From the equation above, we can simplify:
q+Q′−q4πϵ0b=0
This leads to:
Q′=−qbc
Thus, the charge induced on the inner surface of shell B is −Q′=qbc.
The charge on the outer surface of shell C can be calculated as:
Qouter_C=−q+Q′=−q+qbc
This simplifies to:
Qouter_C=q(bc−1)
The charge on the inner surface of shell C will be the negative of the charge induced on shell B:
Qinner_C=−Q′=−qbc
1. Charge on the outer surface of shell A: +q
2. Charge on the inner surface of shell B: −qbc
3. Charge on the inner surface of shell C: −qbc
4. Charge on the outer surface of shell C: q(bc−1)
Based on the calculations:
- The charge on the outer surface of shell A is +q (Correct).
- The charge on the inner surface of shell C is −qbc (Correct).
- The charge on the inner surface of shell B is −q (Correct).
- The charge on the outer surface of shell C is q(bc−1) (Incorrect).
Similar Questions
Figure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View SolutionFour concentric conducting spherical shells A, B, C and D of radii a, 2a, 3a and 4a respectively. Shell B and D are given charges q and −q respectively. If shell C is grounded then potential difference (VA — VC) is
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionFigure shows three concentric conducting spherical shells of radii a,b and c (c>b>a) . The innermost and outermost shell are given charge sQ1 and Q2 respectively, and the middle shell had been earthed. Select the correct alternative(s) .
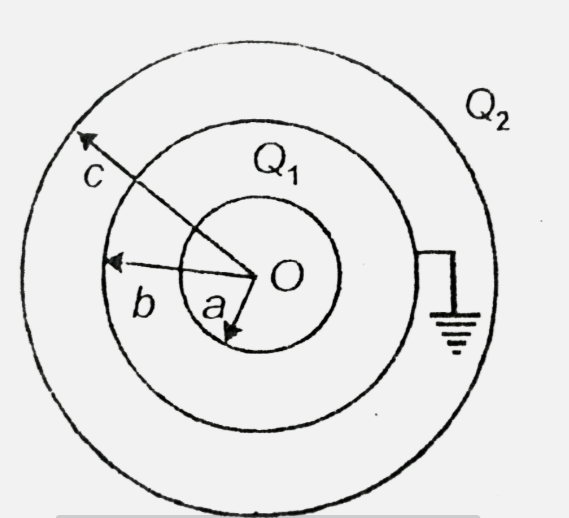
View Solution(Figure 3.78) shows three thin concentric spherical shells A, B and C with initial charges on A , B, and C as 3 Q, 2Q, and -Q, respectively. The shells A amd C are connected by a wire such that it does not touch B. Shell B is earthed. Determine the final charges qA,qB,andqC.
 .
.
View Solution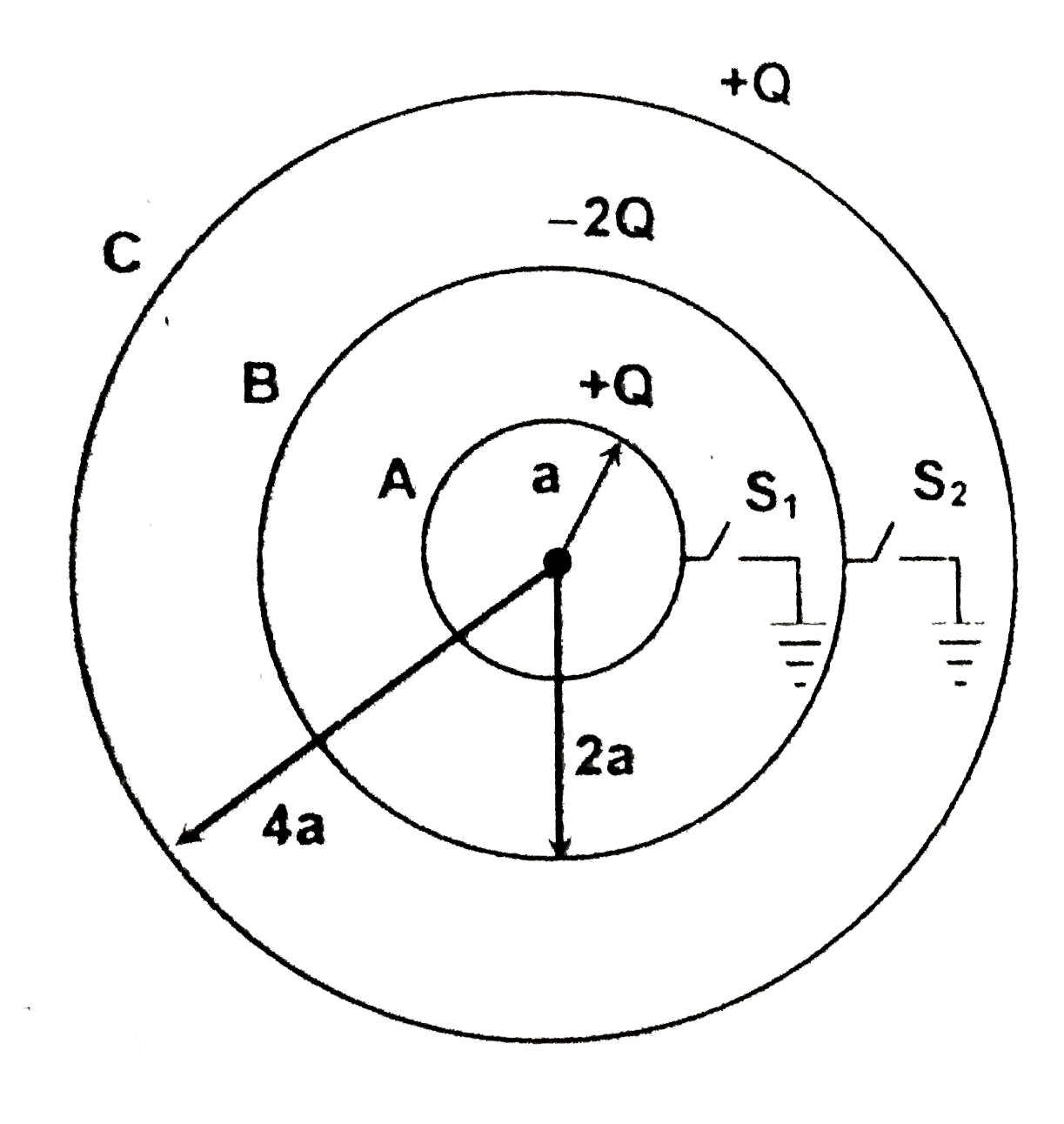
Three concentric spherical conducting shells A, B and C of radii a, 2a and 4a are initially given charges +Q, -2Q and +Q respectively. The charge on the middle spherical shell B after switches S1 and S2 are simultaneously closed, will be
View Solution