There are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
kq2a
kq4a
kq4a
kq6a
The correct Answer is:D
To solve the problem step by step, we will analyze the potential at different shells due to the charges on the other shells.
Step 1: Understand the Configuration
We have four concentric shells A, B, C, and D with radii a, 2a, 3a, and 4a respectively. Shell B has a charge of +q, shell D has a charge of −q, and shell C is earthed (potential = 0).
Step 2: Calculate the Potential at Shell A
The potential at shell A (VA) is due to the charges on shells B, C, and D. The formula for the potential V due to a shell of charge Q at a distance r from its center is given by:
V=kQr
where k=14πϵ0.
1. Potential due to shell B at radius 2a:
VB=kq2a
2. Potential due to shell C (which is earthed, so it has a charge QC that we will find later):
VC=kQC3a
3. Potential due to shell D at radius 4a:
VD=−kq4a
Combining these, the total potential at shell A is:
VA=kq2a+kQC3a−kq4a
Step 3: Calculate the Potential at Shell C
Since shell C is earthed, its potential VC is:
VC=0
Step 4: Solve for QC
Since VC=0, we can express the potential at shell C:
0=kq3a+kQC3a−kq4a
Multiplying through by 3a to eliminate the denominators:
0=q+QC−3q4
Rearranging gives:
QC=−q+3q4=−q4
Step 5: Substitute QC Back into VA
Now substituting QC=−q4 back into the expression for VA:
VA=kq2a+k−q43a−kq4a
Calculating each term:
1. The first term: kq2a
2. The second term: k−q43a=−kq12a
3. The third term: −kq4a
Combining these:
VA=k(q2a−q12a−3q12a)
=k(6q12a−4q12a)=k2q12a=kq6a
Step 6: Calculate the Potential Difference VA−VC
Since VC=0:
VA−VC=VA−0=VA=kq6a
Final Result
The potential difference VA−VC is:
VA−VC=kq6a
We have four concentric shells A, B, C, and D with radii a, 2a, 3a, and 4a respectively. Shell B has a charge of +q, shell D has a charge of −q, and shell C is earthed (potential = 0).
The potential at shell A (VA) is due to the charges on shells B, C, and D. The formula for the potential V due to a shell of charge Q at a distance r from its center is given by:
V=kQr
where k=14πϵ0.
VB=kq2a
VC=kQC3a
VD=−kq4a
VA=kq2a+kQC3a−kq4a
Since shell C is earthed, its potential VC is:
VC=0
Since VC=0, we can express the potential at shell C:
0=kq3a+kQC3a−kq4a
Multiplying through by 3a to eliminate the denominators:
0=q+QC−3q4
Rearranging gives:
QC=−q+3q4=−q4
Now substituting QC=−q4 back into the expression for VA:
VA=kq2a+k−q43a−kq4a
Calculating each term:
1. The first term: kq2a
2. The second term: k−q43a=−kq12a
3. The third term: −kq4a
VA=k(q2a−q12a−3q12a)
=k(6q12a−4q12a)=k2q12a=kq6a
Since VC=0:
VA−VC=VA−0=VA=kq6a
The potential difference VA−VC is:
VA−VC=kq6a
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE6videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.110videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Objective82videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Four concentric conducting spherical shells A, B, C and D of radii a, 2a, 3a and 4a respectively. Shell B and D are given charges q and −q respectively. If shell C is grounded then potential difference (VA — VC) is
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b, and c. The shells A and C are given charge q and -q, respectively, and shell B is earthed. Then,
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.
 View Solution
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.
 View Solution
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
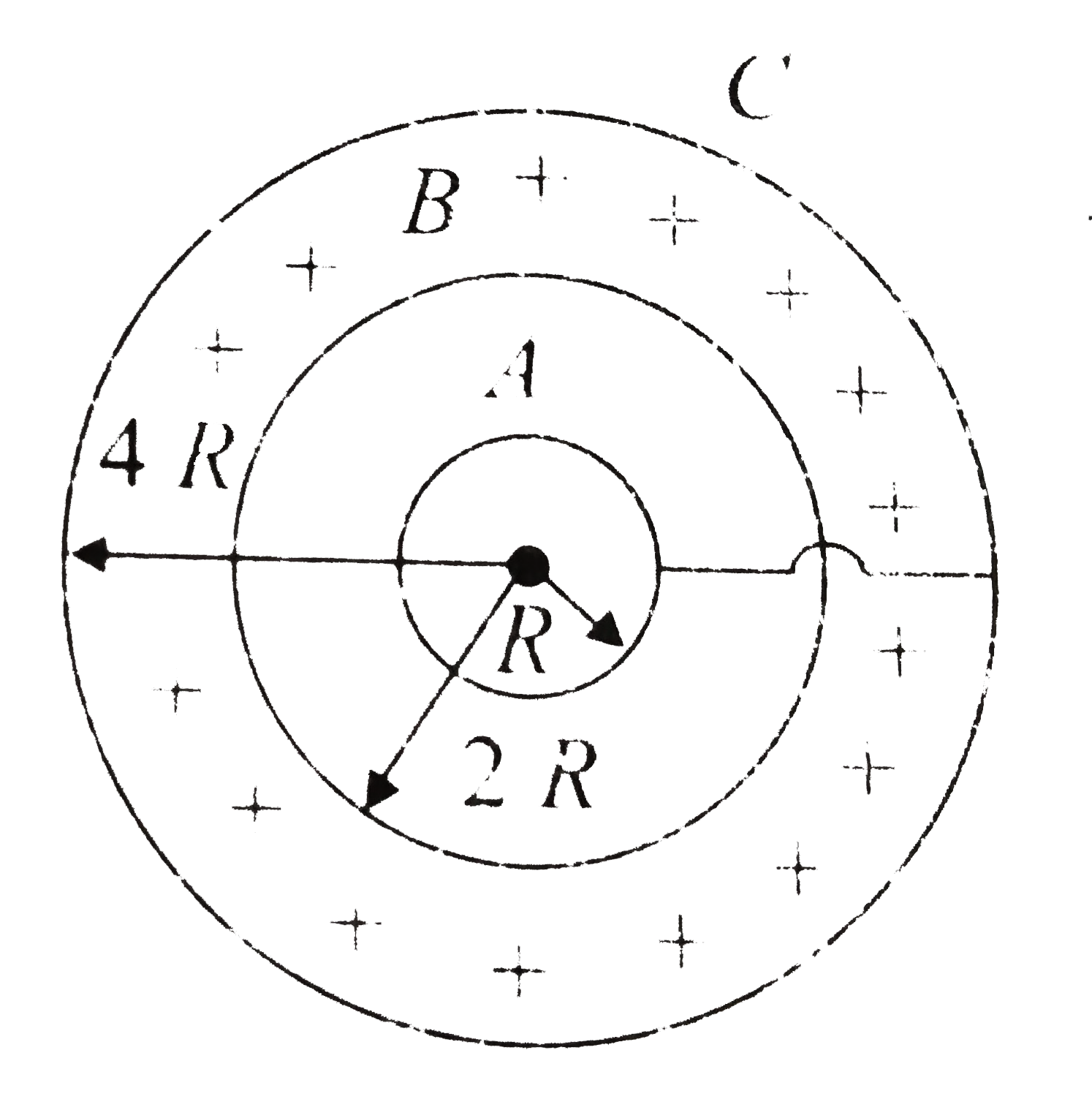
Potential at B isView SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
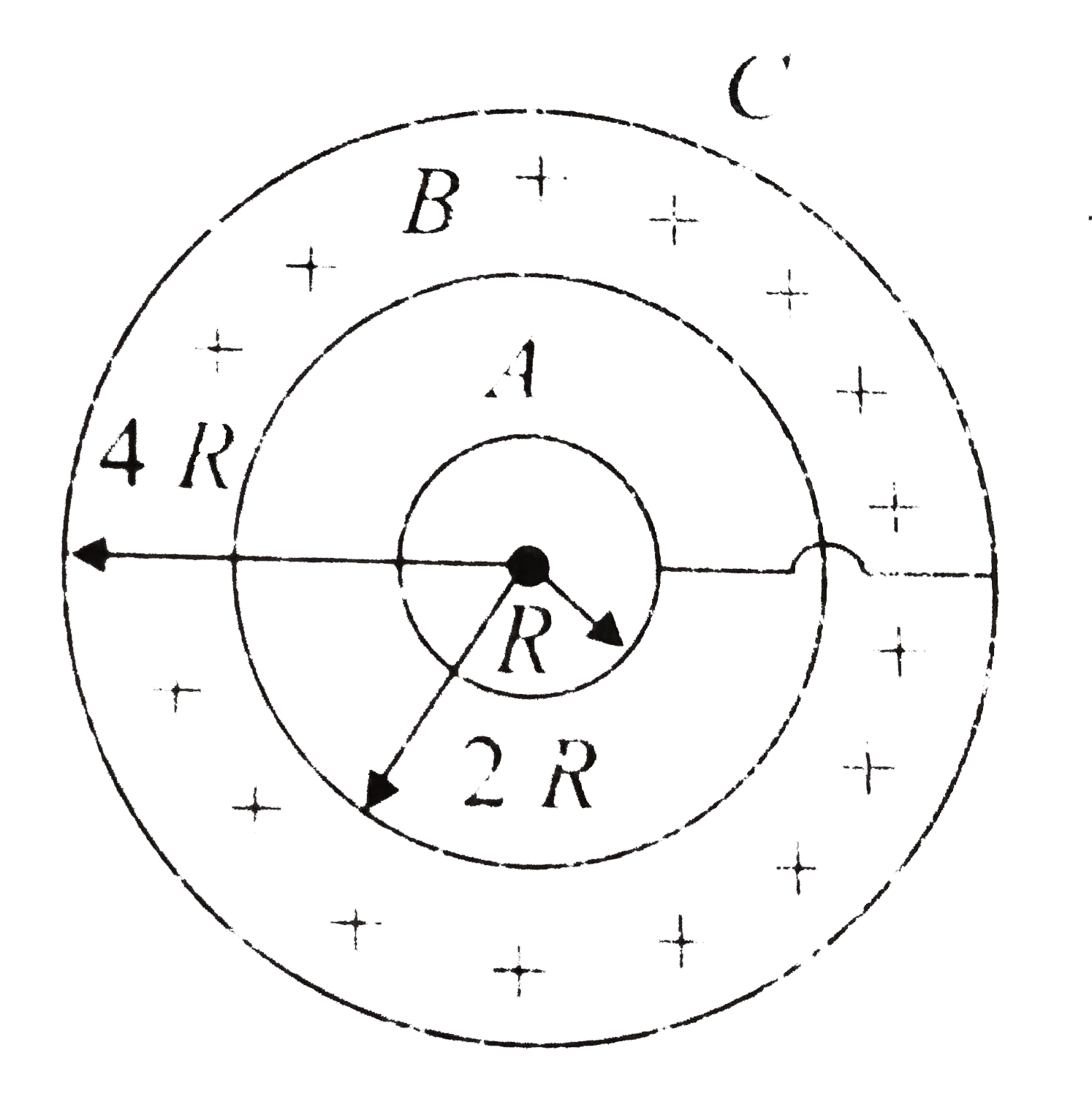
Potential at A isView SolutionFigure shows a system of three concentric metal shells, A, B and C with radii a, 2a and 3a respectively. Shell B is earthed and shell C is given a charge Q. Now if shell C is connected to shell A, then find the final charge on the shell B
 View Solution
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionTwo concentric spherical conducting shells of radii 'a' and 2a are initially given charges +2Q and +Q respectively as shown. The total heat dissipated after switch 'S' has been closed is (where k=14πε0)
 View Solution
View SolutionThere are two concentric conducting spherical shells of radius rA and rB respectively (rB=2rA). If the inner shell is given a charge Q and outer shell is given a charge 2Q, then the potential difference between the surfaces of the shells will be K=14πε0
View Solution

