Distance of propogation from antenna of height 20m is
80km
8km
16km
6.8km
The correct Answer is:C
To find the distance of propagation from an antenna of height 20 meters, we can use the formula for the range of an antenna:
1. Identify the Formula:
The distance of propagation (or range) from an antenna can be calculated using the formula:
d=√2⋅re⋅ht
where:
- d is the distance of propagation,
- re is the radius of the Earth (approximately 6.4×106 meters),
- ht is the height of the antenna.
2. Substitute the Known Values:
Given:
- Height of the antenna, ht=20 meters,
- Radius of the Earth, re=6.4×106 meters.
Substitute these values into the formula:
d=√2⋅(6.4×106)⋅20
3. Calculate the Product Inside the Square Root:
First, calculate 2⋅6.4×106:
2⋅6.4×106=12.8×106
Now multiply by the height of the antenna:
12.8×106⋅20=256×106
4. Take the Square Root:
Now, we take the square root of 256×106:
d=√256×106=√256⋅√106=16⋅103=16000 meters
5. Convert to Kilometers:
Since 1 kilometer=1000 meters:
d=160001000=16 kilometers
Final Answer:
The distance of propagation from the antenna of height 20 meters is 16 kilometers.
---
The distance of propagation (or range) from an antenna can be calculated using the formula:
d=√2⋅re⋅ht
where:
- d is the distance of propagation,
- re is the radius of the Earth (approximately 6.4×106 meters),
- ht is the height of the antenna.
Given:
- Height of the antenna, ht=20 meters,
- Radius of the Earth, re=6.4×106 meters.
d=√2⋅(6.4×106)⋅20
First, calculate 2⋅6.4×106:
2⋅6.4×106=12.8×106
Now multiply by the height of the antenna:
12.8×106⋅20=256×106
Now, we take the square root of 256×106:
d=√256×106=√256⋅√106=16⋅103=16000 meters
Since 1 kilometer=1000 meters:
d=160001000=16 kilometers
The distance of propagation from the antenna of height 20 meters is 16 kilometers.
Similar Questions
Knowledge Check
The maximum line-of -sight distance dM between two antennas having heights hT and HR above the earth is
A√R(hT+hR)B√2R/(hT+hR)C√RhT+√2RhRD√2RhT+√2RhRThe maximum line-of -sight distance dM between two antennas having heights hT and HR above the earth is
A√R(hT+hR)B√2R/(hT+hR)C√RhT+√2RhRD√2RhT+√2RhR
Two particle of equal mass are projected simultaneously from the roof of a tower of height 20 m with same speed 20m//s, one horizontally and the other vertically upwards. Choose the correct alternative (s).
View SolutionJai is standing on the top of a building of height 25 m he wants to throw his gun to Veeru who stands on top of another building of height 20 m at distance 15 m from first building. For which horizontal speed of projectile, it is possible?
View Solution5 m high pole stands on a building of height 25 m. The pole and the building subtend equal angles at an antenna placed at a height of 30 m. The distanceo f the antenna from the top of the pole is
View SolutionIn figure , the angle of elevation of the top of a tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m, Find the distance of the point from the foot of the power .
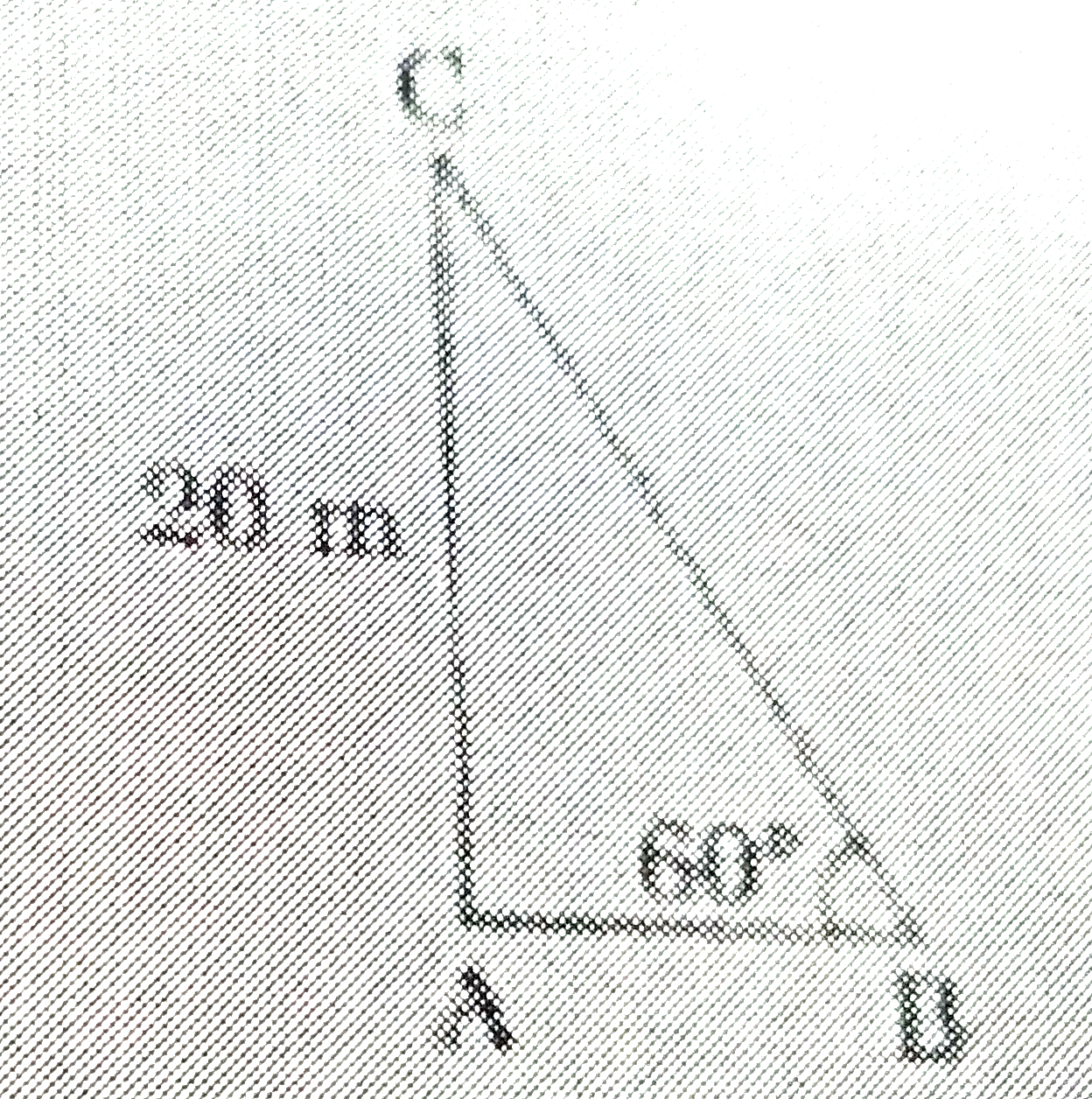
View SolutionA slightly divergent beam of charged particles accelerated by a Potential difference V propogates from a point A along the axis of a solenoid. The beam is brought into focus at a distance l from the point A at two successive values of magnetic induction B1andB2. Find the specific charge q/m of the particles.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View Solution
