Jai is standing on the top of a building of height 25 m he wants to throw his gun to Veeru who stands on top of another building of height 20 m at distance 15 m from first building. For which horizontal speed of projectile, it is possible?
5ms−1
10ms−1
15ms−1
20ms−1
The correct Answer is:C
To solve the problem step by step, we need to analyze the motion of the projectile (the gun) that Jai throws from the top of a building to Veeru on another building.
Step 1: Understand the vertical and horizontal distances
- Jai is on a building of height 25 m.
- Veeru is on a building of height 20 m.
- The vertical distance the gun needs to fall is:
Vertical distance=25m−20m=5m
- The horizontal distance between the two buildings is 15 m.
Step 2: Use the equations of motion for vertical motion
- The vertical motion can be described by the second equation of motion:
s=ut+12gt2
where:
- s is the vertical distance (5 m),
- u is the initial vertical velocity (0 m/s, since it is thrown horizontally),
- g is the acceleration due to gravity (approximately 9.81m/s2),
- t is the time in seconds.
Substituting the known values into the equation:
5=0⋅t+12⋅9.81⋅t2
This simplifies to:
5=12⋅9.81⋅t2
5=4.905⋅t2
Step 3: Solve for time t
Rearranging the equation to solve for t2:
t2=54.905
Calculating t2:
t2≈1.0204
Taking the square root to find t:
t≈1.01s(approximately 1s)
Step 4: Use the horizontal motion to find the required speed
- The horizontal motion can be described by the equation:
x=ut
where:
- x is the horizontal distance (15 m),
- u is the horizontal speed (what we need to find),
- t is the time (approximately 1 s).
Substituting the known values:
15=u⋅1
Thus, solving for u:
u=15m/s
Final Answer
The horizontal speed of the projectile required for Jai to successfully throw the gun to Veeru is 15 m/s.
---
- Jai is on a building of height 25 m.
- Veeru is on a building of height 20 m.
- The vertical distance the gun needs to fall is:
Vertical distance=25m−20m=5m
- The horizontal distance between the two buildings is 15 m.
- The vertical motion can be described by the second equation of motion:
s=ut+12gt2
where:
- s is the vertical distance (5 m),
- u is the initial vertical velocity (0 m/s, since it is thrown horizontally),
- g is the acceleration due to gravity (approximately 9.81m/s2),
- t is the time in seconds.
5=0⋅t+12⋅9.81⋅t2
This simplifies to:
5=12⋅9.81⋅t2
5=4.905⋅t2
Rearranging the equation to solve for t2:
t2=54.905
Calculating t2:
t2≈1.0204
Taking the square root to find t:
t≈1.01s(approximately 1s)
- The horizontal motion can be described by the equation:
x=ut
where:
- x is the horizontal distance (15 m),
- u is the horizontal speed (what we need to find),
- t is the time (approximately 1 s).
15=u⋅1
Thus, solving for u:
u=15m/s
The horizontal speed of the projectile required for Jai to successfully throw the gun to Veeru is 15 m/s.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type26videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type35videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
Similar Questions
A chimeny of 20 m height standing on the top of a building subtends an angle whose tangent is 16 at a distance of 70 m from the foot of the building, then the height of building is
View SolutionA ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
View Solution5 m high pole stands on a building of height 25 m. The pole and the building subtend equal angles at an antenna placed at a height of 30 m. The distanceo f the antenna from the top of the pole is
View SolutionFrom the top of a building 60m high the angles of depression of the top and the bottom of a tower are observed to be 30o and 60o . Find the height of the tower.
View SolutionA statue of height 4 m stands on a tower of height 10 m. The angle subtended by the status at the eyes of an observer of height 2m, standing at a distance of 6m from base of the tower is
View SolutionA ladder 17m long reaches a window of a building 15m above the ground. Find the distance of the foot of the ladder from the building.
View SolutionThe angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
View SolutionFigure shows a projectile thrown with speed u = 20 m/s at an angle 30∘ with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is
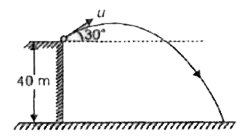 View Solution
View SolutionA ladder, 25 m long reaches a window of building 20 m, above the ground. The distance of the foot of the ladder from the building.
View SolutionA person standing at point P sees angle of elevation of the top of a building, whose base is 50 meters away, to be 60∘. Another building whose base is 20 meters away from the base of the first building and is between the observer and first building has height h meters, then the maximum possible height (in meters) of this second building is (Take √3=1.73)
View Solution

