A step index fibre has a relative refractive index difference of 0.86% Estimate the critical angle at the core-cladding interface
The correct Answer is:82.4∘
To estimate the critical angle at the core-cladding interface of a step index fiber with a relative refractive index difference of 0.86%, we can follow these steps:
1. Understanding the Concept of Critical Angle:
The critical angle (θc) is defined as the angle of incidence above which total internal reflection occurs. It can be calculated using the formula:
sin(θc)=μrμd
where μr is the refractive index of the cladding and μd is the refractive index of the core.
2. Relative Refractive Index Difference:
The relative refractive index difference (Δ) is given as 0.86%. This can be expressed as:
Δ=μd−μrμd×100
Rearranging this gives:
μd−μrμd=0.86100=0.0086
3. Expressing μr in terms of μd:
From the rearranged equation, we can express μr as:
μr=μd×(1−0.0086)=μd×0.9914
4. Substituting μr into the Critical Angle Formula:
Now we can substitute μr into the critical angle formula:
sin(θc)=μrμd=μd×0.9914μd=0.9914
5. Calculating the Critical Angle:
Now, we can find the critical angle by taking the inverse sine:
θc=sin−1(0.9914)
Using a calculator, we find:
θc≈82.48∘
Final Answer:
The critical angle at the core-cladding interface is approximately 82.48∘.
---
The critical angle (θc) is defined as the angle of incidence above which total internal reflection occurs. It can be calculated using the formula:
sin(θc)=μrμd
where μr is the refractive index of the cladding and μd is the refractive index of the core.
The relative refractive index difference (Δ) is given as 0.86%. This can be expressed as:
Δ=μd−μrμd×100
Rearranging this gives:
μd−μrμd=0.86100=0.0086
From the rearranged equation, we can express μr as:
μr=μd×(1−0.0086)=μd×0.9914
Now we can substitute μr into the critical angle formula:
sin(θc)=μrμd=μd×0.9914μd=0.9914
Now, we can find the critical angle by taking the inverse sine:
θc=sin−1(0.9914)
Using a calculator, we find:
θc≈82.48∘
The critical angle at the core-cladding interface is approximately 82.48∘.
Similar Questions
A step index fibre has a relative refractive index difference of 0.9%.Estimate the critical angle at the core -cladding interface,when the core index is 1.46.find the numerical aperture,if the source to fiber medium is air.
View SolutionA sept index fibre has a relavitive refractive index of 0.88%. What is the critical angle at the core-cladding interface?
View SolutionA silicon optical fibre with a core diameter large enough has a core refractive index of 1.50 and a cladding refrcative index 1.47.Determine(i)the critical angle at the core cladding interface.(ii)the numerical aperture for the fibre.(iii)the acceptance angle in air for the fibre.
View SolutionIn opticle fibres,the refractive index of the core is
View SolutionHow is the critical angle related to the refractive index of a medium ?
View SolutionThe velocity of light in the core of a step index fibre 2×108m/s and the critical angle at the core-cladding interface is 80∘.Find the numerical aperture and the acceptance angle for the fibre in air.The velocity of light in vacuum is 3×108m/s
View SolutionA ray of light travelling in glass having refractive index _(a)μg=3/2 is incident at a critical angle C on the glass air interface. If a thin layer of water is poured on glass air interface, then what will be the angle of emergence of this ray in air when it emerges from water air inteface?
View Solution(i) What is the relation between critical angle and refractive index of a material ?
(ii) Does critical angle depend on the color of light ? Explain.
View SolutionState the relation between the critical angle and the absolute refractive index of a medium.
View SolutionIn the diagram shown, light is incident on the interface between media 1 (refractive index n1) and 2 (refractive index n2) at angle slightly greater than the critical angle, and is totally reflected. The light is then also totally reflected at the interface between media 1 and 3 (refractive index n3), after which it travels in a direction opposite to its initial direction, The media must have a refractive indices such that.
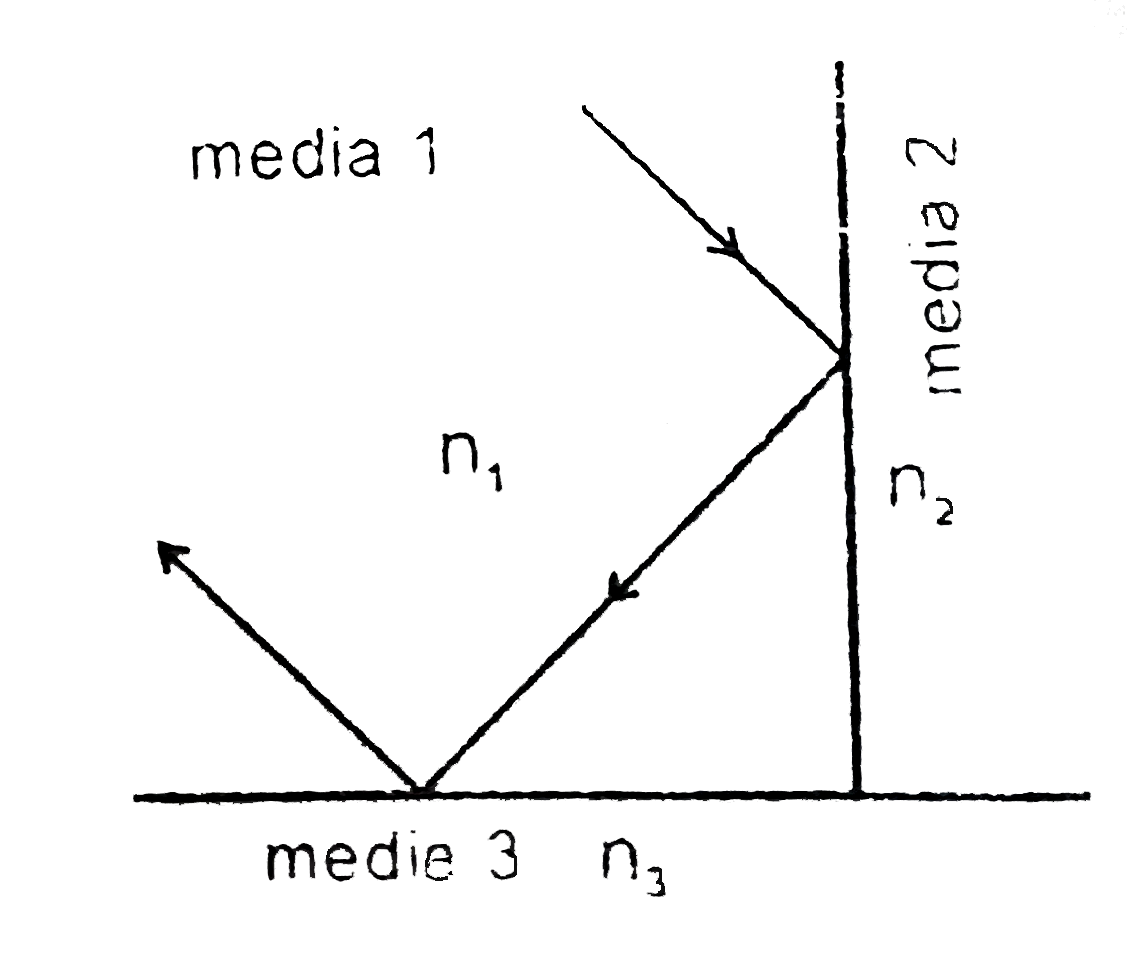 .
.
View Solution
