Find the excitation energy of n = 3 level of He atom
48.4 eV
2.4 eV
3.8 eV
24.2 eV
The correct Answer is:A
To find the excitation energy of the n = 3 level of the helium atom, we will follow these steps:
Step 1: Understand the Concept of Excitation Energy
Excitation energy is the energy required to move an electron from a lower energy level (ground state) to a higher energy level. For the helium atom, we will consider the transition from the ground state (n = 1) to the excited state (n = 3).
Step 2: Write the Formula for Energy Levels
The energy of an electron in a hydrogen-like atom is given by the formula:
En=−13.6eV⋅Z2n2
where:
- En is the energy of the level,
- Z is the atomic number (for helium, Z=2),
- n is the principal quantum number.
Step 3: Calculate the Energy for n = 1 and n = 3
1. For n = 1 (Ground State):
E1=−13.6eV⋅2212=−13.6⋅41=−54.4eV
2. For n = 3 (Excited State):
E3=−13.6eV⋅2232=−13.6⋅49=−6.04eV
Step 4: Calculate the Excitation Energy
The excitation energy (EEX) required to move from the ground state to the excited state is given by:
EEX=E3−E1
Substituting the values we calculated:
EEX=(−6.04eV)−(−54.4eV)=−6.04+54.4=48.36eV
Step 5: Final Result
Thus, the excitation energy of the n = 3 level of the helium atom is approximately:
EEX≈48.4eV
Excitation energy is the energy required to move an electron from a lower energy level (ground state) to a higher energy level. For the helium atom, we will consider the transition from the ground state (n = 1) to the excited state (n = 3).
The energy of an electron in a hydrogen-like atom is given by the formula:
En=−13.6eV⋅Z2n2
where:
- En is the energy of the level,
- Z is the atomic number (for helium, Z=2),
- n is the principal quantum number.
1. For n = 1 (Ground State):
E1=−13.6eV⋅2212=−13.6⋅41=−54.4eV
E3=−13.6eV⋅2232=−13.6⋅49=−6.04eV
The excitation energy (EEX) required to move from the ground state to the excited state is given by:
EEX=E3−E1
Substituting the values we calculated:
EEX=(−6.04eV)−(−54.4eV)=−6.04+54.4=48.36eV
Thus, the excitation energy of the n = 3 level of the helium atom is approximately:
EEX≈48.4eV
Similar Questions
If the first excitation energy of a hydrogen - like atom is 27.3 eV , then ionization energy of this atom will be
View SolutionStatement-1 : The excitation energy of He+ in its first excited state is 4 times the excitation energy of H in its first excited state.
Statement-2 : The whose energies are defined by the expansion E=−E0Z2n2 are stable, where Z and n are atomic number of the atom and principal quantum number of the orbit, respectively.
View SolutionThe first excitation potential of a hypothetical hydrogen- like atom is 15V. Find the third excitation potential of the atom.
View SolutionIn a mixture of H−He+ gas (He+is singly ionized He atom), H atom and He+ ions are excited to their respective first excited state. Subsequently H atoms transfer their total excitation energy to He+ ions (by collisions) Assume that the bohr model of atom is exactly valid.
The ratio of the kinetic energy of the n=2 electron for the H atom to the of He+ lon is -
View SolutionA gas of identical hydrogen-like atoms has some atoms in the lowest in lower (ground) energy level A and some atoms in a partical upper (excited) energy level B and there are no atoms in any other energy level.The atoms of the gas make transition to higher energy level by absorbing monochromatic light of photon energy 2.7eV.
Subsequenty , the atom emit radiation of only six different photon energies. Some of the emitted photons have energy 2.7eV some have energy more , and some have less than 2.7eV.
a Find the principal quantum number of the intially excited level B
b Find the ionization energy for the gas atoms.
c Find the maximum and the minimum energies of the emitted photons.
View SolutionIn a mixture of He⊕ gas H atom and He⊕ ions Are excited to three respective first excited subsepuenly , H atom transfers its total excitation energy to He⊕ions by collision .Assuming that Bohr model of an atom is applicable , answer the following question
The ratio of teh potential energy of the n=2 electron for H atom to the of He⊕ ion is
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
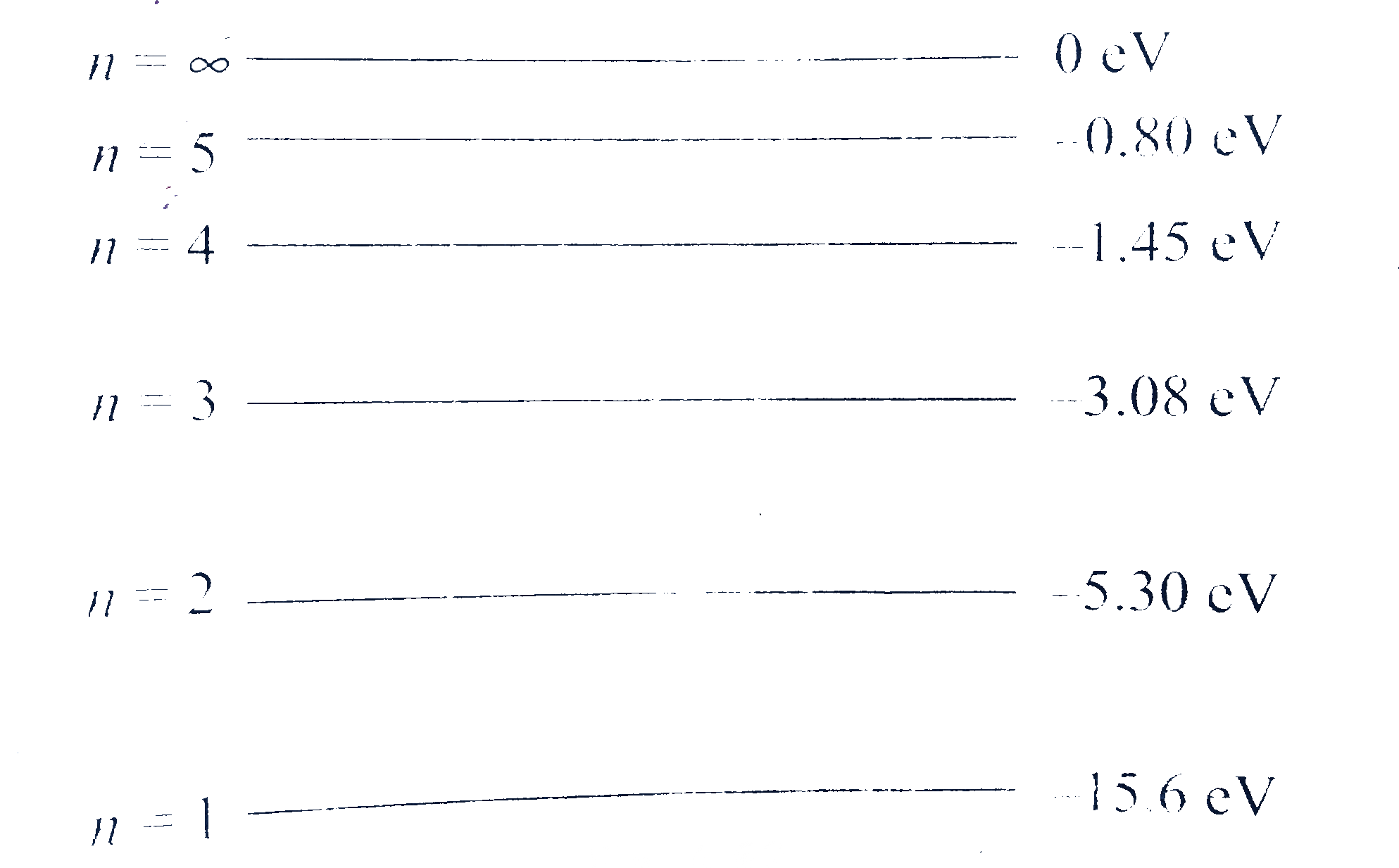
Find the excitation potential for the state n=3.
View SolutionIn a mixture of H−He+ gas (He+ is singly ionized He atom), H atoms and He+ ions are excited to their respective first excited states. Subsequently, H atoms transfer their total excitation energy to He+ ions (by collisions). Assume that the Bohr model of atom is exctly valid.
The ratio of the kinetic energy of the n=2 electron for the H atom to that of He+ ion is:
View SolutionFind the radius and energy of He+ ion in the states (a) n=2,(b)n=3
View SolutionAn electron is excited to fourth energy level in an atom. It will
View Solution
