A particle is moving in such a way that at one instant velocity vector of the particle is 3ˆi+4ˆjm/s and acceleration vector is −25ˆi−25ˆjm/s? The radius of curvature of the trajectory of the particle at that instant is
2 m
3 m
5 m
10 m
The correct Answer is:C
To find the radius of curvature of the trajectory of the particle, we can use the formula:
R=V2A⊥
where:
- R is the radius of curvature,
- V is the magnitude of the velocity,
- A⊥ is the perpendicular component of the acceleration.
Step 1: Calculate the magnitude of the velocity vector
The velocity vector is given as:
→V=3^i+4^j
The magnitude of the velocity V can be calculated using the formula:
V=√V2x+V2y=√32+42=√9+16=√25=5m/s
Step 2: Calculate the magnitude of the acceleration vector
The acceleration vector is given as:
→A=−25^i−25^j
The magnitude of the acceleration A can be calculated as:
A=√A2x+A2y=√(−25)2+(−25)2=√625+625=√1250=25√2m/s2
Step 3: Find the angle between the velocity and acceleration vectors
To find the angle θ between the velocity and acceleration vectors, we can use the dot product:
→V⋅→A=|→V||→A|cos(θ)
Calculating the dot product:
→V⋅→A=(3)(−25)+(4)(−25)=−75−100=−175
Now substituting the magnitudes:
−175=(5)(25√2)cos(θ)
Solving for cos(θ):
cos(θ)=−175125√2=−75√2
Step 4: Calculate the perpendicular component of acceleration
The perpendicular component of acceleration A⊥ can be found using:
A⊥=Asin(θ)
Using the identity sin2(θ)+cos2(θ)=1:
sin2(θ)=1−(−75√2)2=1−4950=150
Thus,
sin(θ)=1√50=15√2
Now substituting back to find A⊥:
A⊥=Asin(θ)=25√2⋅15√2=5m/s2
Step 5: Calculate the radius of curvature
Now we can substitute V and A⊥ into the radius of curvature formula:
R=V2A⊥=525=255=5m
Final Answer
The radius of curvature of the trajectory of the particle at that instant is 5m.
- R is the radius of curvature,
- V is the magnitude of the velocity,
- A⊥ is the perpendicular component of the acceleration.
The velocity vector is given as:
The acceleration vector is given as:
To find the angle θ between the velocity and acceleration vectors, we can use the dot product:
The perpendicular component of acceleration A⊥ can be found using:
Now we can substitute V and A⊥ into the radius of curvature formula:
The radius of curvature of the trajectory of the particle at that instant is 5m.
Similar Questions
A particle is moving in x-y plane. At an instant, it has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2 At that instant, the radius of curvature of its path will be :
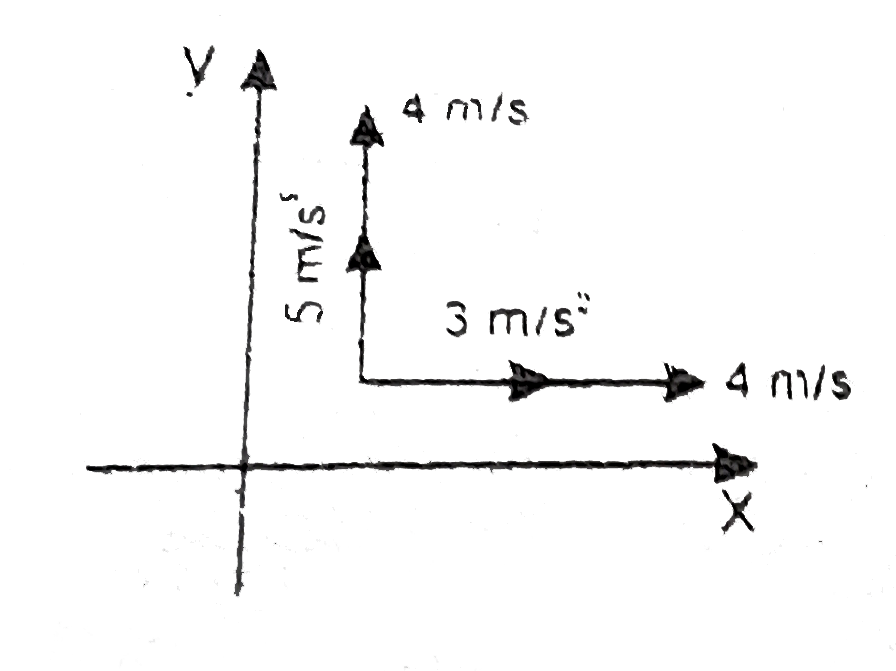
View SolutionInitial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle :
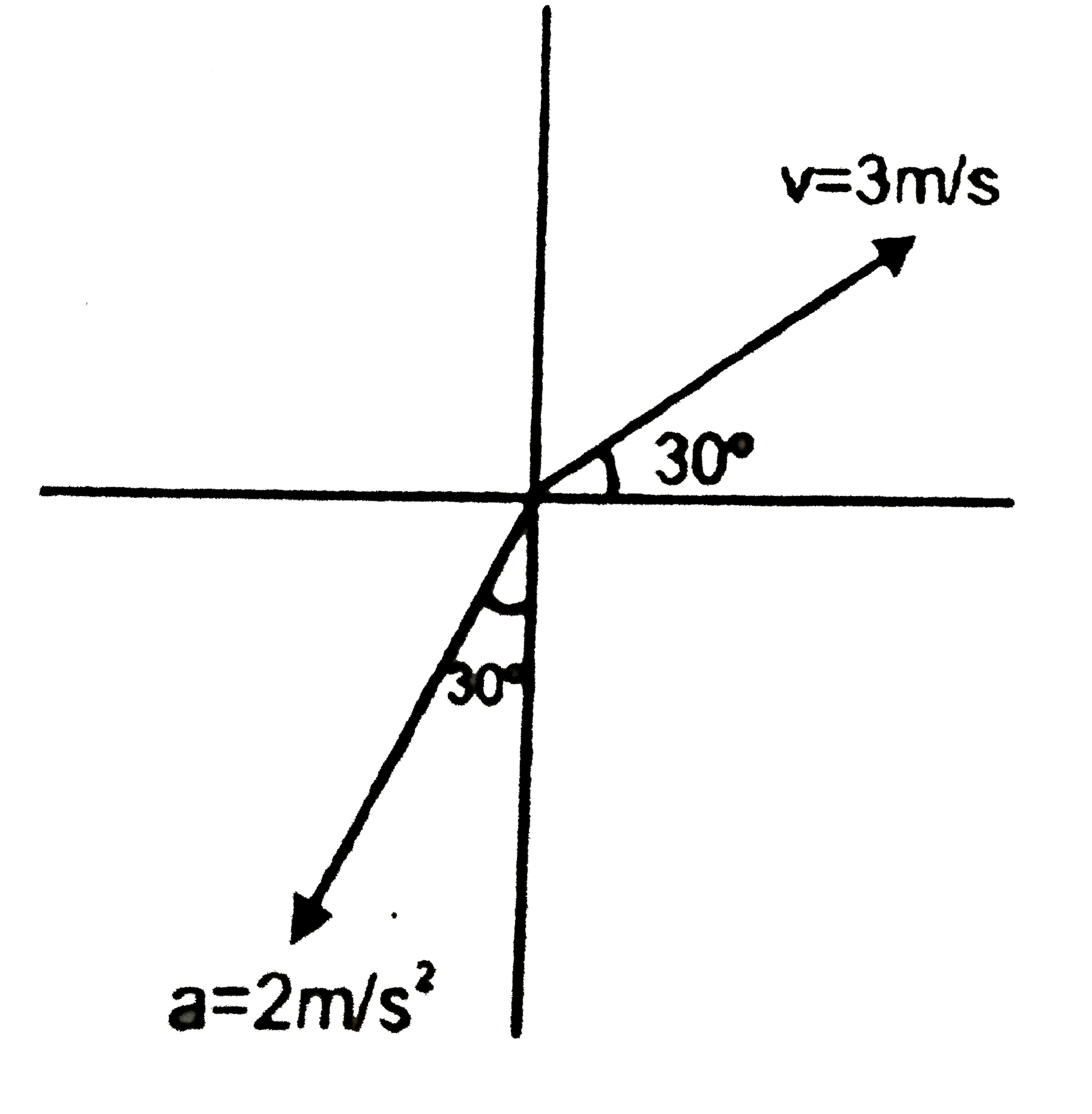
View Solution
Knowledge Check
A particle starts from origin at t=0 with a constant velocity 5ˆim/s and moves in x−y plane under action of a force which produce a constant acceleration of (3ˆi+2ˆj)m/s2 the y-coordinate of the particle at the instant its x co-ordinate is 84m in m is
A12 mB24 mC36 mD48 m
A particle starts from origin at t=0 with a constant velocity 5ˆjm/s and moves in x−y plane under action of a force which produce a constant acceleration of (3ˆi+2ˆj)m/s2 the y-coordinate of the particle at the instant its x co-ordinate is 24m in m is
View SolutionA particle is moving in x-y plane. Its initial velocity and acceleration are u=(4ˆi+8ˆj)m/sanda=(2ˆi−4ˆj)m/s2. Find
(a) the time when the particle will cross the x-axis.
(b) x-coordinate of particle at this instant.
(c) velocity of the particle at this instant.
Initial coordinates of particle are (4m,10m).
View SolutionA small object of mass of 100 g moves in a circular path . At a given instant velocity of the object is 10ˆims−1 and acceleration is (20ˆi+10ˆj)ms−2. At this instant of time. the rate of change of kinetic energy of the object is
View SolutionA particle is moving with a constant acceleration →a=ˆi−2ˆj+2ˆkm/s2 and instantaneous velocity →v=ˆi+2ˆj+2ˆkm/s, then rate of change of speed of particle 2 second after this instant will be :
View SolutionA particle has an initial velocity of 4ˆi+3ˆj and an acceleration of 0.4ˆi+0.3ˆj. Its speed after 10s is
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle of position vector (3ˆi+2ˆj+ˆk). Calculate the torque acting on the particle.
View SolutionA particle starts from the origin at t = 0 s with a velocity of 10.0ˆj m/s and moves in plane with a constant acceleration of (8ˆi+2ˆj)ms−2. The y-coordinate of the particle in 2 sec is
View Solution
