The velocity of a particle moving in a straight line is decreasing at the rate of 3m/s per metre of displacement at an instant when the velocity is 10m/s. Determine the acceleration of the particle at this instant.
The correct Answer is:B, C
dvds=−3m/sm
a=v.dvds
=(10)(−3)
=−30m/s2
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Objective45videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
If the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionInstantaneous velocity of a particle moving in astraight line is given as v=(4+4√t)m/s. For the first five second of motion. Then after velocity of it becomes a constant. Find the acceleration of the particle at time t = 3.0 s and its displacement till this instant.
View Solution
Knowledge Check
- Question 1 - Select One
If the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
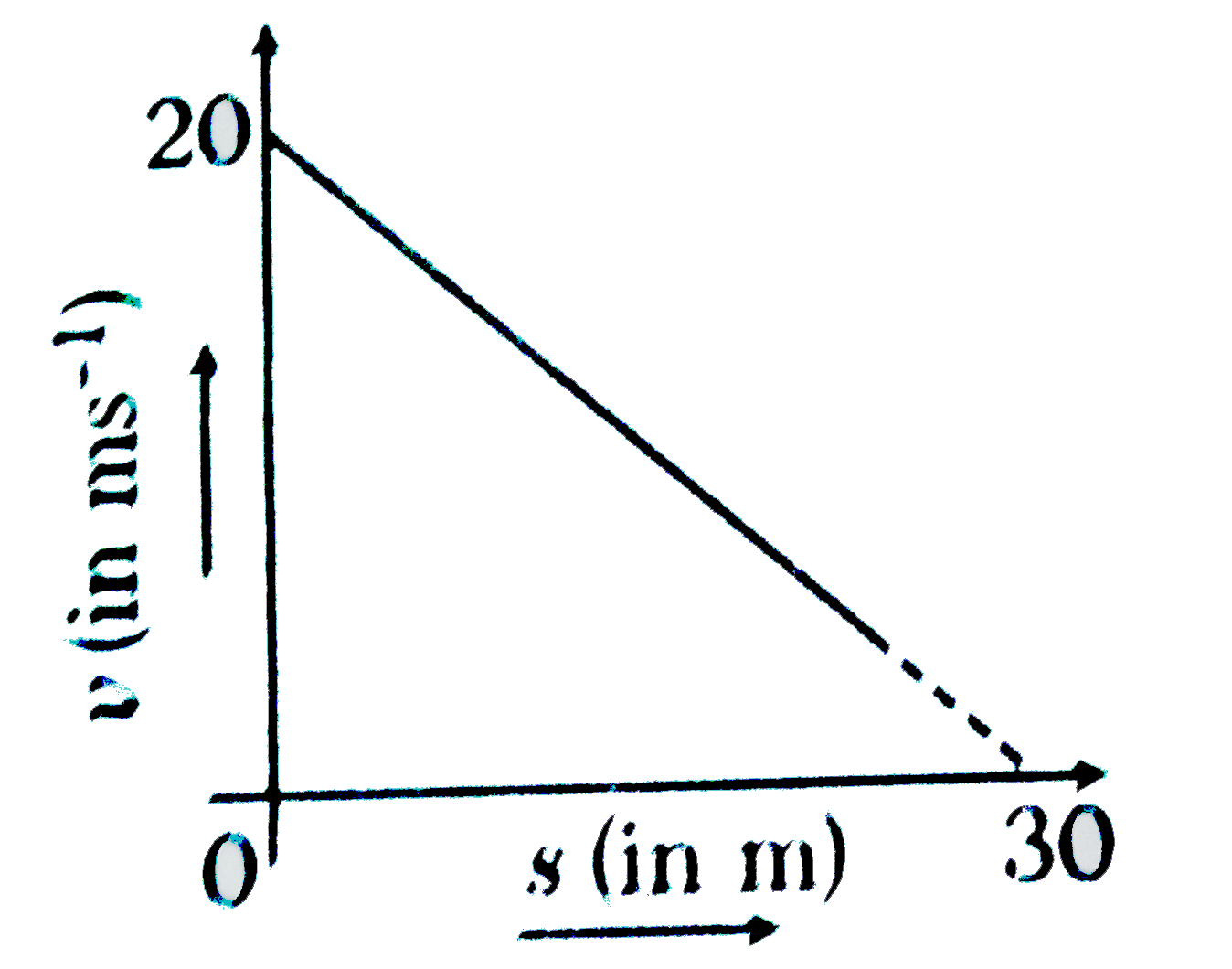 A23ms−2B−23ms−2C203ms−2D−203ms−2
A23ms−2B−23ms−2C203ms−2D−203ms−2 - Question 2 - Select One
The velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :
 A23ms−2B−23ms−2C203ms−2D−203ms−2
A23ms−2B−23ms−2C203ms−2D−203ms−2 - Question 3 - Select One
For a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
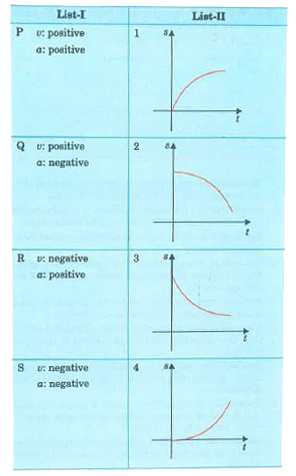 APQRS3241BPQRS1324CPQRS2134DPQRS4132
APQRS3241BPQRS1324CPQRS2134DPQRS4132
For a particle moving along a straight line, the relation between the velocity and the displacement at any instant is given by v2=S2+2S2+3
Find the acceleration of the particle when it is at a distance of 4 meters from a fixed point on the line.View SolutionVelocity versus displacement curve of a particle moving in straight line is shown in the figure from a point P, a line is drawn perpendicular to displacement axis and line PR is drawn normal to the curve at P. The instantaneous acceleration of the particle at point P is V(m/s) (2,0) R (3,0) S(m)
View SolutionVelocity of a particle at some instant is v=(3ˆi+4ˆj+5ˆk)m/s. Find speed of the particle at this instant.
View SolutionA particle is moving along a straight line with constant acceleration. At the end of tenth second its velocity becomes 20m/s and in tenth second it travels a distance of 10m. Then the acceleration of the particle will be.
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?View Solution

