A stone is projected at time t=0 with a speed v0 at an angle θ with the horizontal in a uniform gravitational field. The rate of work done (P) by the gravitational force plotted against time (t) will be as.

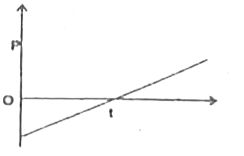
The correct Answer is:D
To solve the problem, we need to analyze the work done by the gravitational force on the stone projected at an angle. The work done by a force is given by the formula:
P=F⋅v
where P is the power (rate of work done), F is the force, and v is the velocity of the object.
1. Identify the Forces:
The gravitational force acting on the stone is given by:
F=−mg^j
where m is the mass of the stone, g is the acceleration due to gravity, and ^j is the unit vector in the vertical direction (downward).
2. Determine the Velocity Components:
The stone is projected with an initial speed v0 at an angle θ. The velocity components can be expressed as:
Vx=v0cos(θ)andVy=v0sin(θ)−gt
Here, Vy decreases over time due to the gravitational acceleration g.
3. Calculate the Dot Product:
The power can be expressed as:
P=F⋅v=(−mg^j)⋅(Vx^i+Vy^j)=−mgVy
Substituting for Vy:
P=−mg(v0sin(θ)−gt)
This simplifies to:
P=−mgv0sin(θ)+mg2t
4. Analyze the Expression:
The expression for power P can be rearranged as:
P=mg2t−mgv0sin(θ)
This is a linear equation in terms of time t with:
- A slope of mg2
- A y-intercept of −mgv0sin(θ)
5. Conclusion:
Since the equation is linear, the graph of power P against time t will be a straight line with a positive slope, indicating that the rate of work done by the gravitational force increases linearly with time.
Final Answer:
The rate of work done (P) by the gravitational force plotted against time (t) will be a straight line with a positive slope.
The gravitational force acting on the stone is given by:
F=−mg^j
where m is the mass of the stone, g is the acceleration due to gravity, and ^j is the unit vector in the vertical direction (downward).
The stone is projected with an initial speed v0 at an angle θ. The velocity components can be expressed as:
Vx=v0cos(θ)andVy=v0sin(θ)−gt
Here, Vy decreases over time due to the gravitational acceleration g.
The power can be expressed as:
P=F⋅v=(−mg^j)⋅(Vx^i+Vy^j)=−mgVy
Substituting for Vy:
P=−mg(v0sin(θ)−gt)
This simplifies to:
P=−mgv0sin(θ)+mg2t
The expression for power P can be rearranged as:
P=mg2t−mgv0sin(θ)
This is a linear equation in terms of time t with:
- A slope of mg2
- A y-intercept of −mgv0sin(θ)
Since the equation is linear, the graph of power P against time t will be a straight line with a positive slope, indicating that the rate of work done by the gravitational force increases linearly with time.
The rate of work done (P) by the gravitational force plotted against time (t) will be a straight line with a positive slope.
Similar Questions
A heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA bode mass m is projected at an angle θ with the horizontal with an initial velocity u, the average power of gravitational force over the whole time of flight is.
View SolutionThe figure shows the velocity (v) of a particle plotted against time (t).
 View Solution
View SolutionThe figure shows the velocity (v) of a particle plotted against time (t).
 View Solution
View SolutionA body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
View SolutionWhen a body is projected at an angle with the horizontal in the uniform gravitational field of the earth, the angular momentum of the body about the point of projection, as it proceeds along its path
View SolutionA particle is projected at time t=0 from a point P wilth a speed v0 at an angle of 45∘ to the horizontal. Find the magnitude and the direction of the angular momentum of the particle about the point P at time t=v0g
View SolutionA particle is projected at t=0 from a point on the ground with certain velocity at an angle with the horizontal. The power of gravitation force is plotted against time. Which of the following is the best representation?
View SolutionA particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
View Solution

