A particle is projected at t=0 from a point on the ground with certain velocity at an angle with the horizontal. The power of gravitation force is plotted against time. Which of the following is the best representation?
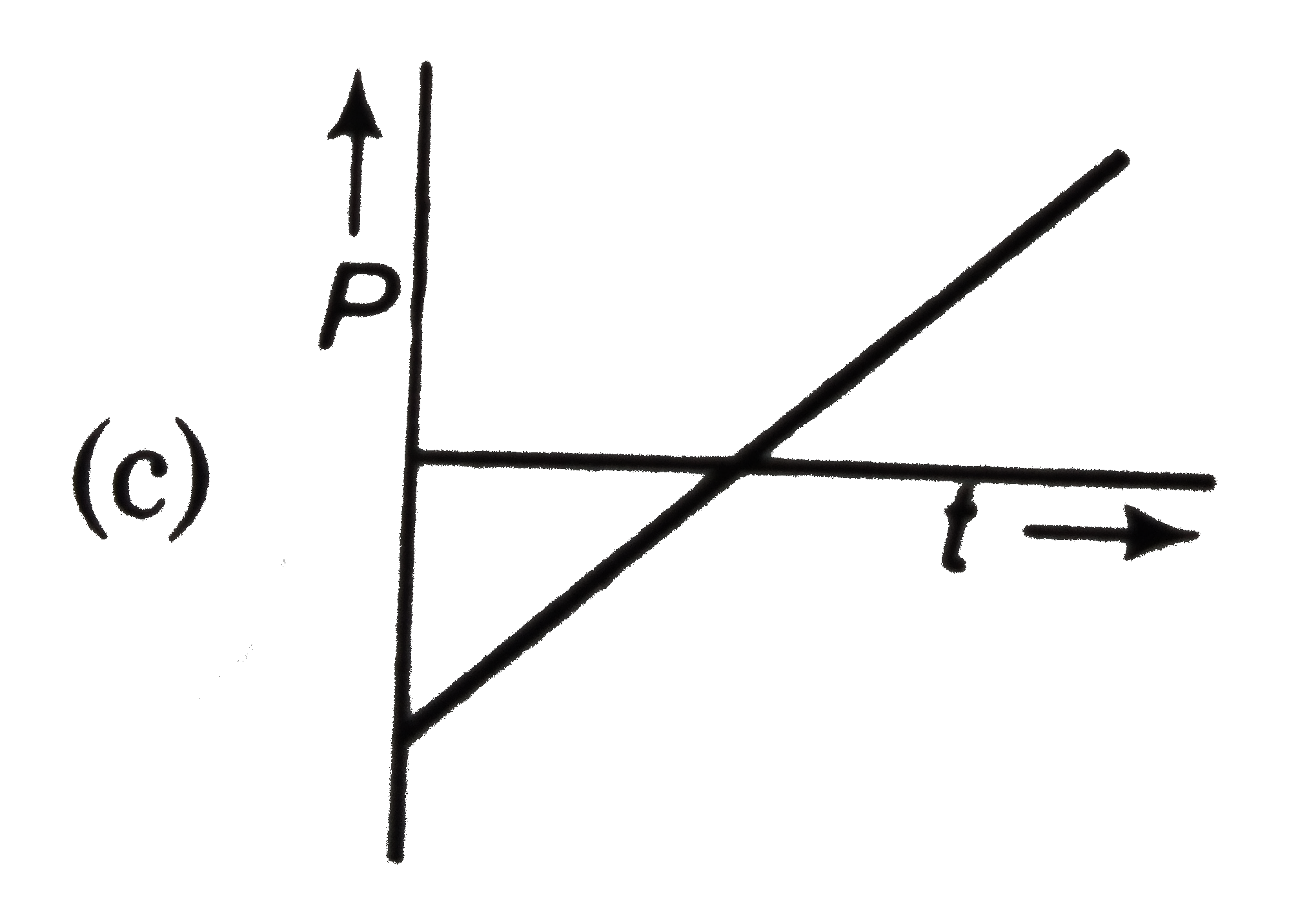
The correct Answer is:C
To solve the problem step by step, we need to analyze the power of the gravitational force acting on a particle projected at an angle. Here’s how we can break it down:
Step 1: Understand the scenario
A particle is projected from the ground at an angle θ with an initial velocity u. The motion of the particle will follow a projectile path under the influence of gravity.
Step 2: Resolve the initial velocity
The initial velocity can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
Step 3: Identify the force acting on the particle
The only force acting on the particle after projection is the gravitational force, which is directed downward:
- Gravitational force, Fg=−mg^j
Step 4: Write the velocity vector at any time t
At any time t, the velocity vector →v can be expressed as:
→v=ucosθ^i+(usinθ−gt)^j
Here, −gt accounts for the downward acceleration due to gravity.
Step 5: Calculate the power at any instant
Power P is defined as the dot product of the force and velocity:
P=→F⋅→v
Substituting the values:
P=(−mg^j)⋅(ucosθ^i+(usinθ−gt)^j)
This simplifies to:
P=−mg(usinθ−gt)
Thus, we can express the power as:
P=−mgusinθ+mggt
Step 6: Analyze the power with respect to time
From the equation P=−mgusinθ+mggt, we see that:
- The term mggt indicates that power increases linearly with time.
- The initial power will be negative (when the particle is moving upwards against gravity) and will become positive after reaching the peak (when the particle starts moving downwards).
Step 7: Conclusion
The power of the gravitational force plotted against time will show a linear relationship. Initially, the power will be negative and will increase to positive as time progresses.
Final Representation
The best representation of the power of gravitational force against time is a linear graph that starts below the time axis (negative power) and crosses to above the time axis (positive power).
A particle is projected from the ground at an angle θ with an initial velocity u. The motion of the particle will follow a projectile path under the influence of gravity.
The initial velocity can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
The only force acting on the particle after projection is the gravitational force, which is directed downward:
- Gravitational force, Fg=−mg^j
At any time t, the velocity vector →v can be expressed as:
→v=ucosθ^i+(usinθ−gt)^j
Here, −gt accounts for the downward acceleration due to gravity.
Power P is defined as the dot product of the force and velocity:
P=→F⋅→v
Substituting the values:
P=(−mg^j)⋅(ucosθ^i+(usinθ−gt)^j)
This simplifies to:
P=−mg(usinθ−gt)
Thus, we can express the power as:
P=−mgusinθ+mggt
From the equation P=−mgusinθ+mggt, we see that:
- The term mggt indicates that power increases linearly with time.
- The initial power will be negative (when the particle is moving upwards against gravity) and will become positive after reaching the peak (when the particle starts moving downwards).
The power of the gravitational force plotted against time will show a linear relationship. Initially, the power will be negative and will increase to positive as time progresses.
The best representation of the power of gravitational force against time is a linear graph that starts below the time axis (negative power) and crosses to above the time axis (positive power).
Topper's Solved these Questions
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 More Than One Correct
Explore 9 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Subjective
Explore 15 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 1 subjective
Explore 27 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Integer Type Question
Explore 11 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
Knowledge Check
A particle is projected at time t=0 from a point P on the ground with a speed v0, at an angle of 45∘ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem t=v0/g
Aa. mv302√2gBb. mv30√2gCc. 3mv30√2gDd. √2mv30g
A particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.

View SolutionA heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
View SolutionA particle is projected from a horizontal floor with speed 10ms at an angle 30∘ with the floor and striking the floor after sometime. State which is correct.
View SolutionA particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
View SolutionA particle is projected with initaial velocity u at an angle 0 with horizontal, then variation of angular momentum L about starting w.r.t. Time t will be
View Solution
