The figure shows a model of perfume atomizer . When the bulb A is compressed , air (density ρa) flows through the vertical tube and emerges through the end . If excess pressure applied to the bulb ins progress be Δpthen the minimu speed of air in the tube to lift perfume is :
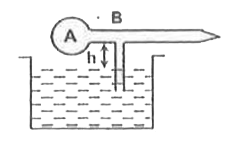
√2[Δp+ogh]ρa
√2[Δp−ρgh]ρa
√Δρ+ρghρa
None of these
Applying Bernoull.s principle at 1 and 2 , we obtain
P1+12ρav21=P2+12ρav22
Putting v1=0 since of the air is at rest inside the bulb ,
P1=P10+ΔPrP2=P0−ρgh whre ρ= density of liquid ( perfume)
ρa density of air
va = minimum velocity of air to lift the liquid through the height h = v (say)
P0 = atmospheric pressure
Hence ( A) is correct
Similar Questions
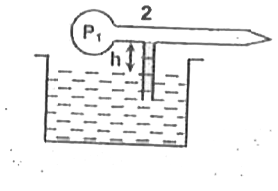
The figure shows a crude type of perfume atomizer. When bulb at A is compressed, air flows swifty through the tiny BC with uniform speed v, there by causing a reduced pressure at the position of verticall tube DE. The liquid of density 500kg/m3, then rises in the tube, enters tube BC and sprayed out. When bulb is in natural position the air in the bulb and tube are at atmospheric pressure P50=15N/m2. When bulb A is compressed, it creates an exces pressure Δp=0.001P0 inside the bulb A. Density of air is 1.3kg/m3. If the magnitude of minimum value of speed v required to cause the liquid to rise to tube BC is 5km/s. Find the value of k. (g=10m/s2)
View SolutionWater is flowing through a tube of radius r with a speed v. If this tube is joined to another tube of radius r/2, what is the speed of water in the second tube?
View SolutionWater is flowing through a long horizontal tube. Let PAandPB be the pressures at two points A and B of the tube
View SolutionFigure shows a crude type of atomizer. is compressed, air flows swiftly through tube BC causing a reduced pressure in the particles of the vertical to Liquid rises in the tube, enters BC and is sprayed out. if the pressure in the bulb is Pa+P, where P is the gauge pressure and Pa is the atmospheric pressure, v is the speed of air in BC, find how large would v need to be to cause the liquid to rise to BC. Density of air =1.3kg/m3.
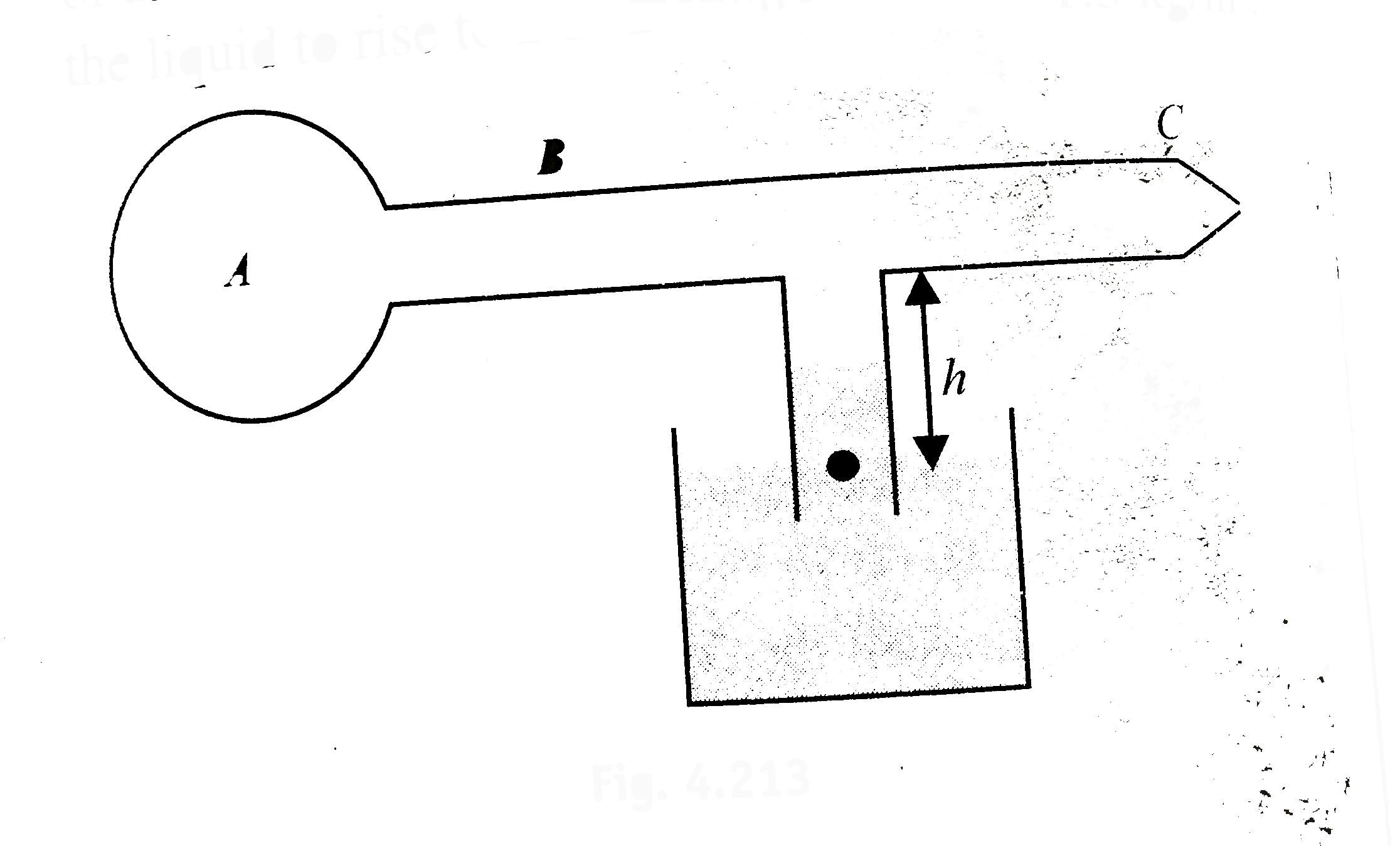View SolutionA liquid flows through two capillary tube under the same pressure head. The lengths of the tube are in the ratio 2:1 and the ratio of their diameters is 2:3. Compare the rates of flow of liquid through the tubes ?
View SolutionThe velocity of liquid flowing through a tube at certain distance from the axis of tube
View Solution_S01_083_Q01.png)
Water (density ρ) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)View SolutionAlcohol flows through two capillary tubes under a pressure lead. The diameter of the two tubes are in the ratio of 4:1 and the length are in the ratio of 1:4. Compare the rate of flow of alcohol through the two tubes.
View SolutionThe rate of flow of a liquid through a capillary tube of radius r is under a pressure difference of P. Calculate the rate of flow when the diameter is reduced to half and the pressure difference is made 4 P?
View SolutionA 60 watt bulb operates on 220 V supply. The current flowing through the bulb is
View Solution