A liquid of density ρ has to spray with help of aspirator pump at height H from liquid level as shown in figure. If gauge pressure inside bulb is P and density of air is σ then velocity of air in tube AB is

{P+ρgHσ2}12
{P−ρgHσ2}12
{P+αgHσ2}12
{P+αgHσ}12
The correct Answer is:A
PB+12σV2=PA+P

PB=PA+P−12σV2
=PA−ρgH
V=√2P+ρgHσ
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
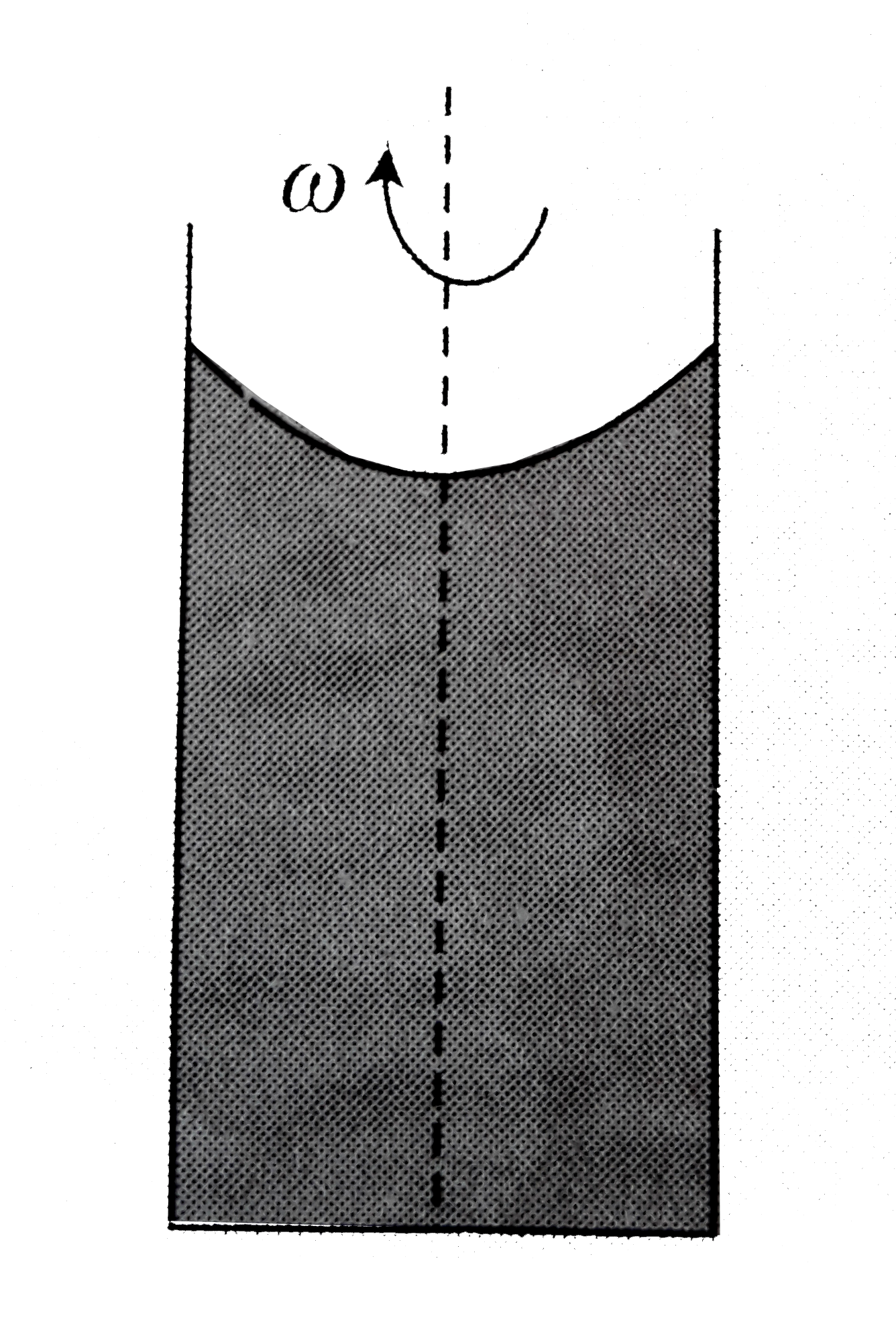 .
.
View SolutionA liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
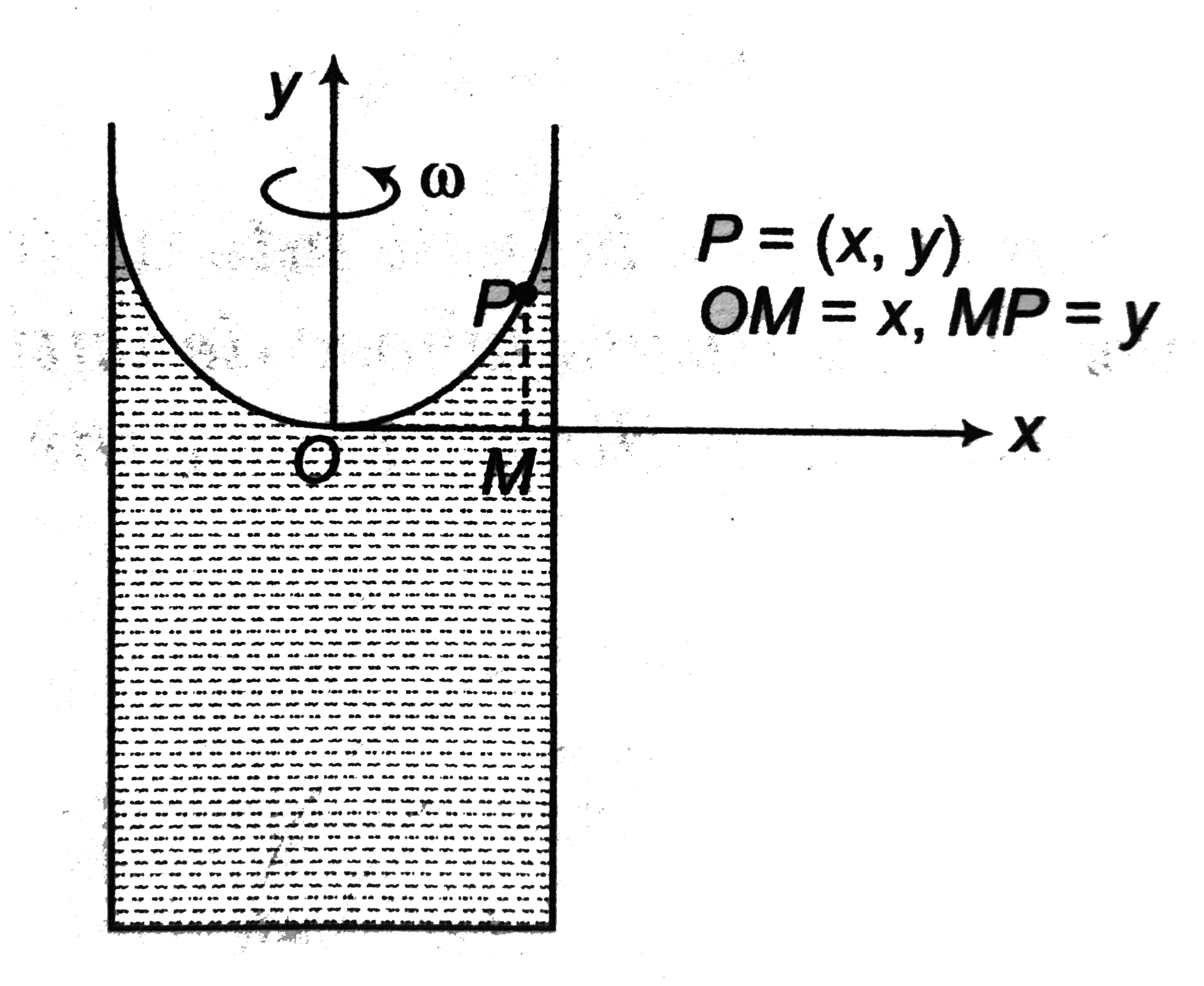 .
.
View Solution
Knowledge Check
Liquid of density ρ in a container exerts pressure P given by (height of liquid h and area A)
AP=AhρgBp=hρgCP=hρgADP=ρgAhA U-tube of cross section A and 2A contains liquid of density ρ. Initially, the liquid in the two arms are held with a level difference h as shown in figure. After being released the levels equalize after some time. The work done by gravity forces on the liquid in the process is :
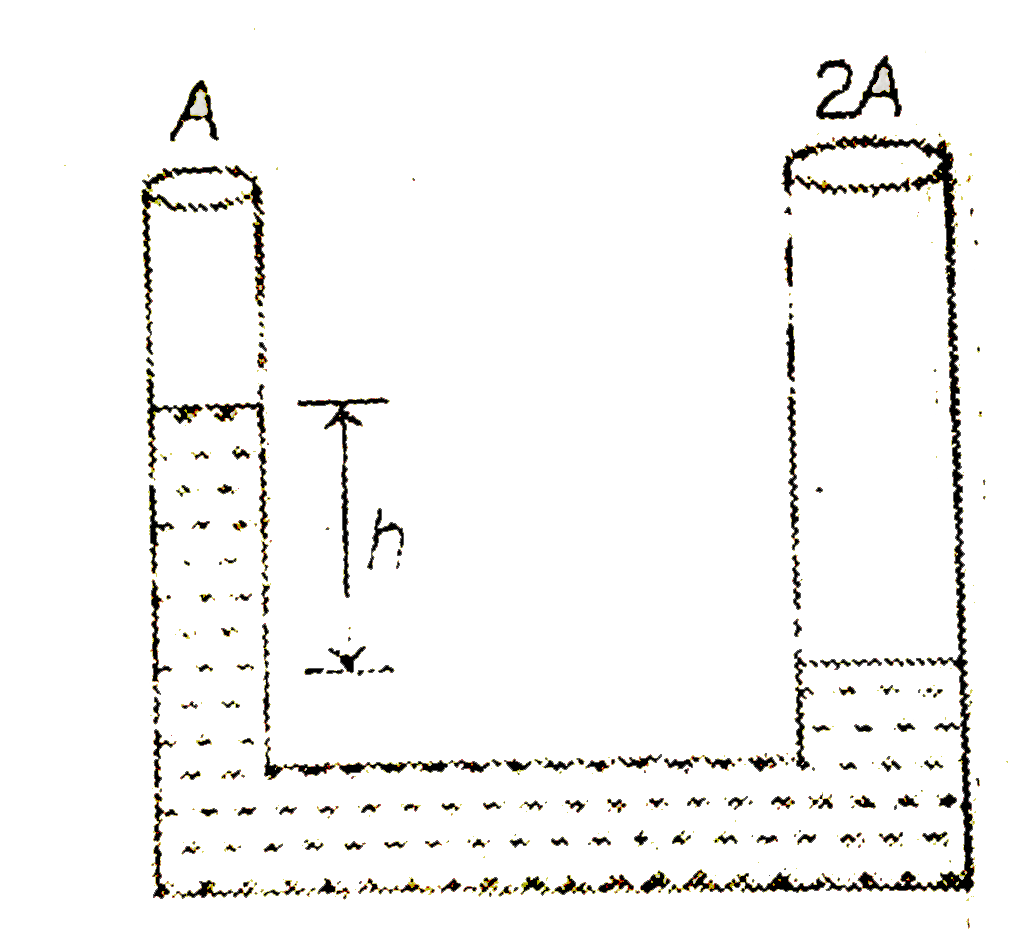 A23ρAgh2BρAgh2/3CρAgh2/6D34ρAgh2
A23ρAgh2BρAgh2/3CρAgh2/6D34ρAgh2A liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
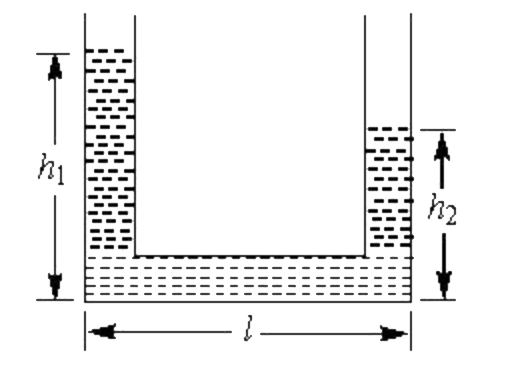 Ag(h1−h2)2l towards rightBg(h1−h2)2l towards leftCg(h1−h2)l towards rightDg(h1−h2)l towards left
Ag(h1−h2)2l towards rightBg(h1−h2)2l towards leftCg(h1−h2)l towards rightDg(h1−h2)l towards left
A liquid of density ρ is in a bucket that spins with angular velocity 'ω' as shown in figure. Prove that the free surface of the liquid has a parabolic shape. Find equation of this.
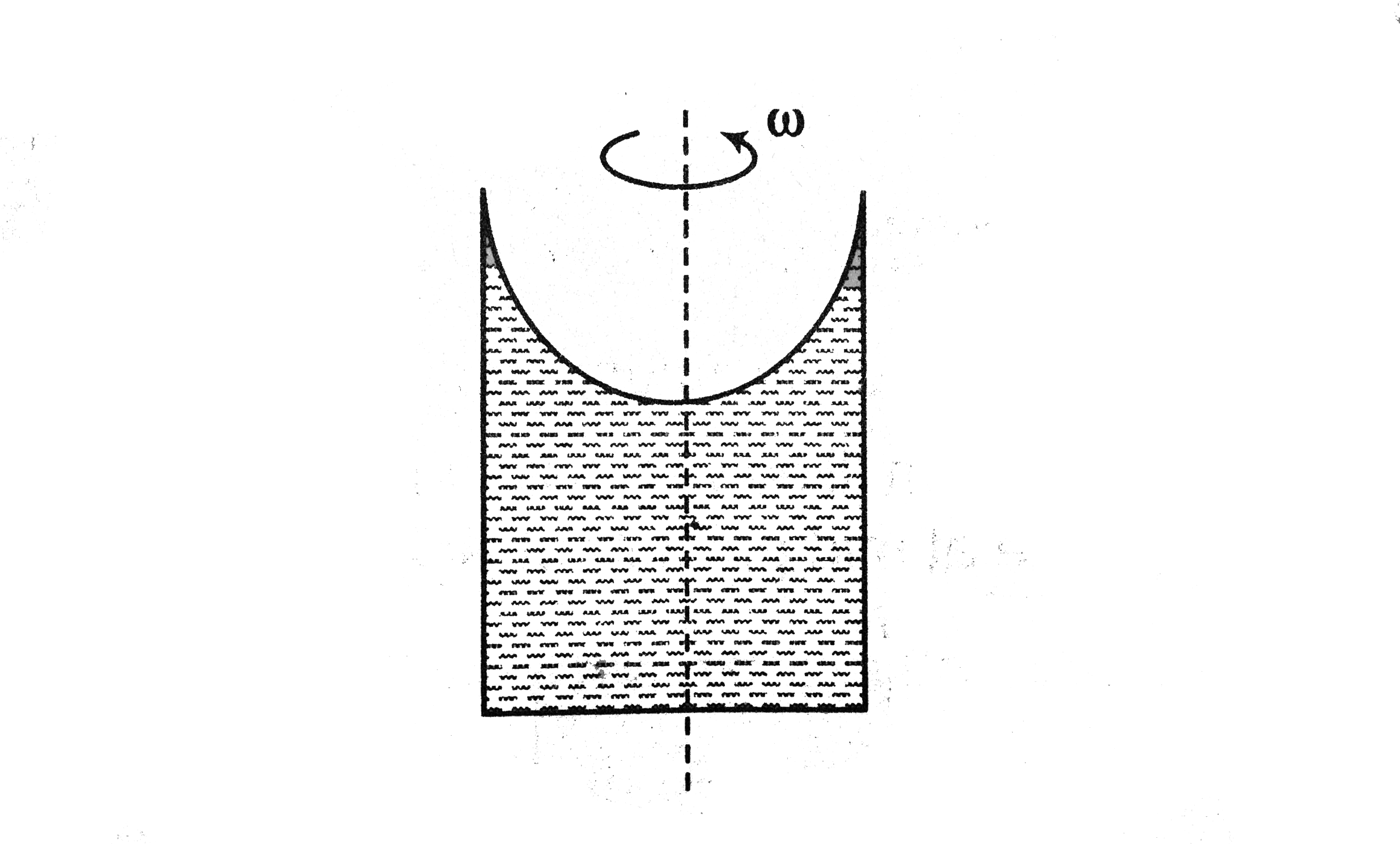 .
.
View SolutionA cylinder vessel containing a liquid of density ρ is closed by a smooth piston of mass m as shown. If atmospheric pressure is P0, radius of cylinder is r and height of liquid is h. Find
(a) Pressure of liquid just below the piston
(b) force at bottom of cylinder.
 .
.
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionA container shown in figure contains a liquid to depth H, and of density ρ The gauge pressure at point P is :
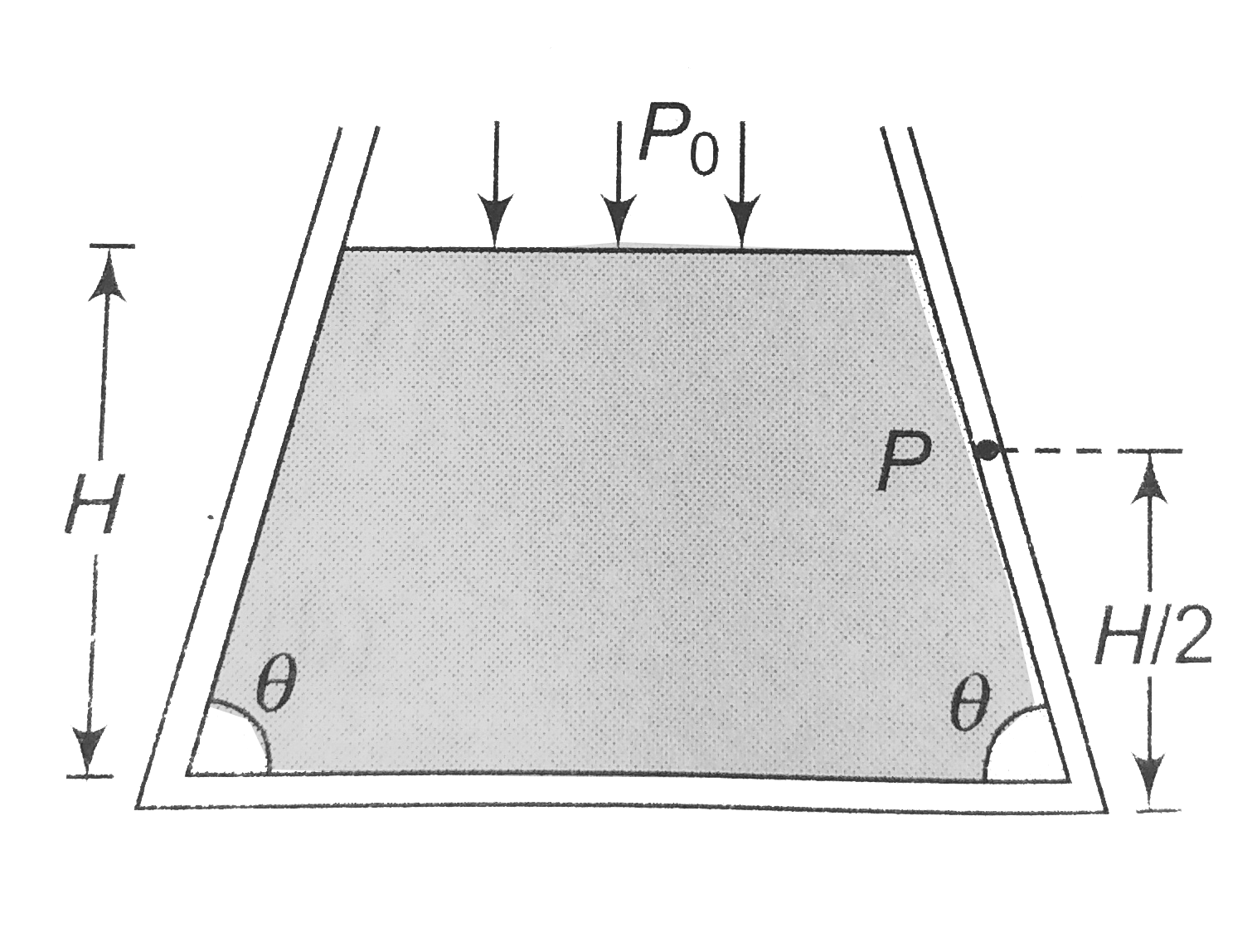
View Solution