Question

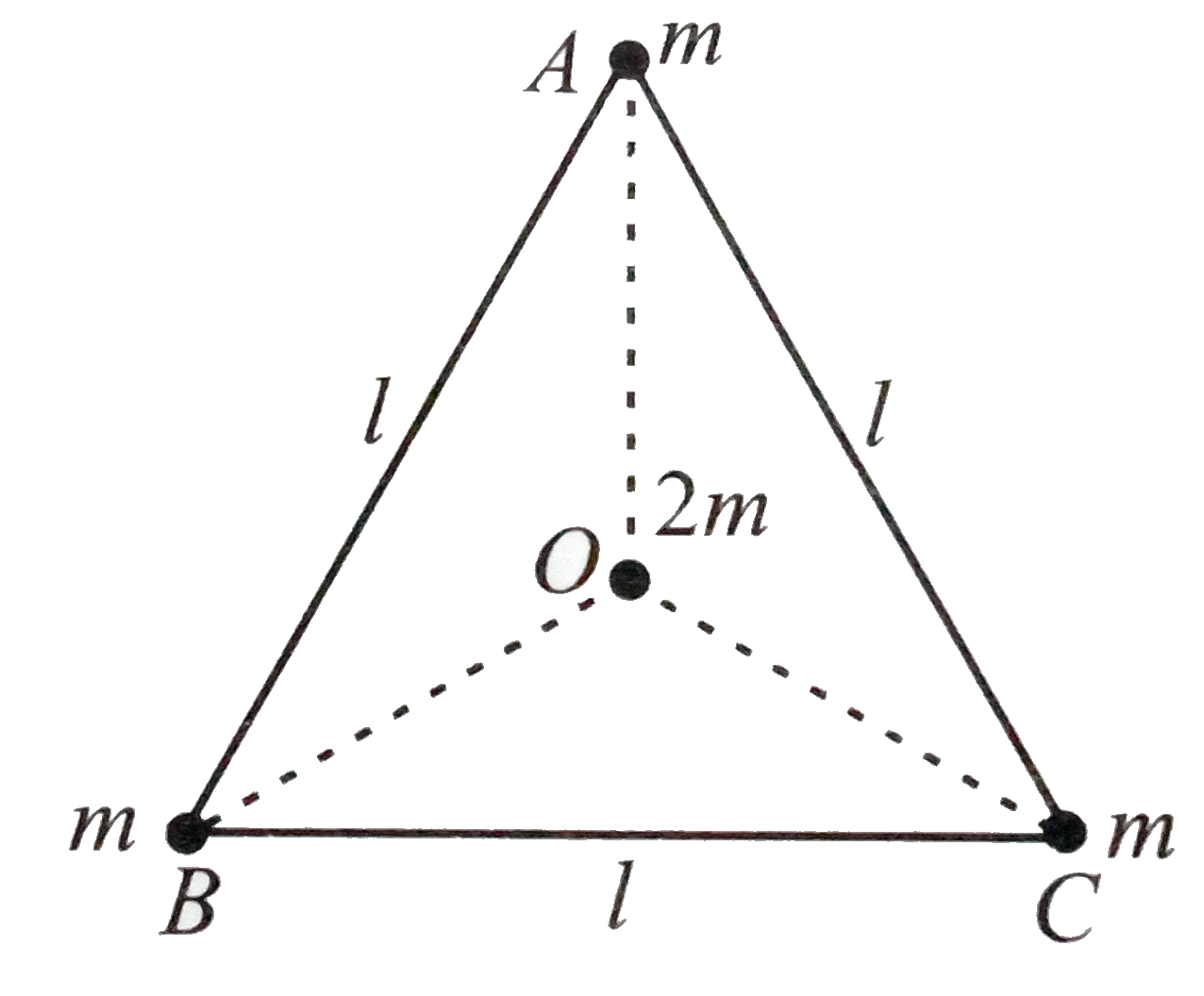
Three uniform rods, each of mass $M$ and length $l$, are connected to form an equilateral triangle in a gravity free space. Another small body of mass $m$ is kept at the centroid. Find the minimum velocity $v$ to be given to mass $m$ so that it escapes the gravitational pull of the triangle.

Explanation

To solve the problem of finding the minimum velocity $$v$$ required for the mass $$m$$ at the centroid of the equilateral triangle formed by three uniform rods to escape their gravitational pull, we will follow these steps:

Step 1: Understand the System
We have three uniform rods, each of mass \( M \) and length \( l \), arranged in the form of an equilateral triangle. A small mass \( m \) is placed at the centroid of this triangle. The goal is to determine the minimum velocity \( v \) that needs to be imparted to mass \( m \) so that it can escape the gravitational influence of the rods.

Step 2: Calculate the Gravitational Potential Energy
The gravitational potential energy \( U \) of the mass \( m \) due to the rods needs to be calculated. The potential energy due to a small element of mass \( dm \) from one of the rods at a distance \( r \) from mass \( m \) is given by:

\( dU = -k \frac{m \, dm}{r} \)

where \( k \) is the gravitational constant.

Step 3: Determine the Mass Element \( dm \)
Let \( \lambda \) be the mass per unit length of the rod. Thus, we have:

\( \lambda = \frac{M}{l} \)

For a small segment of the rod of length \( dx \), the mass is:

\( dm = \lambda \, dx = \frac{M}{l} \, dx \)

Step 4: Calculate the Distance \( r \)
The distance \( r \) from the mass \( m \) at the centroid to the element \( dx \) on the rod can be calculated using the Pythagorean theorem. If \( a \) is the perpendicular distance from the centroid to the side of the triangle, then:

\( r = \sqrt{a^2 + x^2} \)

Step 5: Integrate to Find Total Potential Energy
The total potential energy \( U \) from one rod can be found by integrating \( dU \) over the length of the rod. Since the triangle is symmetric, the total potential energy from all three rods is three times the potential energy from one rod.

\( U = 3 \int_0^{l/2} -k \frac{m \, \frac{M}{l} \, dx}{\sqrt{a^2 + x^2}} \)

Step 6: Solve the Integral
The integral can be solved, and we find:

\( U = -\frac{6k m M}{l} \ln\left(l + \sqrt{l^2 + 4a^2}\right) \)

Step 7: Apply Energy Conservation
For the mass \( m \) to escape the gravitational pull, the kinetic energy \( K \) must be equal to or greater than the potential energy \( U \):

\( \frac{1}{2} m v^2 \geq |U| \)

Substituting the expression for \( U \):

\( \frac{1}{2} m v^2 \geq \frac{6k m M}{l} \ln\left(l + \sqrt{l^2 + 4a^2}\right) \)

Step 8: Solve for Minimum Velocity \( v \)
Cancel \( m \) from both sides and solve for \( v \):

\( v^2 \geq \frac{12k M}{l} \ln\left(l + \sqrt{l^2 + 4a^2}\right) \)

Thus, the minimum velocity \( v \) is given by:

\( v = \sqrt{\frac{12k M}{l} \ln\left(l + \sqrt{l^2 + 4a^2}\right)} \)

Final Answer
The minimum velocity \( v \) required for mass \( m \) to escape the gravitational pull of the triangle is:

\( v = \sqrt{\frac{12k M}{l} \ln\left(l + \sqrt{l^2 + 4a^2}\right)} \)