Find the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
To find the gravitational potential due to a spherical shell of mass M and radius R at distances r<R and r>R, we can follow these steps:
Step 1: Gravitational Potential Inside the Shell (r<R)
1. Understanding the Shell Theorem: According to the shell theorem, the gravitational field inside a uniform spherical shell is zero. This means that if you are located anywhere inside the shell (at a distance r from the center, where r<R), the net gravitational force acting on you due to the shell is zero.
2. Gravitational Potential is Constant: Since the gravitational field E is zero inside the shell, the gravitational potential V must be constant throughout the interior of the shell.
3. Potential at the Surface: The gravitational potential at the surface of the shell (at distance R) can be calculated using the formula for the potential due to a point mass:
V(R)=−GMR
where G is the gravitational constant and M is the mass of the shell.
4. Conclusion for r<R: Therefore, the gravitational potential at any point inside the shell (for r<R) is equal to the potential at the surface:
V(r)=−GMRfor r<R
Step 2: Gravitational Potential Outside the Shell (r>R)
1. Using the Shell Theorem Again: For points outside the shell (where r>R), we can treat the entire mass M of the shell as if it were concentrated at a point at the center of the shell.
2. Potential Calculation: The gravitational potential at a distance r from the center of the shell is given by:
V(r)=−GMr
This formula is derived from the definition of gravitational potential due to a point mass.
3. Conclusion for r>R: Thus, the gravitational potential at any point outside the shell (for r>R) is:
V(r)=−GMrfor r>R
Summary of Results
- For r<R:
V(r)=−GMR
- For r>R:
V(r)=−GMr
V(R)=−GMR
where G is the gravitational constant and M is the mass of the shell.
V(r)=−GMRfor r<R
V(r)=−GMr
This formula is derived from the definition of gravitational potential due to a point mass.
V(r)=−GMrfor r>R
- For r<R:
V(r)=−GMR
- For r>R:
V(r)=−GMr
Similar Questions
A point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View Solution
Knowledge Check
- Question 1 - Select One
Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
A B
B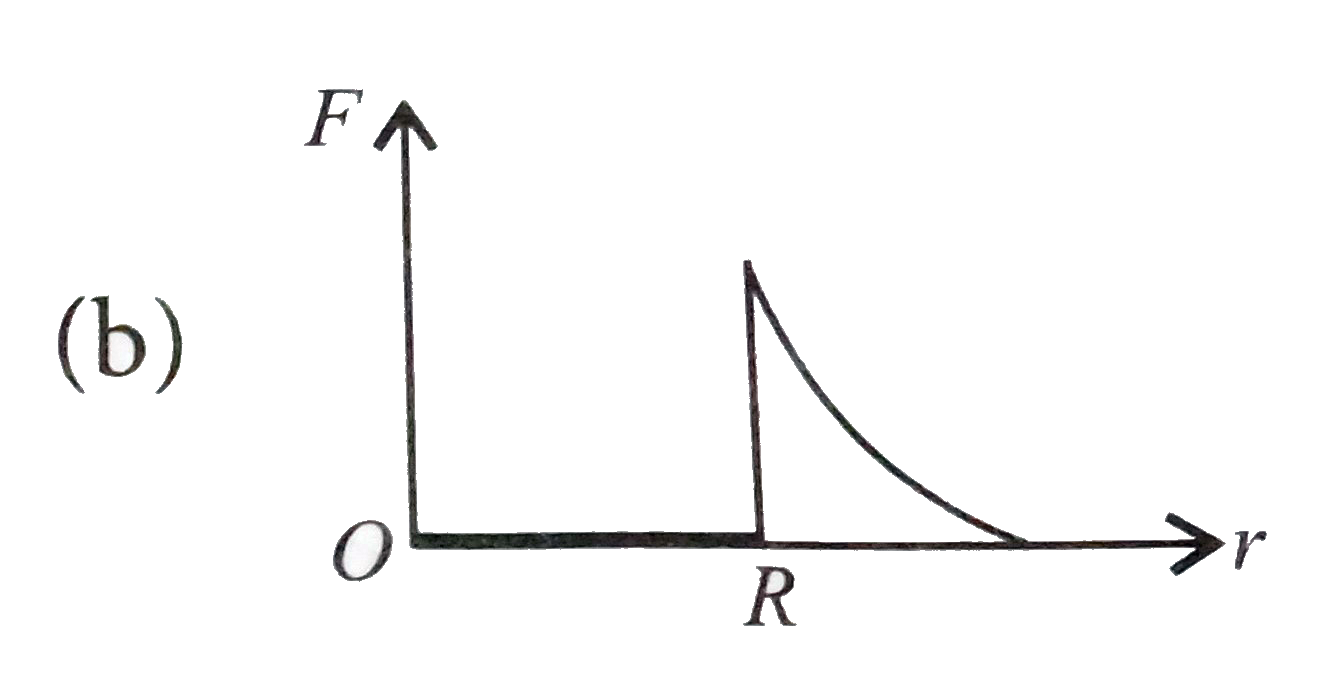 C
C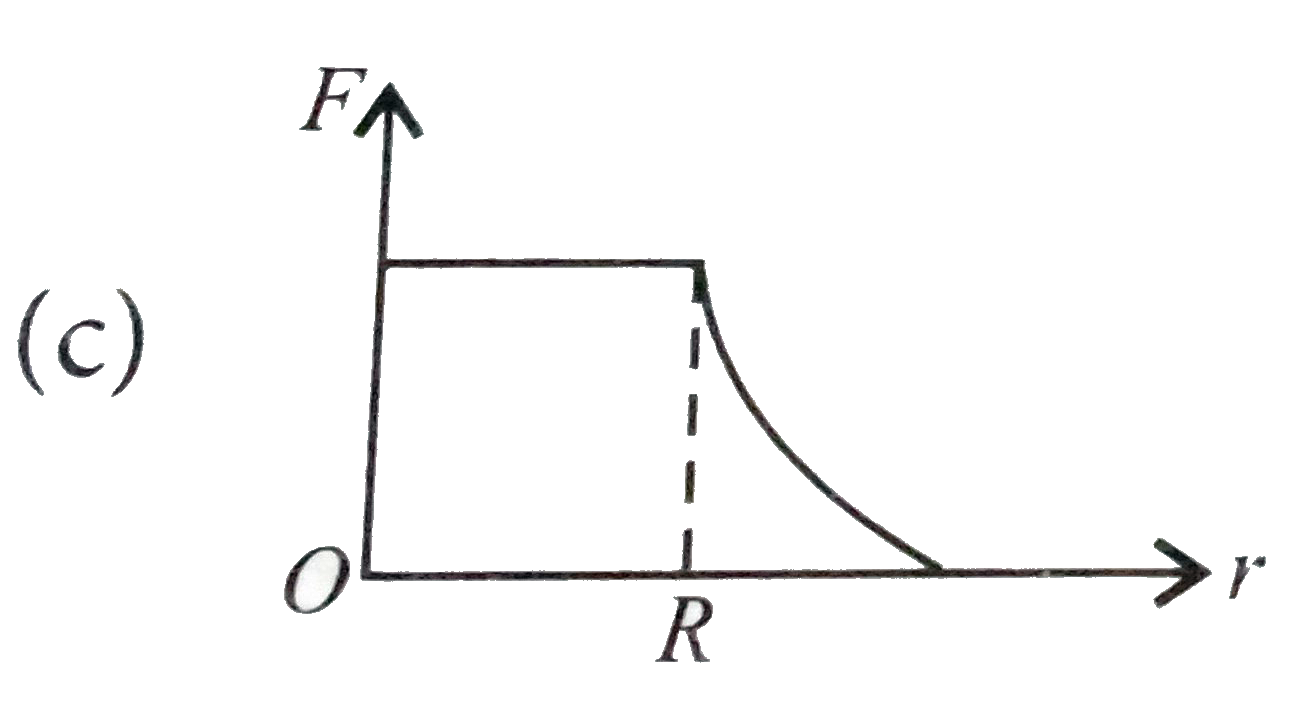 D
D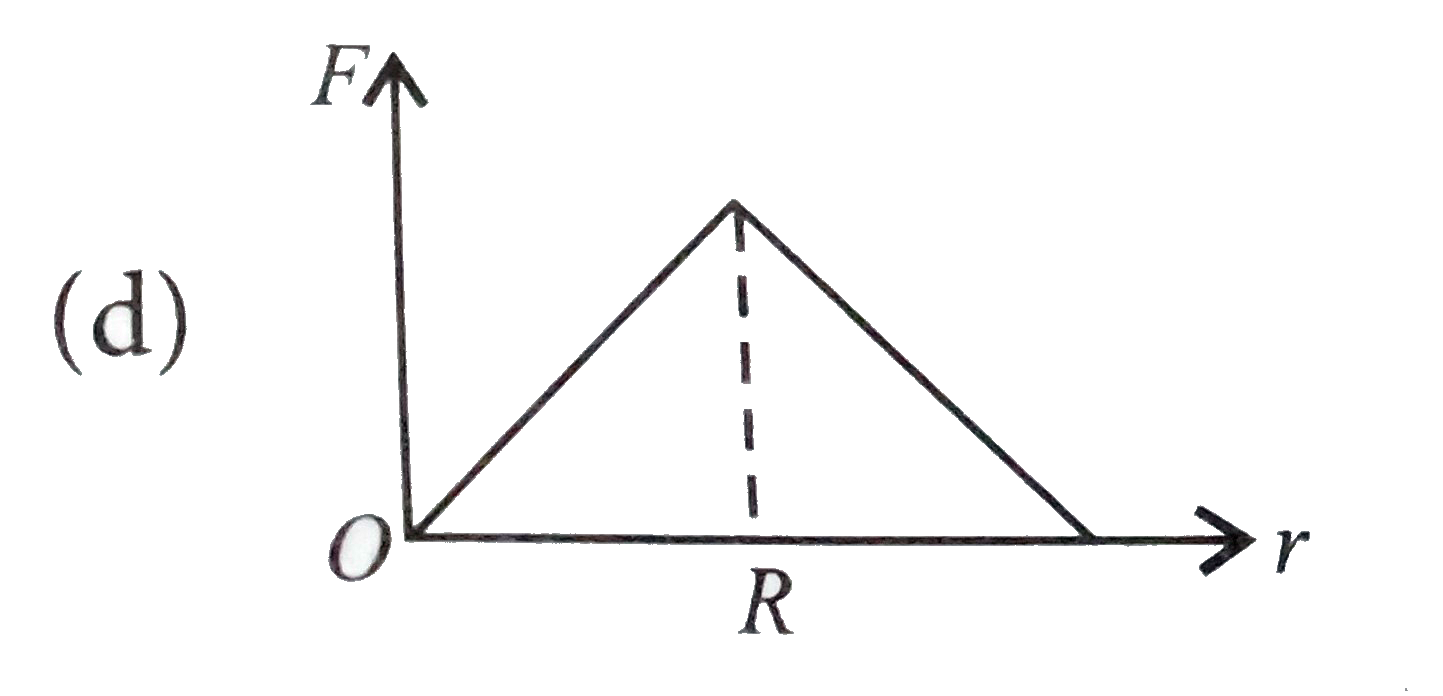
Using Gauss' law deduce the expression for the electric field due to a uniformly charged sperical conducting shell of radius R at a point (i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r>Randr<R. (r being the distance from the centre of the shell)View SolutionFigure shows a hemispherical shell of mass M and radius R and a concentric shell of mass m and radius 3R/4.
 View Solution
View SolutionA thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R.The distance r<R.The electric potential at the centre of the shell will be
 View Solution
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R fro the centre of the shell. The electric potential at the centre of shell will (potential at infinity is zero).
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View Solution

