In some region, the gravitational field is zero. The gravitational potential in this region
must be variable
must be constant
can not be zero
must be zero
The correct Answer is:B
To solve the question, we need to analyze the relationship between gravitational field and gravitational potential.
1. Understanding Gravitational Field and Potential:
The gravitational field (E) is related to the gravitational potential (V) by the equation:
E=−dVdr
where dVdr is the gradient (or derivative) of the gravitational potential with respect to distance.
2. Given Condition:
The problem states that in a certain region, the gravitational field is zero:
E=0
3. Implication of Zero Gravitational Field:
If the gravitational field is zero, substituting into the equation gives:
0=−dVdr
This implies that:
dVdr=0
4. Conclusion about Gravitational Potential:
The condition dVdr=0 means that the gravitational potential V does not change with respect to distance r. Therefore, the gravitational potential must be constant in that region.
5. Constant Value of Gravitational Potential:
The constant value of gravitational potential can either be zero or some non-zero value. However, the key point is that it does not vary; it remains constant.
6. Final Answer:
Thus, we conclude that the gravitational potential in the region where the gravitational field is zero must be constant.
Answer:
The gravitational potential in this region must be constant.
The gravitational field (E) is related to the gravitational potential (V) by the equation:
E=−dVdr
where dVdr is the gradient (or derivative) of the gravitational potential with respect to distance.
The problem states that in a certain region, the gravitational field is zero:
E=0
If the gravitational field is zero, substituting into the equation gives:
0=−dVdr
This implies that:
dVdr=0
The condition dVdr=0 means that the gravitational potential V does not change with respect to distance r. Therefore, the gravitational potential must be constant in that region.
The constant value of gravitational potential can either be zero or some non-zero value. However, the key point is that it does not vary; it remains constant.
Thus, we conclude that the gravitational potential in the region where the gravitational field is zero must be constant.
The gravitational potential in this region must be constant.
Similar Questions
Knowledge Check
Gravitational potential energy = ....
AmghB12mv2C2mghDnone of these
Two bodies of masses M1 and M2 are kept separeated by a distance d. The potential at the point where the gravitational field produced by them is zero,the gravitational potential will be :-
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
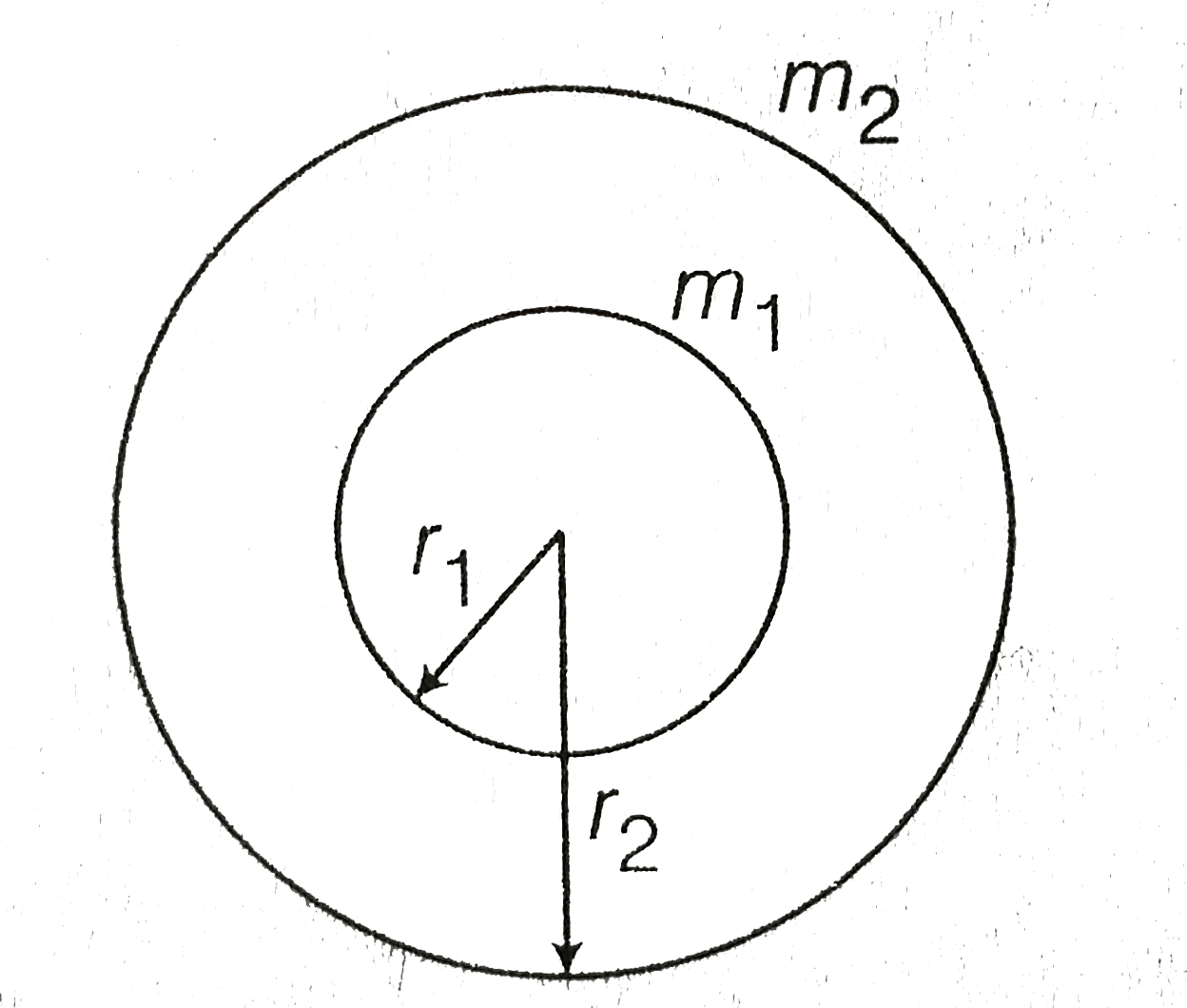
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionDefine gravitational potential and gravitational potential energy.
View SolutionObtain an expression for the gravitational potential.
View SolutionThe gravitational potential energy is maximum at :
View SolutionTwo point masses m and 2m are kept at points A and B as shown. E represents magnitude of gravitational field strength and V the gravitational potential. As we move from A to B

View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
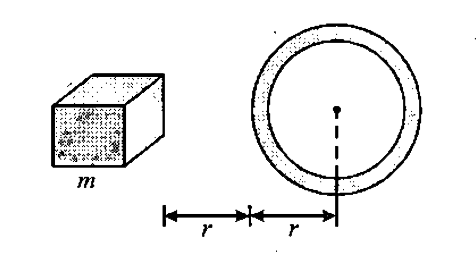
A. only gravitational field inside the shell is zero
B. gravitational field and gravitational potential both are zero inside the shell
C. gravitational potential as well as gravitational field inside the shell are not zero .
D. can't be ascertained
View Solution
