Two point masses m and 2m are kept at points A and B as shown. E represents magnitude of gravitational field strength and V the gravitational potential. As we move from A to B

E will first decreases then increases
E will first increases then decreases
V will first decreases then increases
V will first increases then decrease
The correct Answer is:A, D
E due to point mass is E=Gmr2
As r→0,E→∝
So, just over the point masses, E=∞. Hence, in moving from one point mass to other point mass, E first decreases and then increases.
V due to a point mass is
V=−Gmr
As r→0,V→−∞
So, just over the point mass, V is −∞. Hence, in moving from one point mass to other point mass, V first increase and then decrease .
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective14videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.120videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct22videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
Three point masses 'm' each are kept at three verties of a square pf side 'a' as shown in figure. Find gravitation potential and field strength at point O.
 .View Solution
.View SolutionTwo bodies of masses M1 and M2 are kept separeated by a distance d. The potential at the point where the gravitational field produced by them is zero,the gravitational potential will be :-
View SolutionTwo particles of masses 'm' and '9m' are separated by a distance 'r'. At a point on the line joining them the gravitational field is zero. The gravitational potential at that point is (G = Universal constant of gravitation)
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
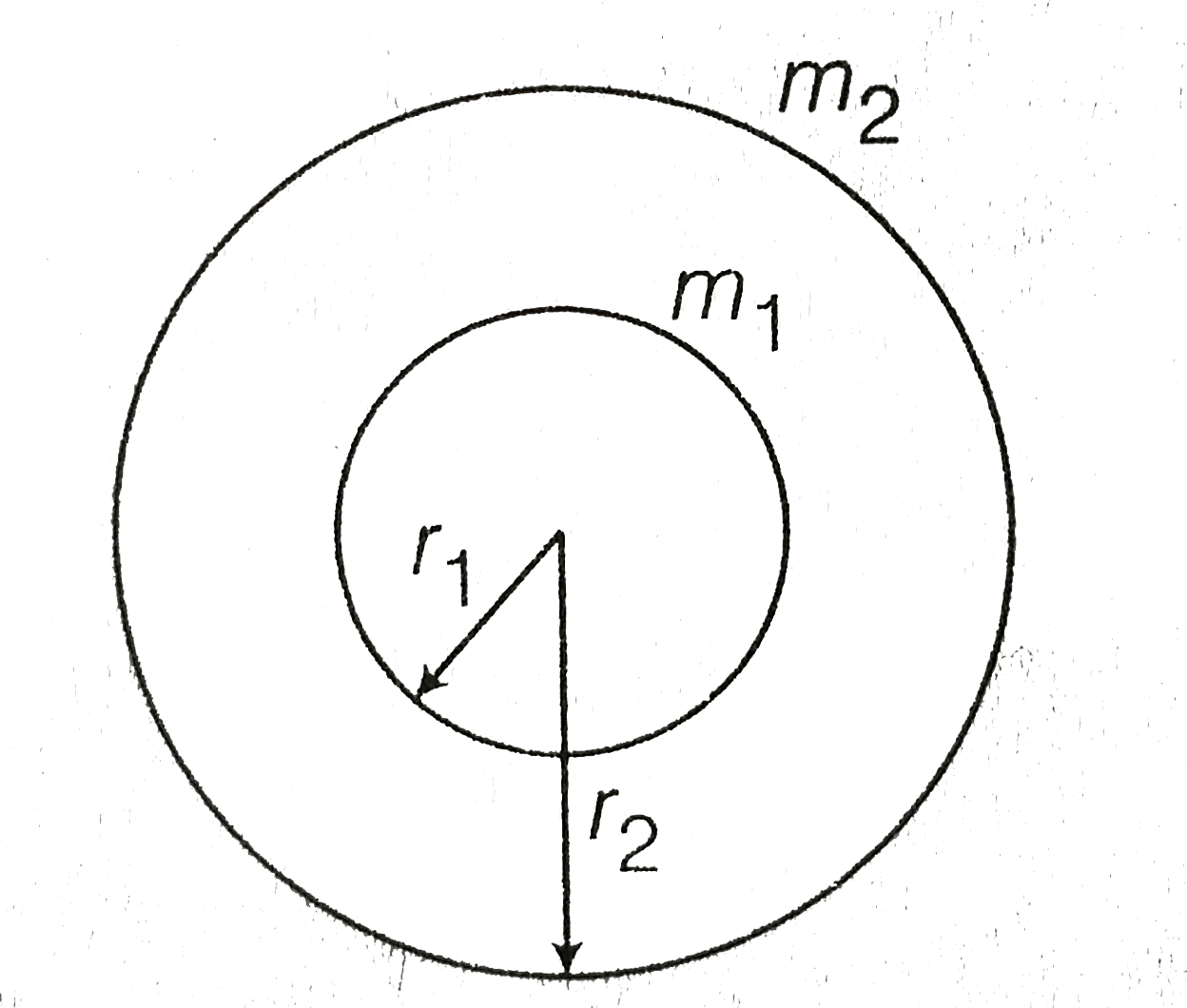
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).View SolutionLet V and E denote the gravitational potential and gravitational field at a point. It is possile to have
View SolutionIf gravitational potential is V=xy2, find the gravitational field at (2,1)
View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionTwo points masses m each are kept at the two verticle of an equilateral triangle of side 'a' as shows in figure.

Find gravitational potential and magnitude of field strength at O.View SolutionTwo concentric speherical shells are as shown in figure. The magnitude of gravitational potential (V) and field strength (E ) vary with distance ( r) from centre as
 View Solution
View SolutionTwo point masses having mass m and 2m are placed at distance d . The point on the line joining point masses , where gravitational field intensity is zero will be at distance
View Solution

