Relationship between angular momentum L and kinetic energy E of a rigid body in pure rotation is
E=L2/2I
E2=2I/L
L=E2/2I
E = 2IL
The correct Answer is:A
E=12Iω2 [∵L=Iω]
∴ E=L22I
Similar Questions
Knowledge Check
- Question 1 - Select One
Angular momentum L and rotational kinetic energy KR of a body are related to each other by the relation. (I = moment of inertia)
A1. KR = 2ILB2. KR=L22IC3. KR=2ILD4. KR=L2I
If the angular momentum of a body increases by 50%, its kinetic energy of rotation increases by
View SolutionIf J is the angular momentum and E is the kinetic energy, then J2E has the dimensions of
View SolutionA body is rotating with angular momentum L. If I is its moment of inertia about the axis of rotation is I, its kinetic energy of rotation is
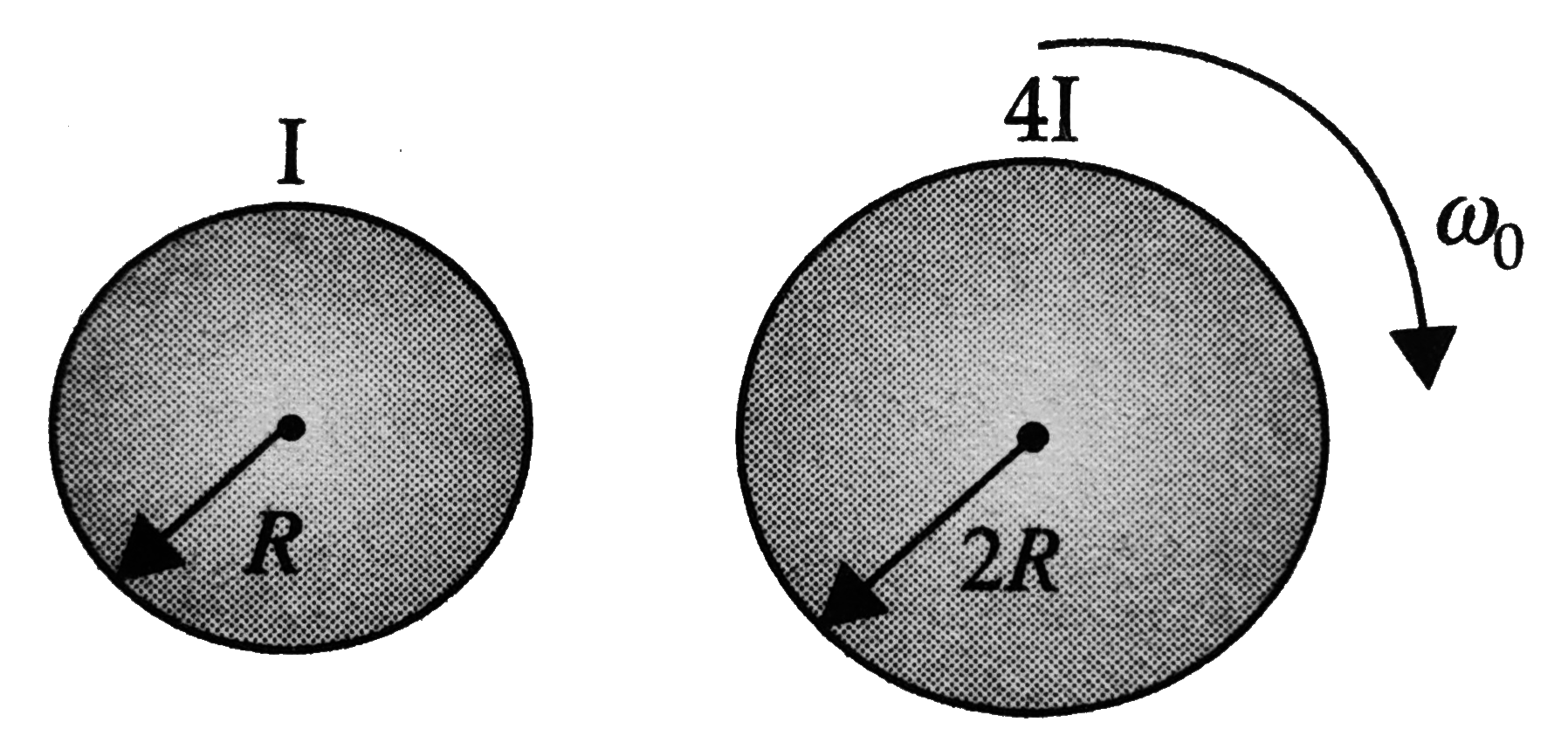
View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
(A) angular momentum of system is conserved
(B) kinetic energy is conserved
(C neither the angular momentum nor the kinetic energy is conserved
(D) both the angular momentum and kinetic energy are conserved
 View Solution
View SolutionA planet is revolving around the sun in an elliptical orbit. Which out of the following remains constant.
(a) Linear speed (b) angular momentum
( c) kinetic energy (d) potential energy (e) total energy throughout its orbit.View SolutionOn what factors does the kinetic energy of a purely rotating body depend?
View SolutionA rigid body rotates with an angular momentum L. If its rotational kinetic energy is made 4 times, its angular momentum will become
View Solution

