The parallel axis theorem can be applied to
any two parallel axes
any two parallel-axes of which one must lie within the body
any two parallel-axes of which one must pass through the centre of mass of the body.
any two parallel axes lying in the plane of the body
The correct Answer is:C
Step-by-Step Solution:
1. Understanding the Parallel Axis Theorem: The parallel axis theorem is a principle in rotational mechanics that allows us to calculate the moment of inertia of a body about any axis parallel to an axis through its center of mass.
2. Identifying the Axes: Let's denote two axes:
- Axis 1 (ICM): This axis passes through the center of mass (CM) of the body.
- Axis 2 (Ip): This axis is parallel to Axis 1 and is located at a distance 'd' from it.
3. Moment of Inertia Calculation: According to the parallel axis theorem, the moment of inertia (Ip) about Axis 2 can be expressed as:
Ip=Icm+m⋅d2
where:
- Icm is the moment of inertia about the center of mass axis (Axis 1).
- m is the mass of the body.
- d is the distance between the two parallel axes.
4. Application Conditions: The theorem can be applied to any rigid body, whether it is two-dimensional or three-dimensional, as long as:
- One of the axes must pass through the center of mass.
- The two axes must be parallel.
5. Conclusion: Therefore, the parallel axis theorem can be applied to any two parallel axes where one axis is through the center of mass of the body.
Final Answer:
The parallel axis theorem can be applied to any two parallel axes, provided that one of them passes through the center of mass of the body.
---
- Axis 1 (ICM): This axis passes through the center of mass (CM) of the body.
- Axis 2 (Ip): This axis is parallel to Axis 1 and is located at a distance 'd' from it.
Ip=Icm+m⋅d2
where:
- Icm is the moment of inertia about the center of mass axis (Axis 1).
- m is the mass of the body.
- d is the distance between the two parallel axes.
- One of the axes must pass through the center of mass.
- The two axes must be parallel.
The parallel axis theorem can be applied to any two parallel axes, provided that one of them passes through the center of mass of the body.
Similar Questions
Assertion : Moment of inertia about an axis passing throught centre of mass is always minimum
Reason : Theorem of parallel axis can be applied for 2-D as well as 3-D bodies.
View SolutionAssertion : Moment of inertia about an axis passing throught centre of mass is always minimum
Reason : Theorem of parallel axis can be applied for 2-D as well as 3-D bodies.
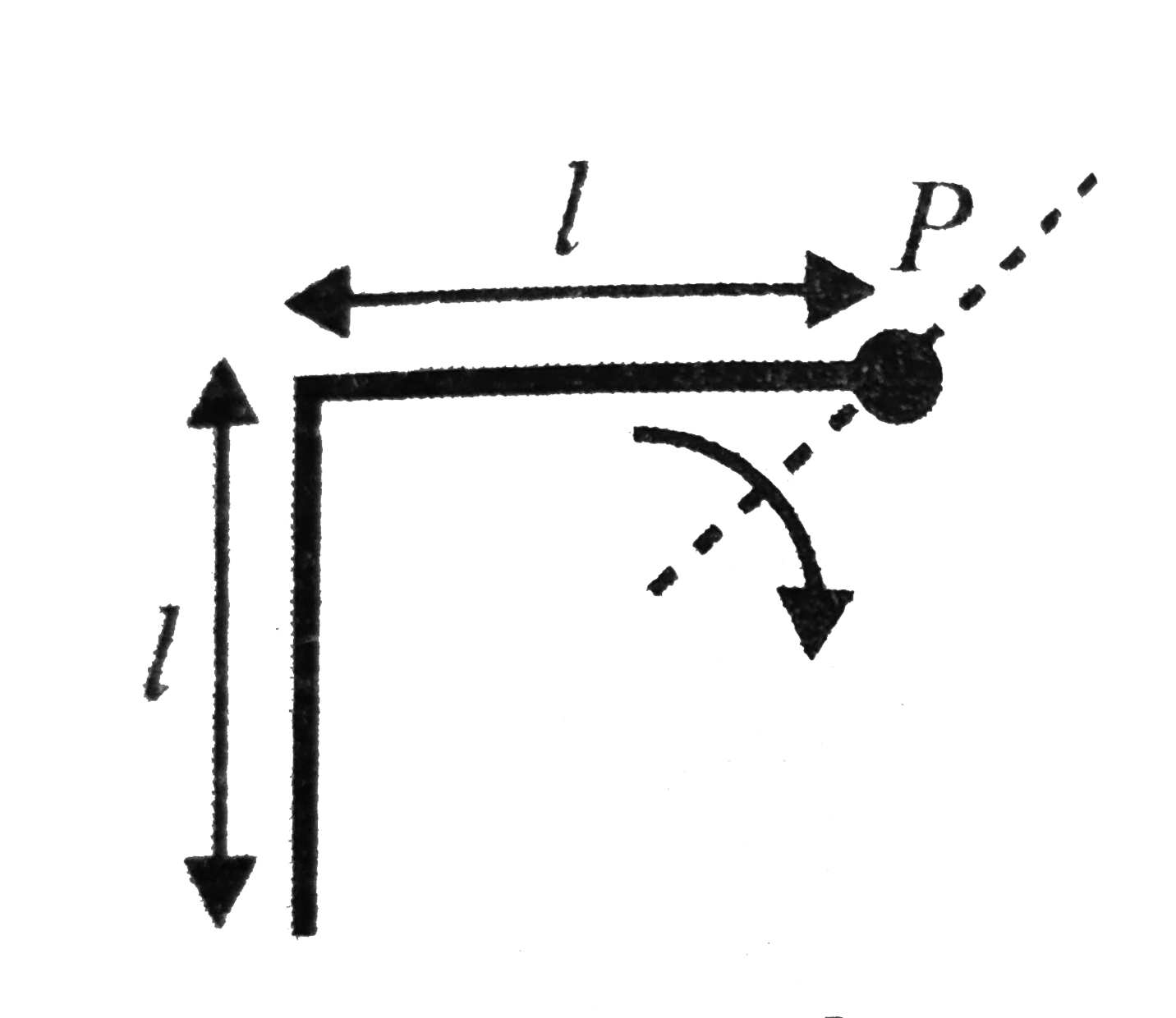
View SolutionFind the moment of inertia of the two uniform joint rods about point P as shown in Fig. Use parallel axis theorem. Mass of each rod is M.
View SolutionUse the parallel axis theorem to find the moment of inertia ofa uniform rod of mass M = 3kg and length 2a (a = 1m), about a perpendicular axis through one end?
View SolutionUsing the parallel axes theorem, find the M.I. of a sphere of mass m about an axis that touches it tangentially. Given that Icm=25mr2
View SolutionIf f(x)=xαlogx and f(0)=0, then the value of ′α′ for which Rolle's theorem can be applied in [0,1] is (A) -2 (B) -1 (C) 0 (D) 12
View SolutionRolle’s theorem can not applicable for :
View SolutionState (i) parallel axes theorem and (ii) perpendicular axes theorem.
View SolutionAssertion : With the help of Gauss's theorm we can find electric field at any point.
Reason : Gauss's theorem can be applied for any type of charge distribution.
View SolutionLaw of mass action can not be applied to
View Solution
