Question

State and prove parallel axis theorem

Explanation

Parallel axis theorem: Parallel axis theorem states that the moment of inertia or a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of mass and the product of the mass of the body and the square of the perpendicular distance between the two axes.
If `I_C` is the moment of incrliu oflhe body of mass M about an axis passing through the center of mass then the moment of inertia I about a parallel axis at a distance d from it is given by the relation
` I = I_C = md^2`
`I=I_C + Md^2`
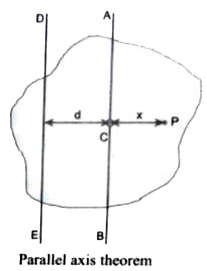
Let us consider a rigid body as shown in figure. Its moment of inertia about an axis AB passing through the center of mass is `I_C` . DE is another axis parallel to AB at a perpendicular distance d from AB. The moment of inertia of the body about DE is I . We attempt to get an expression for I in terms of `I_C` . For this, let us consider a point mass m on the body at position x from its center of mass
The moment of inertia of the point mass about the axis DE is `m(x +d)^2` The moment of inertia I of the whole body about DE is the summation of the above expression.
` I = sum m (x+d)^2`
This equation could further be written as,
` I sum m (x^2 + d^2 + 2xd)`
`I = sum (mx^2 +md^2 + 2dmx)`
`I = sum mx^2 + sum md^2 + 2d sum mx `
Here `sum mx^2` is the moment of inertia of the body about the center of mass. Hence . `I_C = sum mx^2`
The term `sum mx = 0` because, x can take positive and negative values with respect to the axis AB. The summation `(sum mx)` will be zero .
Thus `I=I_C + (sum mx)` will be zero .
Thus `I = I_C + sum md^2 = I_C + (sum m)d^2`
Here ` sum m ` is the entire mass M of the object `(sum m = m )`
`I = I_C + Md^2`