A sphere is moving at some instant with horizontal velocity v0 in right and angular velocity ω in anti clockwise sense. If |v0|=|ωR|, the instantaneous centre of rotation is
at the bottom of the sphere
at the top of the sphere
at the centre of the sphere
anywhere inside the sphere
The correct Answer is:B
To solve the problem, we need to find the instantaneous center of rotation of a sphere that is rolling with a horizontal velocity v0 to the right and an angular velocity ω in the anticlockwise direction. We are given that |v0|=|ωR|, where R is the radius of the sphere.
1. Understanding the Motion:
- The sphere is rolling on a smooth surface. The horizontal velocity v0 is directed to the right, and the angular velocity ω is directed in the anticlockwise direction.
2. Relating Linear and Angular Velocities:
- The linear velocity at the point of contact with the ground due to rotation is given by ωR. Since |v0|=|ωR|, the linear velocity of the center of mass v0 is equal to the linear velocity due to rotation at the bottom point of the sphere.
3. Finding the Instantaneous Center of Rotation:
- The instantaneous center of rotation is the point on the sphere where the velocity is zero at that instant. For rolling without slipping, this point is located at the bottom of the sphere when the sphere rolls to the right.
- However, since v0=ωR, the sphere is not just rolling; it is also translating. We need to find a point where the translational velocity v0 cancels out the rotational velocity ωR.
4. Analyzing the Velocity Components:
- The point at the bottom of the sphere (point of contact) has a velocity of ωR directed to the left (due to rotation).
- The center of mass of the sphere is moving to the right with velocity v0.
- To find the instantaneous center of rotation, we can consider a point above the center of the sphere where the leftward velocity component due to rotation cancels out the rightward velocity of the center of mass.
5. Determining the Position of the Instantaneous Center:
- Let’s denote the instantaneous center of rotation as point P. The velocity at point P can be expressed as:
vP=v0−ωR
- Setting vP=0 gives us:
v0−ωR=0⟹v0=ωR
- This means that point P is located directly above the center of the sphere, at a distance R from the center.
6. Conclusion:
- Therefore, the instantaneous center of rotation is at the top of the sphere.
Final Answer:
The instantaneous center of rotation is at the top of the sphere.
- The sphere is rolling on a smooth surface. The horizontal velocity v0 is directed to the right, and the angular velocity ω is directed in the anticlockwise direction.
- The linear velocity at the point of contact with the ground due to rotation is given by ωR. Since |v0|=|ωR|, the linear velocity of the center of mass v0 is equal to the linear velocity due to rotation at the bottom point of the sphere.
- The instantaneous center of rotation is the point on the sphere where the velocity is zero at that instant. For rolling without slipping, this point is located at the bottom of the sphere when the sphere rolls to the right.
- However, since v0=ωR, the sphere is not just rolling; it is also translating. We need to find a point where the translational velocity v0 cancels out the rotational velocity ωR.
- The point at the bottom of the sphere (point of contact) has a velocity of ωR directed to the left (due to rotation).
- The center of mass of the sphere is moving to the right with velocity v0.
- To find the instantaneous center of rotation, we can consider a point above the center of the sphere where the leftward velocity component due to rotation cancels out the rightward velocity of the center of mass.
- Let’s denote the instantaneous center of rotation as point P. The velocity at point P can be expressed as:
vP=v0−ωR
- Setting vP=0 gives us:
v0−ωR=0⟹v0=ωR
- This means that point P is located directly above the center of the sphere, at a distance R from the center.
- Therefore, the instantaneous center of rotation is at the top of the sphere.
The instantaneous center of rotation is at the top of the sphere.
Similar Questions
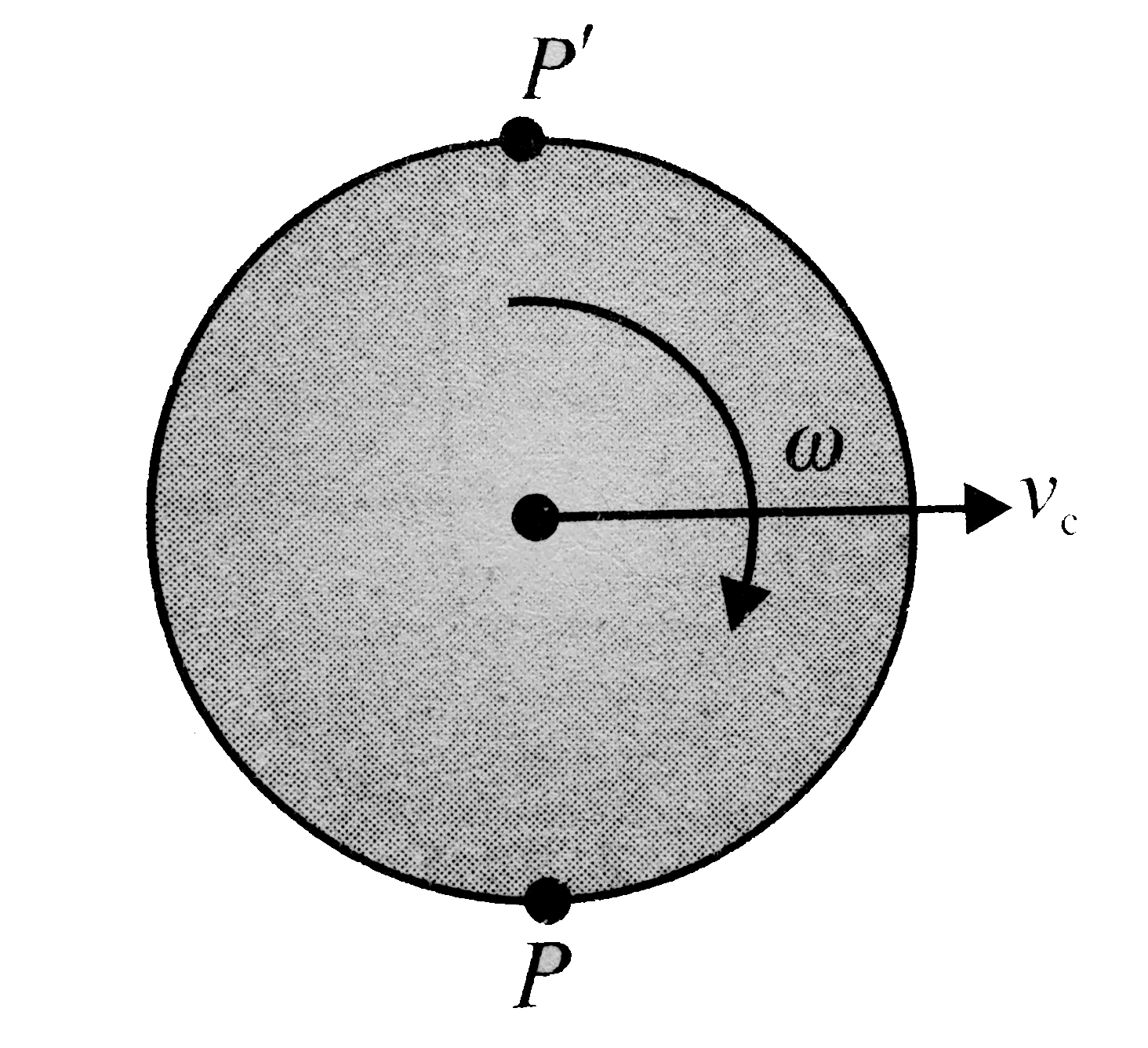
A sphere is moving towards the positive x-axis with a velocity vc and rotates clockwise with angular speed ω shown in Fig. such that vc>ωR. The instantaneous axis of rotation will be
View SolutionA sphere of mass M and radius r shown in the figure on a rough horizontal plane. At some instant it has translational velocity v0, and rotational velocity about centre v0/2r. The percentage change of translational velocity after the sphere start pure rolling:

View SolutionA uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position if
View SolutionA particle moves with initial velocity v0 and retardation αv, where v is velocity at any instant t. Then the particle
View SolutionIn the above question if the coil rotates with a constant angular velocity ω, the EMF induced in it
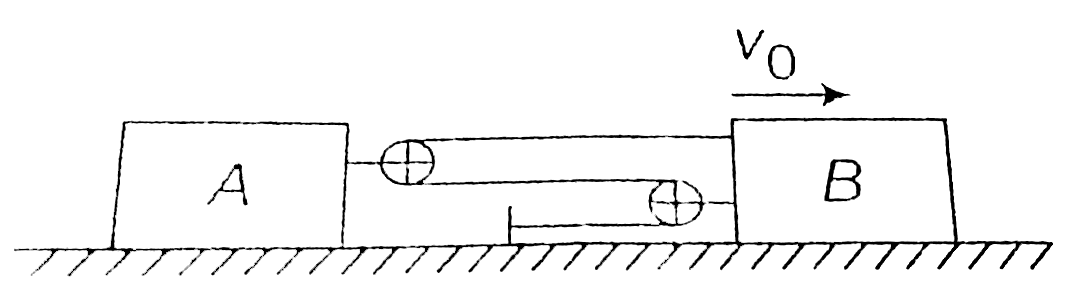
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is
View Solutiona uniform circular disc of radiu8s r placed on a roughn horizontal plane has initial velocity v0 and an angul,ar velocity ω0 has shown The disc comes to rest after moving some distance in the direction of motion. Then

View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
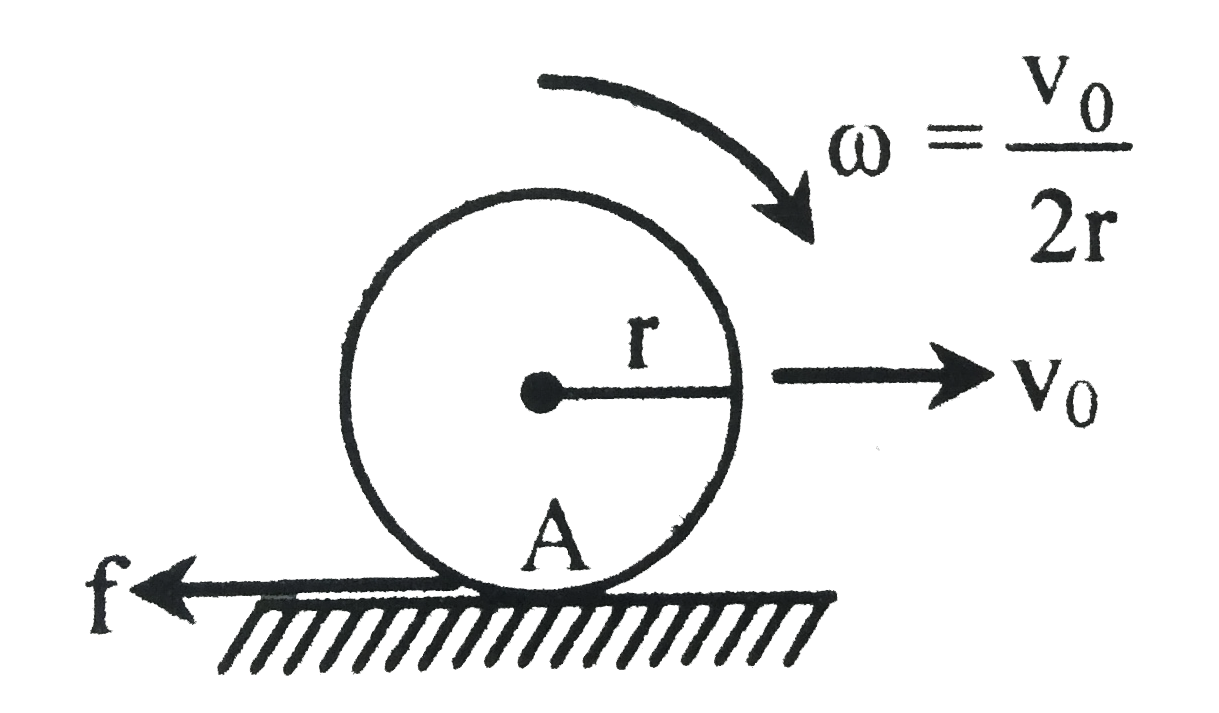
View SolutionA sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
 .
.
View Solution
