Which arises first , strain or stress ?
To determine which arises first, strain or stress, we can analyze the relationship between the two concepts in the context of elasticity. Here’s a step-by-step solution:
Step 1: Understanding Stress
Stress is defined as the force applied per unit area on an object. It is mathematically expressed as:
Stress=FA
where F is the force applied, and A is the cross-sectional area.
Step 2: Application of Force
When a force is applied to a material, it creates an internal resistance to deformation. This internal resistance is what we refer to as stress. Therefore, the application of force leads to the generation of stress within the material.
Step 3: Understanding Strain
Strain, on the other hand, is the measure of deformation representing the displacement between particles in a material body. It is defined as the change in length divided by the original length:
Strain=ΔLL0
where ΔL is the change in length and L0 is the original length.
Step 4: Relationship Between Stress and Strain
According to Hooke's Law, stress is directly proportional to strain within the elastic limit of a material:
Stress=E×Strain
where E is Young's modulus of the material. This relationship indicates that stress must occur before strain can be measured.
Step 5: Conclusion
From the analysis, we conclude that stress arises first when a force is applied to a material, which then leads to the generation of strain as a result of that stress. Therefore, stress precedes strain in the process of deformation.
Final Answer
Stress arises first, followed by strain.
---
Stress is defined as the force applied per unit area on an object. It is mathematically expressed as:
Stress=FA
where F is the force applied, and A is the cross-sectional area.
When a force is applied to a material, it creates an internal resistance to deformation. This internal resistance is what we refer to as stress. Therefore, the application of force leads to the generation of stress within the material.
Strain, on the other hand, is the measure of deformation representing the displacement between particles in a material body. It is defined as the change in length divided by the original length:
Strain=ΔLL0
where ΔL is the change in length and L0 is the original length.
According to Hooke's Law, stress is directly proportional to strain within the elastic limit of a material:
Stress=E×Strain
where E is Young's modulus of the material. This relationship indicates that stress must occur before strain can be measured.
From the analysis, we conclude that stress arises first when a force is applied to a material, which then leads to the generation of strain as a result of that stress. Therefore, stress precedes strain in the process of deformation.
Stress arises first, followed by strain.
Similar Questions
Knowledge Check
According to Hooke's law of elasticity, if stress is increaed, the ratio of stress to strain
AdecreasesBincreasesCbecomes zeroDremains constant
Statement-1: Elasticity restoring forces may be conservative.
Statement-2: The value of strain for same stress are different while increasing the load and while decreasing the load.
View SolutionAssertion Upto the elastic limit, strain ∝ stress.
Reason Upto elastic limit, material returns to its original shape and size, when external force is removed.
View SolutionOn gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress ∝ strain or, Stressstrain = a constant for the material of wire.
If StressStrain is x in elastic region and y in the region of yield , then

View SolutionOn gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress prop strain or, Stressstrain = a constant for the material of wire.
Just on crossing the yield region, the material will have
View SolutionOn gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress ∝ strain or, Stressstrain = a constant for the material of wire.
Two wires of same material have length and radius (L,r) and (2L,r2). The ratio of their young's modulii is

View SolutionAssertion : steel is more elastic than rubber.
Reason : For same strain , steel requires more stress to be produced in it.
View SolutionThe stress versus strain graphs for wires of two materials A and B are as shown in the figure. If YAandYB are the younng's moduli of the materials, then
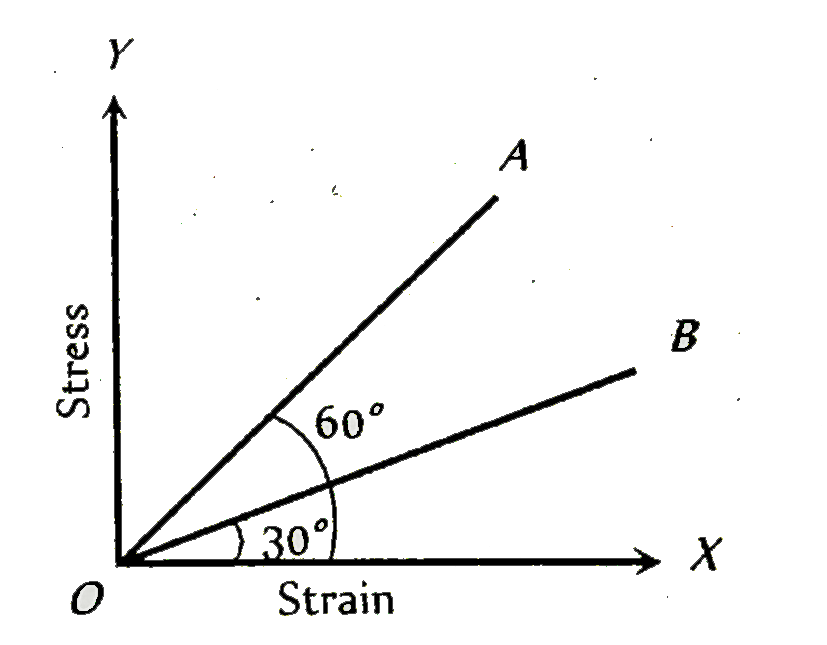
View Solution
