The speed of electromagnetic waves in vacuum is -
(A) √∈0μ0
(B) 1/√μ0∈0
(C) ∈0μ0
(D) 1/(∈0μ0)
1√μ0ε0
√μ0ε0
μ0ε0
1μ0ε0
The correct Answer is:A
To find the speed of electromagnetic waves in vacuum, we can use the relationship between the permittivity of free space (ε₀) and the permeability of free space (μ₀). The speed of electromagnetic waves (c) in vacuum is given by the formula:
c=1√ϵ0μ0
1. Understand the Constants:
- ε₀ (epsilon naught) is the permittivity of free space.
- μ₀ (mu naught) is the permeability of free space.
2. Write the Formula for Speed:
- The speed of electromagnetic waves in vacuum is expressed as:
c=1√ϵ0μ0
3. Analyze the Options:
- We need to compare this expression with the given options:
- (A) √ϵ0μ0
- (B) 1√μ0ϵ0
- (C) ϵ0μ0
- (D) 1ϵ0μ0
4. Identify the Correct Option:
- From the formula c=1√ϵ0μ0, we can see that this matches option (B) 1√μ0ϵ0.
5. Conclusion:
- Therefore, the correct answer is option (B).
- ε₀ (epsilon naught) is the permittivity of free space.
- μ₀ (mu naught) is the permeability of free space.
- The speed of electromagnetic waves in vacuum is expressed as:
c=1√ϵ0μ0
- We need to compare this expression with the given options:
- (A) √ϵ0μ0
- (B) 1√μ0ϵ0
- (C) ϵ0μ0
- (D) 1ϵ0μ0
- From the formula c=1√ϵ0μ0, we can see that this matches option (B) 1√μ0ϵ0.
- Therefore, the correct answer is option (B).
Similar Questions
In SI units, the dimensions of √ε0μ0 is:
View SolutionIn SI units, the dimensions of √ε0μ0 is
View SolutionDimension of (1μ0ɛ0) is
View SolutionThe velocity of electromagnetic radiation in a medium of permittivity ε0 and permeability μ0 is given by:
View SolutionThe dimensions of ε0μ0 are
View SolutionIf μ is the permeability and ∈ is the permittivity then 1√μ∈ is equal to
View SolutionThe dimensions of μ0 are
View Solutionif E=E0sin(kz−ωt) and B=B0(kz−ωt) are electric and magnetic field produced by an electromagnetic wave travelling in +z direction in a medium. Then if η=E0B0, then the value of η is [μ=permeability of a medium ε=permittivity of medium]
View SolutionA ray hits the y-axis making an angle θ with y-axis as shown in the figure. The variation of refractive index with x-coordinate is μ=μ0(1−xd) for 0≤x≤d(1−1μ0) and μ=μ0 for x<0, where d is a positive constant. The maximum x-coordinate of the path traced by the ray is
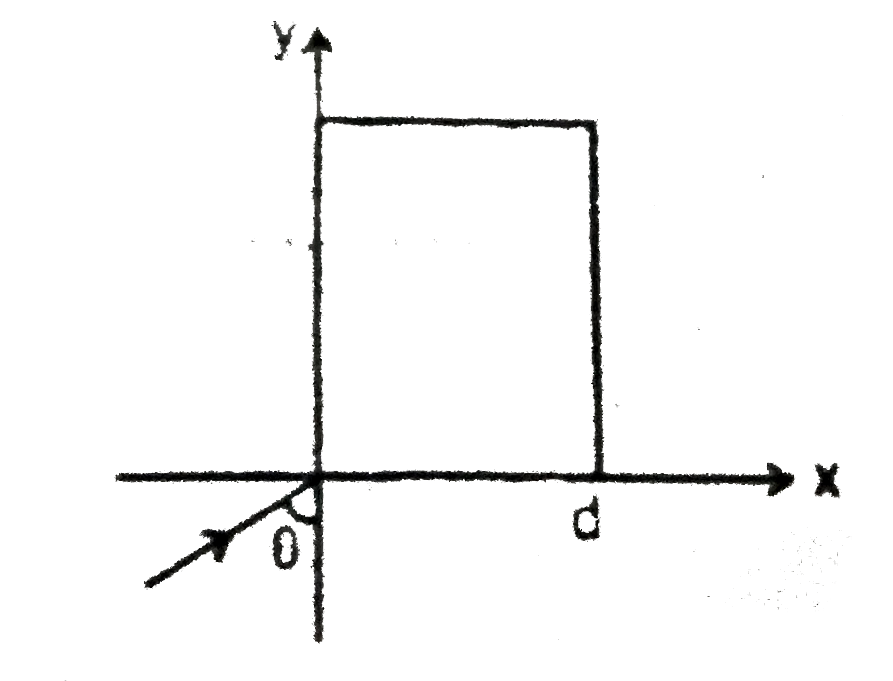
View SolutionWhich of the following can have negative value ?
A. χ
B. μr
C. μ0
D. μr and χ both
View Solution
