Match the followingColumn -IColumn -II(A)H3PO3(p)m=2.79 mol/kg(B)20 vol . of H2O2(q)M=2.31 molL−1(C)3 M NaCl solution with d=1.25gcm−3(r)1.7 mol L−1(D)Mole fraction of ethanol inH2O=0.04(s)Dibasic (t)3.4N
The correct Answer is:(A)→(s)(B)→(r,t)(C)→(p)(D)→(q)
To solve the problem of matching the items in Column I with those in Column II, we will analyze each item in Column I and determine the corresponding value from Column II step by step.
Step 1: Analyze H₃PO₃ (Phosphorous Acid)
- Basicity: H₃PO₃ has two acidic hydrogens, making it dibasic.
- Match: Therefore, H₃PO₃ corresponds to option (s) "Dibasic".
Step 2: Analyze 20 Vol. of H₂O₂ (Hydrogen Peroxide)
- Volume Strength: 20 volume means that 1 liter of H₂O₂ can release 20 liters of O₂.
- Molarity Calculation:
- Molarity (M) = Volume Strength / 11.2 = 20 / 11.2 = 1.79 mol/L (approximately).
- Normality Calculation:
- Normality (N) = Volume Strength / 5.6 = 20 / 5.6 = 3.57 N (approximately).
- Match: Therefore, 20 vol. of H₂O₂ corresponds to (r) "1.7 mol L⁻¹" and (t) "3.4 N".
Step 3: Analyze 3 M NaCl Solution with d = 1.25 g/cm³
- Density: Given density is 1.25 g/cm³, which is equivalent to 1.25 g/mL.
- Weight of Solution: For 1 L of solution, the weight = 1 L × 1.25 g/mL = 1250 g.
- Weight of Solute: Molarity (3 M) means there are 3 moles of NaCl.
- Weight of NaCl = 3 moles × 58.5 g/mol = 175.5 g.
- Weight of Solvent: Weight of solvent = Weight of solution - Weight of solute = 1250 g - 175.5 g = 1074.5 g = 1.0745 kg.
- Molality Calculation:
- Molality (m) = moles of solute / kg of solvent = 3 moles / 1.0745 kg ≈ 2.79 mol/kg.
- Match: Therefore, this corresponds to (p) "m = 2.79 mol/kg".
Step 4: Analyze Mole Fraction of Ethanol in H₂O = 0.04
- Mole Fraction: Given mole fraction of ethanol is 0.04, thus moles of water = 1 - 0.04 = 0.96.
- Weight of Water:
- Weight of water = 0.96 moles × 18 g/mol = 17.28 g.
- Volume of Water: Volume of water = 17.28 g / 1 g/mL = 17.28 mL = 0.01728 L.
- Molarity Calculation:
- Molarity = moles of ethanol / volume of solution in L = 0.04 / 0.01728 ≈ 2.31 mol/L.
- Match: Therefore, this corresponds to (q) "M = 2.31 mol L⁻¹".
Final Matching:
- A → s (H₃PO₃ is dibasic)
- B → r (20 vol. of H₂O₂ is 1.7 mol L⁻¹)
- C → p (3 M NaCl solution has m = 2.79 mol/kg)
- D → q (Mole fraction of ethanol gives M = 2.31 mol L⁻¹)
Summary of Matches:
- A - s
- B - r
- C - p
- D - q
- Basicity: H₃PO₃ has two acidic hydrogens, making it dibasic.
- Match: Therefore, H₃PO₃ corresponds to option (s) "Dibasic".
- Volume Strength: 20 volume means that 1 liter of H₂O₂ can release 20 liters of O₂.
- Molarity Calculation:
- Molarity (M) = Volume Strength / 11.2 = 20 / 11.2 = 1.79 mol/L (approximately).
- Normality Calculation:
- Normality (N) = Volume Strength / 5.6 = 20 / 5.6 = 3.57 N (approximately).
- Match: Therefore, 20 vol. of H₂O₂ corresponds to (r) "1.7 mol L⁻¹" and (t) "3.4 N".
- Density: Given density is 1.25 g/cm³, which is equivalent to 1.25 g/mL.
- Weight of Solution: For 1 L of solution, the weight = 1 L × 1.25 g/mL = 1250 g.
- Weight of Solute: Molarity (3 M) means there are 3 moles of NaCl.
- Weight of NaCl = 3 moles × 58.5 g/mol = 175.5 g.
- Weight of Solvent: Weight of solvent = Weight of solution - Weight of solute = 1250 g - 175.5 g = 1074.5 g = 1.0745 kg.
- Molality Calculation:
- Molality (m) = moles of solute / kg of solvent = 3 moles / 1.0745 kg ≈ 2.79 mol/kg.
- Match: Therefore, this corresponds to (p) "m = 2.79 mol/kg".
- Mole Fraction: Given mole fraction of ethanol is 0.04, thus moles of water = 1 - 0.04 = 0.96.
- Weight of Water:
- Weight of water = 0.96 moles × 18 g/mol = 17.28 g.
- Volume of Water: Volume of water = 17.28 g / 1 g/mL = 17.28 mL = 0.01728 L.
- Molarity Calculation:
- Molarity = moles of ethanol / volume of solution in L = 0.04 / 0.01728 ≈ 2.31 mol/L.
- Match: Therefore, this corresponds to (q) "M = 2.31 mol L⁻¹".
- A → s (H₃PO₃ is dibasic)
- B → r (20 vol. of H₂O₂ is 1.7 mol L⁻¹)
- C → p (3 M NaCl solution has m = 2.79 mol/kg)
- D → q (Mole fraction of ethanol gives M = 2.31 mol L⁻¹)
- A - s
- B - r
- C - p
- D - q
Similar Questions
Match the following :
Column-IColumn-II(A)3s1(p)n=3(B)3p1(q)l=0(C)4s1(r)l=1(D)4d1(s)m=0(t)m=±1
View SolutionMatch the Column- I with Column- II:
Column-IColumn-II(A)0.21mCa3(PO4)2(p)Solution with highest boiling point(B)0.1mNaCl(q)Solution with van't Hoff factor greater than 1(C)0.1mglucose(r)Solution with lowest osmotic pressure(d)0.1mCaCl2(s)Solution with lowest freezing point(t)Van't Hoff factors(1+2α)
View Solution
Knowledge Check
Match the rate law given in column I with the dimensions of rate constants given in column II and mark the appropriate choice.
Column IColumn II(A)Rate=k[NH3]0(i)molL−1s−1(B)Rate=k[H2O2][I−](ii)Lmol−1s−1(C)Rate=k[CH3CHO]3/2(iii)S−1(D)Rate=k[C5H5CI](iv)L1/2mol−1/2s−1A(A) → (iv), (B) → (iii), (C ) → (ii), (D) → (i)B(A) → (i), (B) → (ii) (C ) → (iv) ,(D) → (iii)C(A) → (iii), (B) → (ii) (C ) → (i) ,(D) → (iv)D(A) → (ii), (B) → (i), (C ) → (vi), (D) → (iii)Match the column I with column II and mark the appropriate choice.
Column IColumn II(A)Borax(i)Na3AIF6(B)Inorganic benzene(ii)Na2B4O7.10H2O(C)Cryolite(iii)AI2O3.2H2O(D)Bauxite(iv)B3N3H6A(A) → (ii), (B) → (iv), (C ) → (i), (D) → (iii)B(A) → (i), (B) → (ii), (C ) → (iii), (D) → (iv)C(A) → (ii), (B) → (iii), (C ) → (i), (D) → (vi)D(A) → (iii), (B) → (i), (C ) → (ii), (D) → (iv)
Match Column - I with Column - II
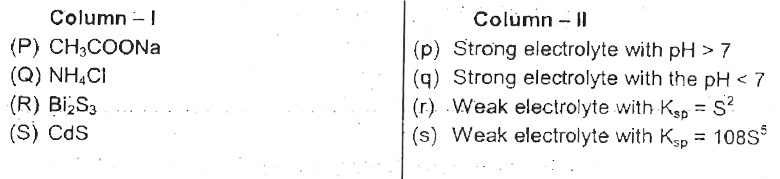
PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionThe volume strength of 2MH2O2 is (Molar mass of H2O2=34gmol−1)
View SolutionThe volume strength of g1 M H2O2 is : (Molar mass of H2O2=34gmol−1)
View SolutionThe volume strength of 1 M H2O2 is : (Molar mass of H2O2=34gmol−1
View SolutionColumn IColumn II(A)Electrical resistance(p)[M−1L−2T4A2](B)Capacitance(q)[ML2T−2A−2](C)Magnetic field(r)[ML2T−3A−2](D)Inductance(s)[MT−2A−1]
View SolutionColumn I(Oxy acids of phosphoros)Column II(Characteristic bonds)(A)H4P2O7(p)P−Pbond(s)(B)H4P2O5(q)P−O−Pbond(s)(C)H4P2O6(r)P−Hbond(s)(D)(HPO3)n(cyclic)(s)Three P-OHbonds
View Solution
