Which of the following is/are correct form of Heisenberg's indeterminacy principle?
Δp×Δx≥h2
Δv×Δx≥h2m
ΔE×Dηt≥h2
Δp×ΔE≥h2m
The correct Answer is:A, B, C
To solve the question regarding the correct forms of Heisenberg's indeterminacy principle, we will go through the key concepts and equations step by step.
Step 1: Understanding Heisenberg's Uncertainty Principle
The Heisenberg Uncertainty Principle states that there is a fundamental limit to the precision with which certain pairs of physical properties, such as position and momentum, can be known simultaneously. Mathematically, it is expressed as:
Δx⋅Δp≥h4π
where:
- Δx is the uncertainty in position,
- Δp is the uncertainty in momentum,
- h is Planck's constant.
Step 2: Relating Momentum to Velocity
Momentum (p) can be expressed in terms of mass (m) and velocity (v):
p=mv
Thus, the uncertainty in momentum can be expressed as:
Δp=m⋅Δv
where Δv is the uncertainty in velocity.
Step 3: Substituting into the Uncertainty Principle
Substituting Δp into the uncertainty principle gives:
Δx⋅(m⋅Δv)≥h4π
This can be rearranged to show that:
m⋅Δv⋅Δx≥h4π
Step 4: Energy-Time Uncertainty Relation
Another form of the uncertainty principle relates energy and time. The uncertainty in energy (ΔE) and the uncertainty in time (Δt) can be expressed as:
ΔE⋅Δt≥h4π
Step 5: Summary of Forms
From the above steps, we can summarize the forms of Heisenberg's uncertainty principle as follows:
1. Δx⋅Δp≥h4π
2. m⋅Δv⋅Δx≥h4π
3. ΔE⋅Δt≥h4π
Conclusion
The correct forms of Heisenberg's indeterminacy principle include the relationships between uncertainties in position and momentum, as well as energy and time.
The Heisenberg Uncertainty Principle states that there is a fundamental limit to the precision with which certain pairs of physical properties, such as position and momentum, can be known simultaneously. Mathematically, it is expressed as:
- Δx is the uncertainty in position,
- Δp is the uncertainty in momentum,
- h is Planck's constant.
Momentum (p) can be expressed in terms of mass (m) and velocity (v):
Substituting Δp into the uncertainty principle gives:
Another form of the uncertainty principle relates energy and time. The uncertainty in energy (ΔE) and the uncertainty in time (Δt) can be expressed as:
From the above steps, we can summarize the forms of Heisenberg's uncertainty principle as follows:
2. m⋅Δv⋅Δx≥h4π
3. ΔE⋅Δt≥h4π
The correct forms of Heisenberg's indeterminacy principle include the relationships between uncertainties in position and momentum, as well as energy and time.
Similar Questions
Knowledge Check
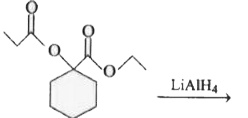
Which of the following will not form?A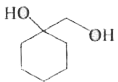 B
B C
C D
D
Which of the following is correct about Hardy Weinberg's principle ?
View SolutionThe formula for Heisenberg's uncertainty principle is
View SolutionWhich of the following forms hydrate?
View SolutionWhich of the following is the most correct expression for Heisenberg's uncerainty principle?
View SolutionWhich of the following form alkynide ?
View SolutionWhich of the following is formed in nucleolus
View SolutionIn which of the following Pollinia are formed ?
View Solution
