In a 3 dimensional space, two particles are moving with uniform speeds of 6m/s and 8m/s along two arbitrary curves. The speed of one particle, as observed by other can be :
zero
15m/s
13m/s
depends upon the actual shape of curves and the locations of two particles at some instant.
The correct Answer is:C
To solve the problem of finding the speed of one particle as observed by the other in a 3-dimensional space, we can use the concept of relative velocity.
1. Identify the Speeds of the Particles:
Let the speed of particle A be vA=6m/s and the speed of particle B be vB=8m/s.
2. Understand Relative Velocity:
The speed of one particle as observed by the other can be calculated using the formula for relative velocity. If two objects are moving with velocities →vA and →vB, the relative velocity of A with respect to B is given by:
→vAB=→vA−→vB
3. Magnitude of Relative Velocity:
The magnitude of the relative velocity can be calculated using the formula:
vAB=|→vAB|=|→vA−→vB|
Since the particles are moving along arbitrary curves, we need to consider the angle θ between their paths.
4. Using the Law of Cosines:
The magnitude of the relative velocity can also be expressed using the law of cosines:
vAB=√v2A+v2B−2vAvBcosθ
where θ is the angle between the directions of the two velocities.
5. Calculate the Range of Possible Speeds:
- If the particles are moving in the same direction (θ=0):
vAB=|vA−vB|=|6−8|=2m/s
- If the particles are moving in opposite directions (θ=180∘):
vAB=vA+vB=6+8=14m/s
- For any angle θ between 0 and 180∘, the speed of one particle as observed by the other can vary between 2m/s and 14m/s.
Conclusion:
The speed of one particle as observed by the other can vary from a minimum of 2m/s to a maximum of 14m/s.
Let the speed of particle A be vA=6m/s and the speed of particle B be vB=8m/s.
The speed of one particle as observed by the other can be calculated using the formula for relative velocity. If two objects are moving with velocities →vA and →vB, the relative velocity of A with respect to B is given by:
→vAB=→vA−→vB
The magnitude of the relative velocity can be calculated using the formula:
vAB=|→vAB|=|→vA−→vB|
Since the particles are moving along arbitrary curves, we need to consider the angle θ between their paths.
The magnitude of the relative velocity can also be expressed using the law of cosines:
vAB=√v2A+v2B−2vAvBcosθ
where θ is the angle between the directions of the two velocities.
- If the particles are moving in the same direction (θ=0):
vAB=|vA−vB|=|6−8|=2m/s
- If the particles are moving in opposite directions (θ=180∘):
vAB=vA+vB=6+8=14m/s
- For any angle θ between 0 and 180∘, the speed of one particle as observed by the other can vary between 2m/s and 14m/s.
The speed of one particle as observed by the other can vary from a minimum of 2m/s to a maximum of 14m/s.
Similar Questions
Two particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:
 View Solution
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
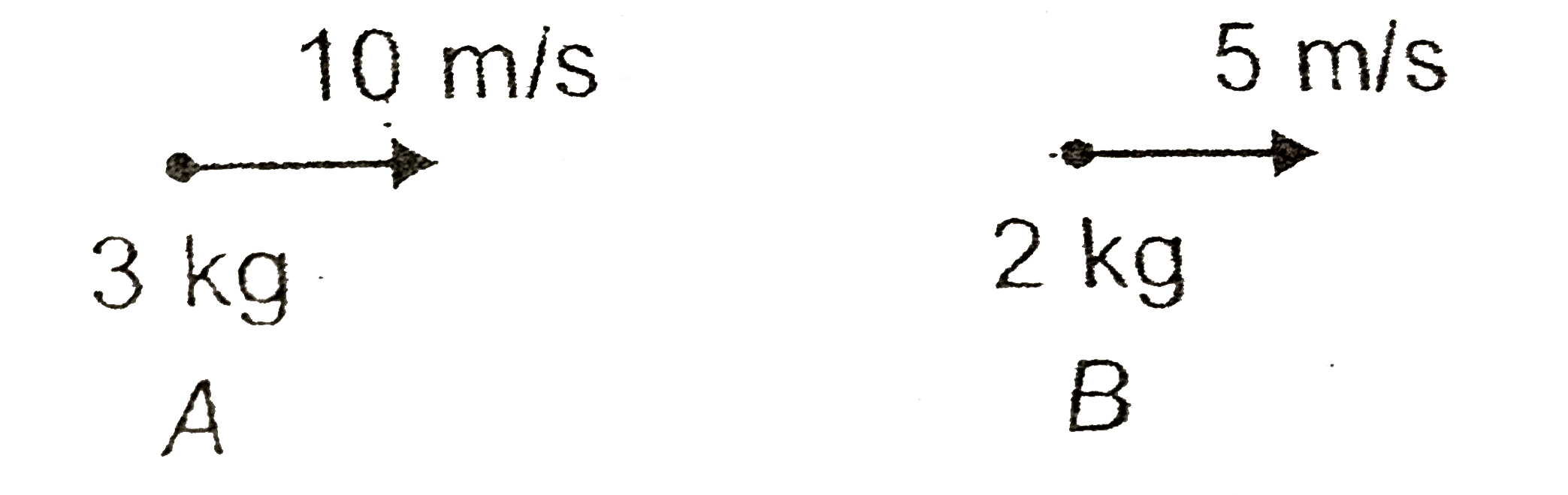
Kinetic energy of particle A when particle B has the maximum momentumView Solutionsix particles are situated at the corners of a regular hexagon. These particles start moving with equal speed of 10 m/s in such that velocity of any one particle is directed towards the next particle. Find the rate (in m/s) at which length of a side of the hexagon is decreasing.
View SolutionA particle moves in a straight line with constant speed of 4m/s for 2s, then with 6m/s for 3s. Find the average speed of the particle in the given time interval.
View SolutionA particle moving in a straight line covers half the distance with speed of 3m/s. The half of the distance is covered in two equal intervals with speed of 4.5m/sand7.5m/s respectively. The average speed of the particle during this motion is :
View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA particle moves with a uniform velocity of 50 m/s for 20 min. What is the velocity of particle at t = 2 min ?
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
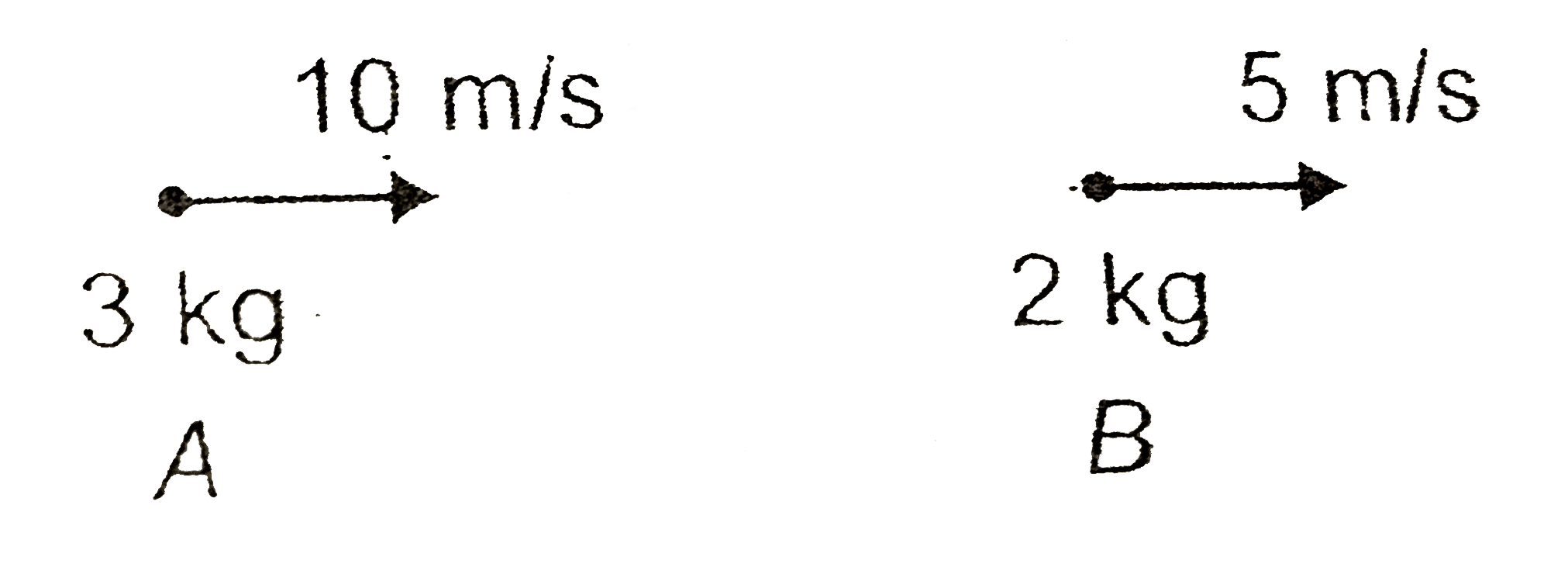
Find the maximum momentum that particle B can have after collision with AView SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
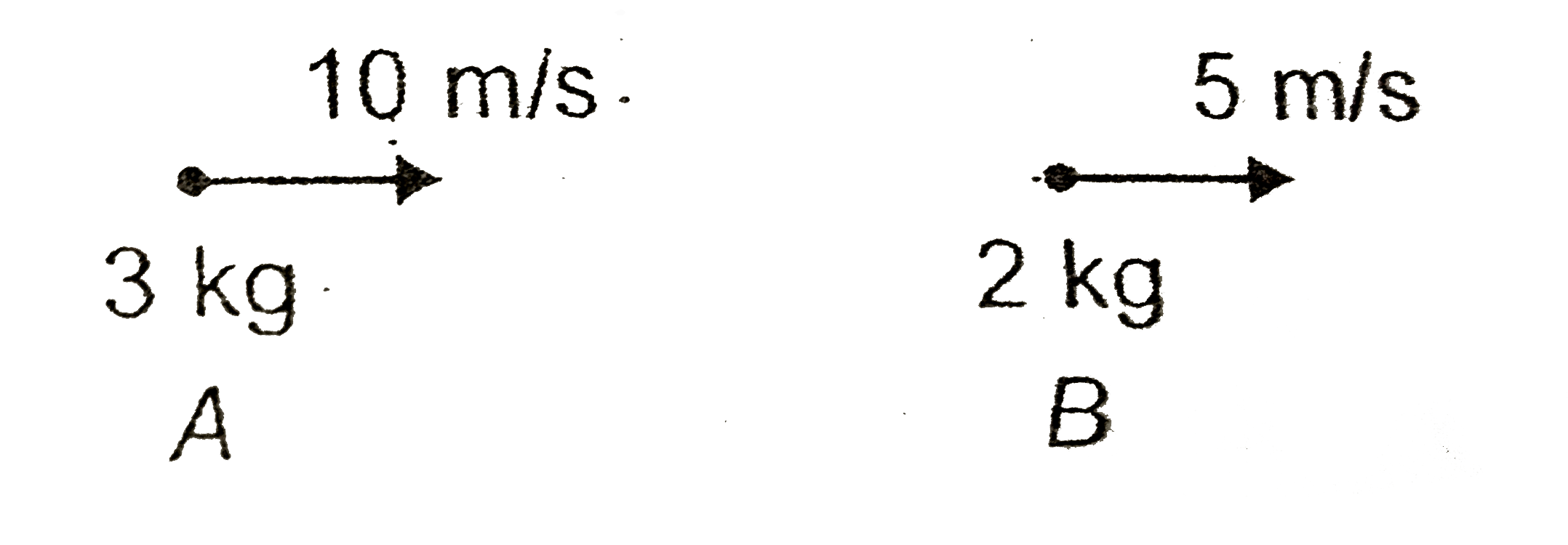
Find the maximum momentum that particles A can have after collision with B.View Solution

